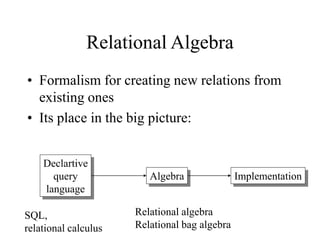
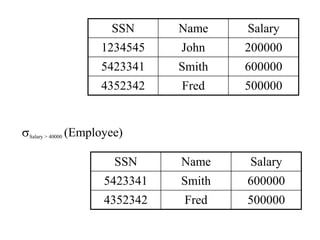
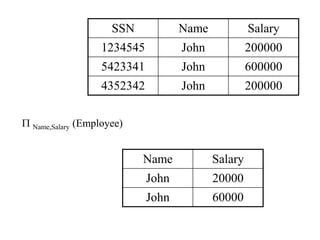
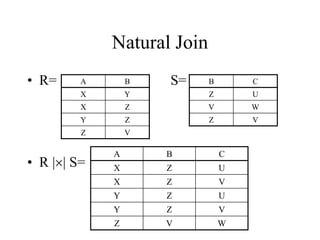
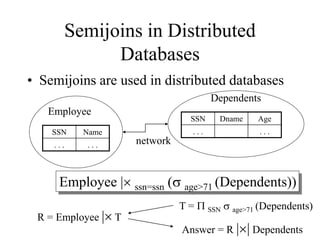
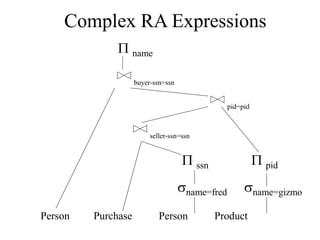
The document discusses relational algebra, which is a formalism for creating new relations from existing ones. It describes the five basic relational algebra operators - union, difference, selection, projection, and cartesian product. It also covers derived operators like intersection, joins (natural, equi-join, theta join, semi-join), and renaming. Examples are provided to illustrate each operator. Relational algebra is used to translate SQL queries into optimized execution plans.

1. Relational Algebra
IN DBMS

2. DBMS Architecture
How does a SQL engine work ?
• SQL query  relational algebra plan
• Relational algebra plan  Optimized plan
• Execute each operator of the plan

3. Relational Algebra
• Formalism for creating new relations from
existing ones
• Its place in the big picture:
Declartive
query
language
Algebra Implementation
SQL,
relational calculus
Relational algebra
Relational bag algebra

4. Relational Algebra
• Five operators:
– Union: 
– Difference: -
– Selection: s
– Projection: P
– Cartesian Product: 
• Derived or auxiliary operators:
– Intersection, complement
– Joins (natural,equi-join, theta join, semi-join)
– Renaming: r

5. 1. Union and 2. Difference
• R1  R2
• Example:
– ActiveEmployees  RetiredEmployees
• R1 – R2
• Example:
– AllEmployees -- RetiredEmployees

6. What about Intersection ?
• It is a derived operator
• R1  R2 = R1 – (R1 – R2)
• Also expressed as a join (will see later)
• Example
– UnionizedEmployees  RetiredEmployees

7. 3. Selection
• Returns all tuples which satisfy a condition
• Notation: sc(R)
• Examples
– sSalary > 40000 (Employee)
– sname = “Smith” (Employee)
• The condition c can be =, <, , >, , <>

8. sSalary > 40000 (Employee)
SSN Name Salary
1234545 John 200000
5423341 Smith 600000
4352342 Fred 500000
SSN Name Salary
5423341 Smith 600000
4352342 Fred 500000

9. 4. Projection
• Eliminates columns, then removes duplicates
• Notation: P A1,…,An (R)
• Example: project social-security number and
names:
– P SSN, Name (Employee)
– Output schema: Answer(SSN, Name)

10. P Name,Salary (Employee)
SSN Name Salary
1234545 John 200000
5423341 John 600000
4352342 John 200000
Name Salary
John 20000
John 60000

11. 5. Cartesian Product
• Each tuple in R1 with each tuple in R2
• Notation: R1  R2
• Example:
– Employee  Dependents
• Very rare in practice; mainly used to express
joins

12. Cartesian Product Example
Employee
Name SSN
John 999999999
Tony 777777777
Dependents
EmployeeSSN Dname
999999999 Emily
777777777 Joe
Employee x Dependents
Name SSN EmployeeSSN Dname
John 999999999 999999999 Emily
John 999999999 777777777 Joe
Tony 777777777 999999999 Emily
Tony 777777777 777777777 Joe

13. Relational Algebra
• Five operators:
– Union: 
– Difference: -
– Selection: s
– Projection: P
– Cartesian Product: 
• Derived or auxiliary operators:
– Intersection, complement
– Joins (natural,equi-join, theta join, semi-join)
– Renaming: r

14. Renaming
• Changes the schema, not the instance
• Notation: r B1,…,Bn (R)
• Example:
– rLastName, SocSocNo (Employee)
– Output schema:
Answer(LastName, SocSocNo)

15. Renaming Example
Employee
Name SSN
John 999999999
Tony 777777777
LastName SocSocNo
John 999999999
Tony 777777777
rLastName, SocSocNo (Employee)

16. Natural Join
• Notation: R1 || R2
• Meaning: R1 || R2 = PA(sC(R1  R2))
• Where:
– The selection sC checks equality of all common
attributes
– The projection eliminates the duplicate common
attributes

17. Natural Join Example
Employee
Name SSN
John 999999999
Tony 777777777
Dependents
SSN Dname
999999999 Emily
777777777 Joe
Name SSN Dname
John 999999999 Emily
Tony 777777777 Joe
Employee Dependents =
PName, SSN, Dname(s SSN=SSN2(Employee x rSSN2, Dname(Dependents))

18. Natural Join
• R= S=
• R || S=
A B
X Y
X Z
Y Z
Z V
B C
Z U
V W
Z V
A B C
X Z U
X Z V
Y Z U
Y Z V
Z V W

19. Natural Join
• Given the schemas R(A, B, C, D), S(A, C, E),
what is the schema of R || S ?
• Given R(A, B, C), S(D, E), what is R || S ?
• Given R(A, B), S(A, B), what is R || S ?

20. Theta Join
• A join that involves a predicate
• R1 || q R2 = s q (R1  R2)
• Here q can be any condition

21. Eq-join
• A theta join where q is an equality
• R1 || A=B R2 = s A=B (R1  R2)
• Example:
– Employee || SSN=SSN Dependents
• Most useful join in practice

22. Semijoin
• R | S = P A1,…,An (R || S)
• Where A1, …, An are the attributes in R
• Example:
– Employee | Dependents

23. Semijoins in Distributed
Databases
• Semijoins are used in distributed databases
SSN Name
. . . . . .
SSN Dname Age
. . . . . .
Employee
Dependents
network
Employee | ssn=ssn (s age>71 (Dependents))
T = P SSN s age>71 (Dependents)
R = Employee | T
Answer = R || Dependents

24. Complex RA Expressions
Person Purchase Person Product
sname=fred sname=gizmo
P pid
P ssn
seller-ssn=ssn
pid=pid
buyer-ssn=ssn
P name

25. Operations on Bags
A bag = a set with repeated elements
All operations need to be defined carefully on bags
• {a,b,b,c}{a,b,b,b,e,f,f}={a,a,b,b,b,b,b,c,e,f,f}
• {a,b,b,b,c,c} – {b,c,c,c,d} = {a,b,b,d}
• sC(R): preserve the number of occurrences
• PA(R): no duplicate elimination
• Cartesian product, join: no duplicate elimination
Important ! Relational Engines work on bags, not sets !
Reading assignment: 5.3 – 5.4

26. Finally: RA has Limitations !
• Cannot compute “transitive closure”
• Find all direct and indirect relatives of Fred
• Cannot express in RA !!! Need to write C program
Name1 Name2 Relationship
Fred Mary Father
Mary Joe Cousin
Mary Bill Spouse
Nancy Lou Sister