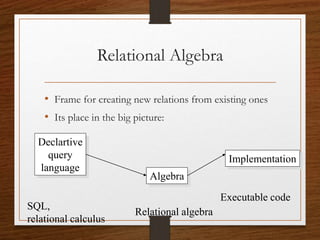
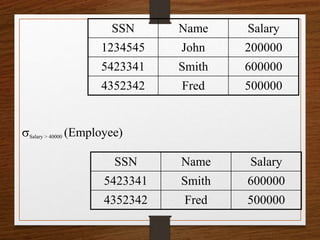
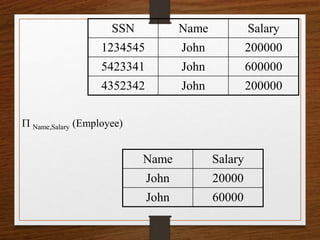
Relational algebra is a procedural query language used to manipulate data in relational databases. It consists of five basic operators: union, difference, selection, projection, and Cartesian product. Additional derived operators include intersection, complement, and various join operations. Relational algebra provides a theoretical foundation for relational databases and sits between declarative query languages like SQL and the implementation code in a DBMS that executes queries.