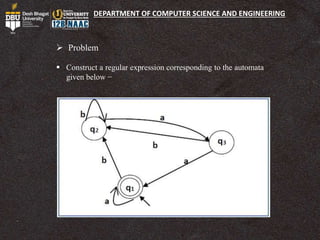
The document discusses regular expressions and their properties. It begins with defining regular expressions recursively and provides examples. It then discusses properties of regular sets such as their unions, intersections, complements being regular. It also discusses identities related to regular expressions and proves Arden's theorem. Finally, it solves a problem to find the regular expression for a given automaton using Arden's theorem.












![DEPARTMENT OF COMPUTER SCIENCE AND ENGINEERING
Statement −
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution that is R
= QP*
Arden's Theorem
Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following
equation −
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]
Hence, proved.](https://image.slidesharecdn.com/rohitautoppt-230203045259-ec24692c/85/regular-expression-13-320.jpg)