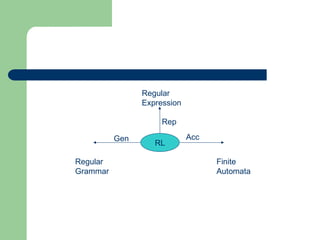
The document explains the relationship between regular expressions, finite automata, and regular grammars. It outlines how to construct non-deterministic finite automata (NFA) and deterministic finite automata (DFA) from regular expressions, and illustrates various examples of regular expressions over a binary alphabet. Additionally, it details the identities and precedence of regular expression operators.

1. RL
Finite
Automata
Regular
Grammar
Regular
Expression
Acc
Gen
Rep

2. Regular Expressions
 A regular expression is used to specify a
language
 Given a regular expression, NFA, DFA can
be constructed
 Let Σ be an alphabet. The regular
expressions over Σ are:
– Ø Represents the empty set { }
– ε Represents the set {ε}
– a Represents the set {a}, for any symbol a in Σ

3.  Let r and s be regular expressions that
represent the sets R and S, respectively.
– r+s Represents the set R U S
– rs Represents the set RS
– r* Represents the set R*
– (r) Represents the set R
If r is a regular expression, then L(r) is used to
denote the corresponding language

4. Examples: Let Σ = {0, 1}
(0 + 1)* All strings of 0’s and 1’s
0(0 + 1)* All strings of 0’s and 1’s, beginning with a 0
(0 + 1)*1 All strings of 0’s and 1’s, ending with a 1
(0 + 1)*0(0 + 1)* All strings of 0’s and 1’s containing at least one 0
(0 + 1)*0(0 + 1)*0(0 + 1)* All strings of 0’s and 1’s containing at
least two 0’s
(0 + 1)*01*01* All strings of 0’s and 1’s containing at least two 0’s
(1 + 01*0)* All strings of 0’s and 1’s containing an even
number of 0’s
1*(01*01*)* All strings of 0’s and 1’s containing an even
number of 0’s
(1*01*0)*1* All strings of 0’s and 1’s containing an even
number of 0’s

5. Identities:
Øu = uØ = Ø Multiply by 0
εu = uε = u Multiply by 1
Ø* = ε
ε* = ε
u+v = v+u
u + Ø = u
u + u = u
u* = (u*)*
u(v+w) = uv+uw
(u+v)w = uw+vw
(uv)*u = u(vu)*
(u+v)* = (u*+v)* = u*(u+v)*= (u+vu*)*= (u*v*)*= u*(vu*)*= (u*v)*u*

6. The precedence of the RE
operators
 The star “*” operator takes the highest
precedence
 Next in precedence comes the
concatenation/ “dot” operator
 Finally, all unions “+” are grouped with their
operands

7. Finite automata and Regular
expressions
 Every language defined by one of the
automata is also defined by a regular
expression
 Every language defined by a regular
expression is defined by one of the automata