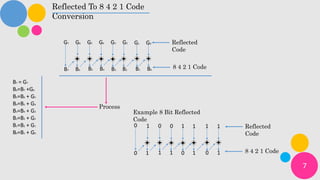
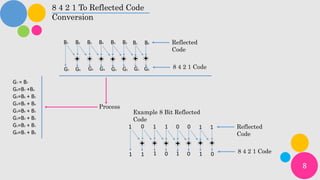
This document discusses reflected code and the conversion between reflected code and 8-4-2-1 binary code. It provides a brief history of binary code and reflected code. Reflected code, also known as Gray code, involves only a single bit changing between adjacent values. The document shows how to convert between 8-bit reflected code and 8-4-2-1 binary code using addition rules. Examples of both conversions are provided.

1. Reflected code and conversion among
reflected code and 8 4 2 1 binary code
Saumya Som
BWU/BCA/17/207
BCA-D(1st Semester)
Teacher- SOUMIK GUHA ROY

2. Table of
Contents
Binary code
History Of Binary Code
Reflected Code
Reflected To 8 4 2 1 Code Conversion
8 4 2 1 To Reflected Code Conversion
History Of Reflected Code

3. Binary code
Binary code is the simplest form of computer code or programming
data. It is represented entirely by a binary system of digits consisting
of a string of ‘0’ and ‘1’.
The code is known as 8-4-2-1 code. This is because 8, 4, 2, and 1 are
the weights of the fours bits of the BCD code
1

4. History Of Binary
Code
167
9
The modern binary number system, the basis for
binary code, was invented by Gottfried Leibniz in
1679 and appears in his article Explication de
l'Arithmétique Binaire. which uses only the
characters 1 and 0
2
184
7
Another mathematician and philosopher by
the name of George Boole published a paper
in 1847 called 'The Mathematical Analysis
of Logic' that describes an algebraic system
of logic, now known as Boolean algebra

5. Example of Binary Cody In Decimal
System
0
1
4
3
2
5
6
7
8
9
10
11
12
13
14
15
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
Example - (15)10 =
(?)2
Answer - (15)10 =
(1111)2
Rule : Even Number – Put ‘0’
Odd Number – Put ‘1’
3
15731
2 22
1111
Count Left To
Right

6. Reflected
CodeThis is a variable weighted code and is cyclic. This
means that if it is arranged so that every transition
form one value to the nest value involves only one bit
change . The gray code is sometimes referred to as
reflected binary code, because the first eight values
compare with those of the last 8 values, but in
reverse order
24

7. 1947
Reflected Binary
CodeBell Labs researcher Frank
Gray introduced the
term reflected binary code
1953
Gray Code
The code was later named
after Gray by others who
used it. Two different 1953
patent applications give
"Gray code" as an alternative
name for the "reflected binary
code
History Of Reflected
Code
5

8. 15
14
13
12
11
10
9
8 1 0 0
1 0 1
1 1 1
1 1 0
0 1 0
0 1 1
0 0 1
0 0 0
7
6
5
4
3
2
1
0 0 0 0
0 0 1
0 1 1
0 1 0
1 1 0
1 1 1
1 0 1
1 0 0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
6
15
14
13
12
11
10
9
8 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
7
6
5
4
3
2
1
0 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Reflected
Code
Binary
code

9. 7
Reflected To 8 4 2 1 Code
Conversion
G7 G6 G4 G0G1G2G5 G3
B7 B1B2B3B4B5B6 B0
B7 = G7
B6=B7 +G6
B5=B6 + G5
B4=B5 + G4
B3=B4 + G3
B2=B3 + G2
B1=B2 + G1
B0=B1 + G0
Example 8 Bit Reflected
Code
Reflected
Code
8 4 2 1 Code
0 1 0 1110 1
0 010111 1
Reflected
Code
8 4 2 1 Code
Process

10. 8
8 4 2 1 To Reflected Code
Conversion
B7 B6 B4 B0B1B2B5 B3
G7 G1G2G3G4G5G6 G0
G7 = B7
G6=B7 +B6
G5=B6 + B5
G4=B5 + B4
G3=B4 + B3
G2=B3 + B2
G1=B2 + B1
G0=B1 + B0
Example 8 Bit Reflected
Code
Reflected
Code
8 4 2 1 Code
Process
1 0 1 1101 0
1 101011 0
Reflected
Code
8 4 2 1 Code