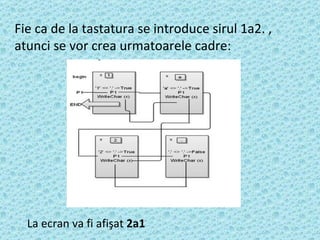
Documentul prezintă conceptul de recursivitate în programare, explicând definiția și importanța acesteia în rezolvarea problemelor complexe. Recursivitatea este definită prin subprograme care se autoapelează, iar documentul detaliază tipurile de recursivitate: directă și indirectă. Un exemplu ilustrativ al utilizării recursivității este calcularea factorialului unui număr natural.

1. MATERIAL DIDACTIC PENTRU STUDEN Ţ I LA DISCIPLINA “BAZELE PROGRAM Ă RII ” RECURSIVITATE Elaborat : Bacalîm Alina studentă la USB “Alecu Russo” 10. 01 .201 1 desktop: recursie .ppt

2. Recursivitatea repre zintă o tehnică de programare de o importanţă deosebită. Ea permite o exprimare extrem de concisă şi clară a algoritmilor de rezolvare a unor probleme complexe. În matematică, o noţiune este definită recursiv dacă în cadrul definiţiei apare noţiunea care se defineşte.

3. D efiniţia recursivă a factorialului unui număr natural n este: 1, dacă n =0 n! = n *(n-1)! , dacă n >0 Exemplu: 5! = 5*4! = 5*4*3! = 5*4*3*2! = 5*4*3*2*1! = 5*4*3*2*1*0! = 120

4. În programare, recursivitatea se exprimă cu ajutorul subprogramelor , deoarece ele se identifică printr-un nume care este apoi specificat apoi în apeluri. Un subprogram este recursiv dacă se autoapelează .

5. Dacă apelul subprogramului apare chiar în corpul său, recursivitatea se numeşte directă . Iar dacă apelul subprogramului recursiv apare în corpul unui alt subprogram care se apelează direct sau indirect din subprogramul recursiv, recursivitatea se numeşte indirectă .

6. Un subprogram este activ de la apelul său până la revinirea în subprogramul apelant. Subprogramul rămîne activ, chiar dacă din cadrul său se activează alte subprograme. Astfel, se poate spune, că un subprogram este recursiv dacă apelul său apare când subprogramul este activ.

7. Executarea unei proceduri nerecursive P1 care apelează o altă procedură nerecursivă P2 constă în: - executarea secvenţei de început a procedurii P1 care precede apelul procedurii P2 ; - executarea procedurii P2 : - executarea secvenţei de sfârşit a procedurii P1 .

8. Schema generală a unei proceduri recursive:

9. Procedure P1 Var X: Char Begin ReadChar(X) If X <> ‘.’ Then P1 End WriteChar(X) End Begin P1 END. Exemplu rezolvat

10. Fie ca de la tastatura se introduce sirul 1a2. , atunci se vor crea urmatoarele cadre: La ecran va fi afi şat 2a1

11. SF ÎRŞIT