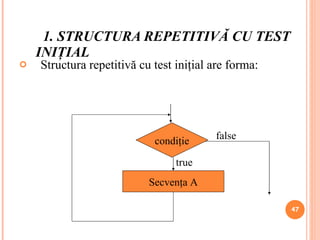
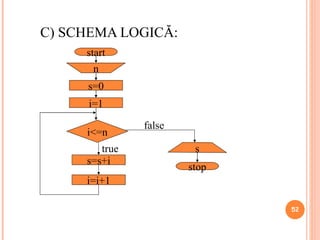
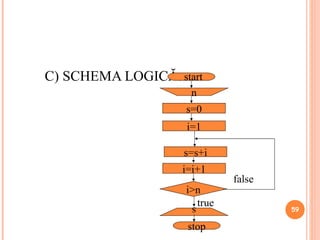
Documentul oferă o introducere în algoritmi, definiția acestora și exemplificări prin metode de rezolvare a problemelor matematice. Prezentarea se concentrează pe diferite structuri de control (secvență, decizie, repetiție) și pe metodele de reprezentare a algoritmilor, cum ar fi pseudocodul și schemele logice. De asemenea, se includ teme și aplicații pentru a consolida conceptele discutate.

1. CLUBUL COPIILOR VISEU DE SUS MARAMURES prof. RalucaMaria Moldovan Algoritmi

2. N OŢIUNI INTRODUCTIVE DEFINIRE EXEMPLE DIN MATEMATICĂ METODE DE REPREZENTARE LIMBAJ PSEUDOCOD SCHEME LOGICE STRUCTURI FUNDAMENTALE DE CONTROL STRUCTURA LINIARĂ STRUCTURA DECIZIONALĂ STRUCTURA REPETITIVĂ APLICAŢII Din Cuprins:

3. NOŢIUNI INTRODUCTIVE Pentru a înţelege noţiunea de algoritm vom porni de la un exemplu. EX: Să presupunem că mama ne roagă să cumpărăm pâine. Ce trebuie să facem?

4. Când am decis să plecăm la maga z in vom proceda astfel: - luăm banii necesari; - ne îndreptăm către magazin; - solicităm o pâine; - o plătim; - venim cu ea către casă; - o dăm mamei.

5. Am obţinut astfel un algoritm : * care conţine 6 etape (deci un număr finit de operaţii); * care au fost scrise în ordinea în care trebuie executate (deci sunt ordonate); * fiecare etapă este explicată în cuvinte (deci este complet definită); * şi care pornind de la ceva (în cazul nostru bani) obţinem ceea ce dorim (pâinea).

6. DEF: Se numeşte algoritm o secvenţă finită de operaţii ordonată şi complet definită care pornind de la datele de intrare produce rezultatele. Putem defini acum noţiunea de algoritm sintetizând cele spuse astfel:

7. Un alt exemplu : Presupunem că vrem să citim un număr întreg (pe care noi îl introducem de la tastatură) şi îl tipărim (pe ecranul monitorului). Şirul acţiunilor ce trebuie executate este următorul: citeşte numărul tipăreşte numărul Şi în acest caz am obţinut un algoritm. Acţiunile trebuie executate în ordinea în care au fost puse. Astfel, nu putem tipări numărul înainte ca acesta să fie cunoscut (citit).

8. Temă: Scrieţi un algoritm care calculează suma a două numere întregi a şi b. Modificaţi apoi algoritmul astfel încât să calcul e ze şi produsul celor două numere.

9. Rezolvare: Algoritmul problemei: 1. Solicită valori pentru a şi b 2. Calculează S=a+b 3. Furnizează rezultatul pentru S

10. Algoritmul modificat are forma: 1. Solicită valori pentru a şi b 2. Calculează S=a+b 3. Calculează P=a*b 4. Furnizează rezultatul pentru S şi pentru P

11. Metode de reprezentare a algoritmilor Limbajul natural nu permite o descriere suficient de exactă a algoritmilor. Din acest motiv pentru reprezentarea algoritmilor se folosesc diferite forme de descriere caracteristice.

12. Două din cele mai folosite forme de descriere a algoritmilor sunt: limbajul pseudocod; Scheme logice.

13. Reprezentarea algoritmilor în limbaj pseudocod Limbajul pseudocod foloseşte cuvinte cheie, adică nişte cuvinte cu înţeles prestabilit ce indică operaţia care se execută.

14. Exemplu: Să se calculeze suma a două numere naturale a şi b. Rezolvare: a) Algoritmul: 1. Solicită valori pentru a şi b 2. Calculează S=a+b 3. Furnizează rezultatul pentru S

15. b) Pseudocodul: citeşte a,b S=a+b scrie S stop

16. Temă: Să se calculeze media aritmetică a 3 numere întregi x, y şi z. Se cer: a) algoritmul; b) pseudocodul.

17. Reprezentarea algoritmilor prin scheme logice Schemele logice utilizează săgeţi de legătură între diferite forme geometrice care simbolizează acţiunile ce urmează a fi executate. În continuare sunt prezentate blocurile care intră în componenţa unei scheme logice:

18. Bloc pentru introducerea datelor (bloc de citire) unde “Listă variabile” cuprinde numele simbolice ale variabilelor cărora li se asociază valori numerice (citite). Listă variabile

19. 2. Bloc de extragere a rezultatelor (bloc de scriere) unde variabilele menţionate în listă constituie rezultate ale problemei. Listă variabile

20. 3. Bloc de calcul (bloc de atribuire) Un astfel de bloc indică următoarea succesiune de operaţii: - se calculează expresia din membrul drept; - se atribuie variabilei din membrul stâng valoarea calculată anterior (V reprezintă numele variabilei). V = expresie

21. 4 . Bloc de deci zie (bloc decizional) Condiţia logică înscrisă poate să aibă valoarea “adevărat” sau “fals”; în funcţie de valoarea logică obţinută, blocul următor care va fi parcurs va fi legat de ramura “true”(adevărat) sau ramura “false”(fals). condiţie TRUE FALSE

22. 5 . Bloc de început (bloc de start) Indică începutul algoritmului. START

23. 6. Bloc de sfârşit (bloc de stop) Indică sfârşitul algoritmului. STOP

24. EXEMPLU: Să se calculeze suma a două numere naturale a şi b. Rezolvare : a) Algoritmul: 1. Solicită valori pentru a şi b 2. Calculează S=a+b 3. Furnizează rezultatul pentru S

25. citeşte a,b S=a+b scrie S stop b) Pseudocodul:

26. C) SCHEMA LOGICĂ: a START a, b S=a+b STOP

27. TEMĂ: Să se calculeze produsul a trei numere întregi x, y şi z. Se cer: a) algoritmul; b) pseudocodul; c) schema logică.

28. STRUCTURI DE CONTROL O structură înseamnă o combinaţie de operaţii utilizată în scrierea algoritmilor. Orice algoritm care are un punct de început şi un punct de sfârşit poate fi reprezentat ca o combinaţie a trei structuri de control: Secvenţa; Decizia; Repetiţia.

29. STRUCTURA SECVENŢIALĂ Secvenţa reprezintă o succesiune de două sau mai multe operaţii care conţine o transformare de date: în care “Secvenţa A” repre zintă o transformare de date. Secvenţa A

30. EXEMPLU: Să se calculeze suma, produsul şi diferenţa a trei nume întregi x, y şi z. algoritmul: 1. Se dau valori pentru x, y şi z 2. Calculează S=x+y+z 3. Calculează P=x*y*z 4. Calculează diferenţa D=x-y-z 5. Afişează rezultatele pentru S, P şi D.

31. b) pseudocodul: citeşte x, y, z S=x+y+z P=x*y*z D=x-y-z scrie S, P, D stop

32. c ) Schema logică: START x,y,z P=x*y*z D=x-y-z STOP S=x+y+z S, P, D

33. TEMĂ: Se dau trei numere naturale a, b şi c. Să se calculeze valorile expresiilor: S1=(a+b)*(a-b) S2=a*b+a*c+b*c P=S1*S2 Se cer: a) algoritmul; b) pseudocodul; c) schema logică.

34. STRUCTURA DECIZIONALĂ Decizia reprezintă alegerea unei operaţii sau a unei secvenţe de operaţii dintre două alternative posibile. Forma structurii decizionale este următoarea: condi ţie Secvenţa A Secvenţa B true false

35. În limbaj natural, execuţia poate fi descrisă astfel: se evalueză condiţia; dacă condiţia este adevărat, se execută “Secvenţa A”; în caz contrar (dacă condiţia este falsă) se execută “ Secvenţa B”. În pseudocod, execuţia se descrie astfel: dacă condiţie atunci Secvenţa A altfel Secvenţa B

36. EXEMPLU: Se dau două numere naturale a şi b. Să se determine care dintre ele are valoarea mai mare. Rezolvare: a) Algoritmul: Se dau valori lui a şi b Se determină maximul dintre a şi b: dacă a este mai mare ca b atunci maximul este a altfel maximul este b 3. Se afişează maximul

37. b) Pseudocodul: citeşte a dacă a >b atunci max=a altfel max=b scrie max stop

38. c) Schema logică: start stop a, b a>b max=a max=b true false max

39. TEM Ă: Să se determine dacă un număr x este pozitiv sau nu. Se cer: - algoritmul; - pseudocodul; - schema logică.

40. DECIZIA CU VARIANTA UNEI CĂI NULE Mai există o formă a structurii decizionale şi anume cea cu varianta unei căi nume. Forma acestei structuri este următoarea: condi ţie Secvenţa A true false

41. ÎN LIMBAJ NATURAL, EXECUŢIA POATE FI DESCRISĂ ASTFEL: se evalueză condiţia; dacă condiţia este adevărat, se execută “Secvenţa A” apoi execuţia structurii decizionale se încheie; în caz contrar (dacă condiţia este falsă) execuţia structurii decizionale se încheie. În pseudocod, execuţia se descrie astfel: dacă condiţie atunci Secvenţa A

42. EXEMPLU: Se citeşte o valoare întreagă a. În cazul în care aceasta este nulă (egală cu 0) se va tipări mesajul “am citit zero”. Altfel, nu se va da mesaj. Rezolvare: a) Algoritmul: Se dă valoare lui a Se determină dacă a este nul: dacă a este egal cu zero atunci se va tipări “ am citit zero”

43. b) Pseudocodul: citeşte a dacă a=0 atunci scrie ‘ am citit zero ’ stop

44. c ) Schema logică: start stop a a =0 true false ‘ am citit zero ’

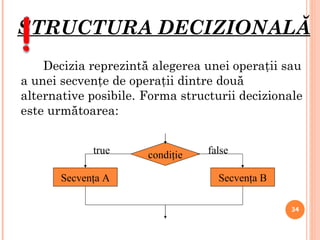
45. TEM Ă: Se citeşte de la tastatură un număr întreg x. În cazul în care acesta este cuprins în intervalul [ 1,100 ] se va afişa mesajul “număr cuprins în interval”, altfel nu se va afişa nici un mesaj. Se cer: algoritmul; pseudocodul; schima logică.

46. STRUCTURA REPETITIVĂ Repetiţia (bucla sau iteraţia) asigură execuţia unei secvenţe în mod repetat în funcţie de o anumită condiţie. Există trei tipuri de structuri repetitive: - bucla cu test iniţial; - bucla cu test final; - bucla cu contor.

47. 1. STRUCTURA REPETITIVĂ CU TEST INIŢIAL Structura repetitiv ă cu test iniţial are forma: condiţie Secvenţa A true false

48. a Execuţia structurii repetitive cu test iniţial presupune parcurgerea următoarelor etape: Se evaluează condiţia; dacă rezultatul este adevărat se trece la pasul 2, altfel execuţia se încheie; 2. Se execută secvenţa A, apoi se trece la pasul 1).

49. EXPRIMAREA ÎN PSEUDOCOD: cât timp condiţie execută Secvenţa A

50. EXEMPLU: Să se calculeze suma primelor n numere naturale. Re zolvare: a) Algoritmul: 1. Se dă valoare lui n; 2. Se dă lui S valoarea 0 şi lui I valoarea 1 3. Cât timp I este mai mic sau egal cu n se calculează suma după formula S=S+I şi I ia valoarea următorului termen al sumei, după formula I=I+1 4. Se afişează valoarea sumei S .

51. B) PSEUDOCODUL: citeşte n S=0 I=1 cât timp I <=n execut ă S=S+I I=I+1 scrie S stop

52. C) SCHEMA LOGICĂ: a start stop n s=0 i=1 s=s+i i=i+1 i<=n s false true

53. TEMĂ Să se calculeze produsul primelor n numere naturale. Se cer: a) algoritmul; b) pseudocodul; c) schema logică.

54. 2. STRUCTURA REPETITIVĂ CU TEST FINAL : Structura repetitivă cu test final are forma : Secvenţa A condiţie false true

55. a Execu ţia buclei cu test final presupune parcurgerea următoarelor etape: Se execută secvenţa A 2. Se evaluează condiţia; dacă rezultatul este fals, se continuă cu pasul 1), în caz contrar, se încheie execuţia buclei.

56. EXPRIMAREA ÎN PSEUDOCOD: repetă Secvenţa A până când condiţie

57. EXEMPLU: Să se calculeze suma primelor n numere naturale. Rezolvare: a) Algoritmul: 1. Se dă valoare lui n; 2. Se dă lui S valoarea 0 şi lui I valoarea 1 3. Se calculează suma după formula S=S+I şi I ia valoarea I=I+1, până când I >n . 4. Se afişează valoarea sumei.

58. B) PSEUDOCODUL: a citeşte n S=0 I=1 repetă S=S+I I=I+1 p ână când I>n scrie S stop

59. C) SCHEMA LOGIC Ă: a stop n s s=0 i=1 s=s+i i=i+1 i>n false true start

60. TEMĂ: Să se calculeze produsul primelor n numere naturale. Se cer : - algoritmul; - pseudocodul; - schema logică.

61. 3 . STRUCTURA REPETITIVĂ CU CONTOR : Structura repetitivă cu contor are forma: unde cu “vi” s-a notat valoarea iniţială, iar cu “vf” s-a notat valoarea finală. contor=vi contor < =vf false true secvenţa A contor=contor +pas

62. Această structură are un număr cunoscut de repetiţii a “Secvenţei A”, motiv pentru care se numeşte structură repetitivă cu contor. Execuţia structurii repetitive cu contor presupune parcurgerea următoarelor etape: 1). Variabila de ciclare “contor” ia valoarea iniţială “vi”. 2). Dacă “contor” este mai mic sau egal cu valoarea finală “vf”, se execută “Secvenţa A”, se adună 1 la “contor” şi se reia cu pasul 2).. Altfel, execuţia este încheiată.

63. pentru contor=vi, vf execută secvenţa A Exprimarea în pseudocod:

64. EXEMPLU: Să se calculeze suma primelor n numere naturale. Rezolvare: a) Algoritmul: 1. Se dă valoare lui n; 2. Se dă lui S valoarea 0 şi lui I valoarea 1 3. Pentru I luând valori de la 1 până la n se calculează suma după formula S=S+I 4. Se afişează valoarea sumei.

65. B) PSEUDOCODUL : citeşte n S=0 petntru I=1, n execută S=S+I scrie S stop

66. C) SCHEMA LOGICĂ: start stop n s i=1 s=s+i i=i+1 i< = n true false s=0

67. TEMĂ: Să se calculeze produsul primelor n numere naturale. Se cer : - algoritmul; - pseudocodul; - schema logică.

68. APLICAŢII 1 . Se citesc două valori întregi a şi b. Se cere să se tipărească media lor aritmetică. 2. Se citesc 3 numere naturale. Se cere să se tipărească primul număr, suma dintre primul şi al doilea, suma celor trei numere. 3. Se citeşte x număr natural. Să se evalueze expresia de mai jos:

69. 4. Se citesc trei numere întregi. Să se tipărească (dacă există) numărul care este egal cu suma celorlalte două. 5. Se citeşte n (număr întreg). Se cere să se calculeze suma: S=1+3+5+…+n. 6. Să se calculeze suma: S=0,1+0,2+0,3+…+0,9. 7. Să se calculeze media aritmetică a primelor n numere naturale.

70. ITI MULTUMESC PENTRU RABDARE!!!