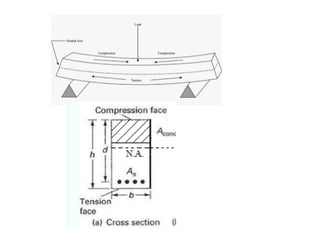
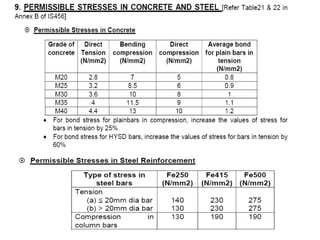
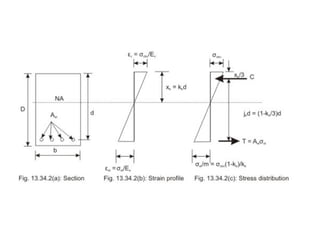
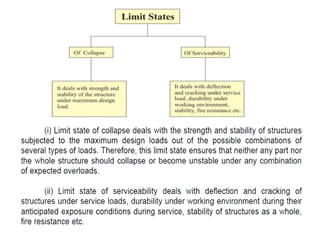
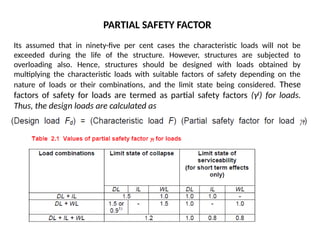
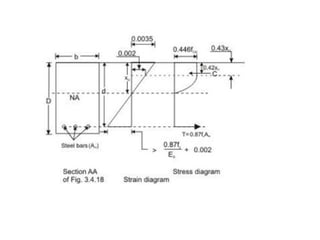
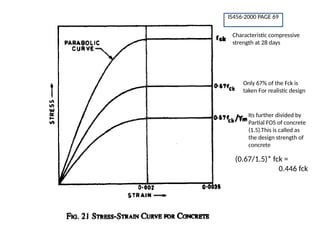
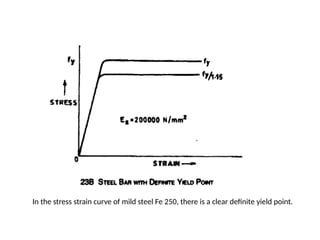
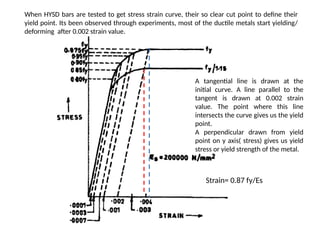
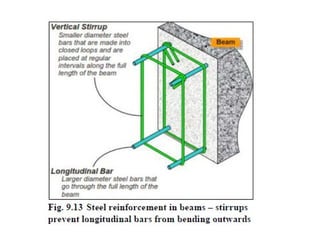
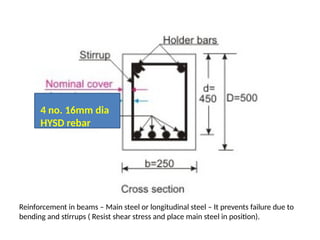
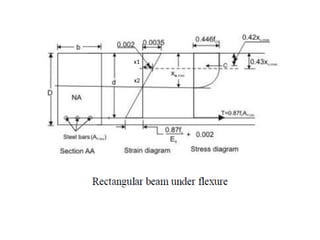
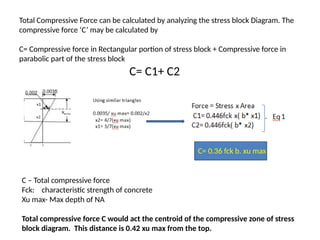
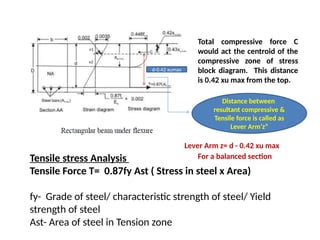
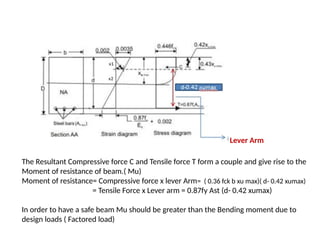
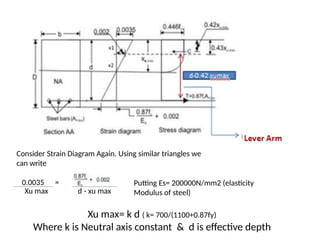
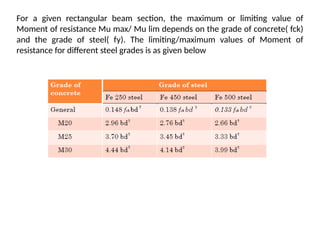
The document outlines the basics of reinforced concrete (RCC) design and the limit state method, emphasizing the distinction between functional and structural design. It details various design philosophies, including the working stress method, ultimate load method, and limit state method, focusing on key concepts such as characteristic strength and partial safety factors. It concludes with analysis principles for singly reinforced beams and explains design load combinations and characteristics necessary for safety and serviceability in structures.

1. Unit 3: RCC Basics and Limit state Method
Design

2. The design of any structure is categorized into the following two main
types :-
1) functional design
2) structural design.
FUNCTIONAL DESIGN
The structure to be constructed should be primarily serve the basic
purpose for which it is to be used and must have a pleasing look.
1. The building should provide happy environment inside as well as
outside.
2. Proper arrangements of rooms / halls to satisfy the need of the client
3. Good ventilation, lighting, acoustics,
4. Unobstructed view in the case of community halls, cinema halls, etc..
5. Sufficient head room, proper water supply and drainage arrangements.
6. Planting of trees , landscaping etc.
Keeping all these aspects in mind the architect/engineer has to decide
whether it should be a load bearing structure or R.C.C framed structure or
a steel structure etc..

3. The principle elements of a R.C building frame consists of :
1) slabs to cover large area
2) beams to support slabs and walls
3) columns to support beams
4) footings to distribute concentrated column loads over a large of the supporting
soil such that the bearing capacity of soil is not exceeded.
STRUCTURAL PLANNING
After getting an architectural plan of the buildings, the structural planning of the
building frame is done. This involves determination of the following :
a) positioning and orientation of column of columns
b) position of beams
c) spanning of slabs
d) layout of stairs
e) selecting proper type of footing

4. L5: Design Philosophies in RCC Design
A design philosophy is a set of assumptions and
procedures which are used to meet the conditions of
serviceability, safety, economy and functionality of the
structure. Several design philosophies have been
introduced from different parts of the world.

5. Introduction
A reinforced concrete structure should be designed to satisfy the
following criteria-
i) Adequate safety, in items stiffness and durability
ii) Reasonable economy.
The following design methods are used for the design of RCC
Structures.
a)The working stress method (WSM)/Allowable Stress
Design(ASD)
b) The ultimate load method (ULM)
c) The limit state method (LSM)

7. WORKING STRESS DESIGN/ ALLOWABLE STRESS METHOD
1. Old design philosophy.(This method was used in IS 456-1984 till revision IS 456:2000 was
introduced)
2. Based on empirical Approach
3. Based on linear elastic theory- where it is assumed that concrete is elastic and reinforcing
steel bars and concrete act together elastically.
4. The load-deflection relation is linear and both concrete and steel obey Hooke’s law.
5. This method ensured adequate safety by suitably restricting the stress in the materials (i.e.
concrete and steel) induced by the expected working loads on the structures. These specified
values of stresses which cant be exceeded are known as permissible stresses. The failure of
the structure will occur at a much higher load. The ratio of the failure loads to the working
loads is the factor of safety.
6. The method is designated as working stress method as the loads for the design of structures
are the service loads or the working loads.
7. The permissible stresses are determined dividing the characteristic strength fck
of the
material by the respective factor of safety.
8. The WSM uses a factor of safety of about 3 with respect to the cube strength of concrete and
a factor of safety of about 1.8 with respect to the yield strength of steel.
9. The FOS of steel is much lower than concrete due to high quality control during the
production of steel in the industry in comparison to preparing of concrete.
10. This method does not give an economical design due to use of high FOS. So its becoming
obsolete now .

9. 1. Plane sections before bending remain plane after bending.
2. Normally, concrete is not considered for taking the tensile stresses except otherwise
specifically permitted. Therefore, all tensile stresses are taken up by reinforcement
only.
3. The stress-strain relationship of steel and concrete is a straight line under working
loads.
4. The modular ratio m has the value of 280/3σcbc
, where σcbc
is the permissible
compressive stress in concrete due to bending in N/mm2
DEMERITS
1. Uneconomical design, bigger sections designed.
2. Factor of safety is on the stresses under working loads, uncertainty in terms of
loads cant be justified.
3. Effects like shrinkage and creep are difficult to consider in this method of design.

12. This is also known as load factor method or ultimate
strength method.
In this we make use of the nonlinear region of stress
strain curves of steel and concrete. The safety is
ensured by introducing load factor.
“Load factor is the ratio of ultimate strength to the
service loads”
The ULM makes it possible to consider the effects of
different loads acting simultaneously thus solving the
shortcomings of WSM. As the ultimate strength of the
material is considered we will get much slender sections
for columns and beams compared to WSM method. But
the serviceability criteria is not met because of large
deflections and cracks in the sections.
ULTIMATE LOAD METHOD

13. This philosophy is an advancement over the traditional design philosophies.
This is the globally used design method nowadays.
It considers the safety at the ultimate load and serviceability at the working load. Its an
extension of the WSM and ULM.
Limit states are the acceptable limits for the safety and serviceability requirements of the
structure before failure occurs.
The design of structures by this method will thus ensure that they will not reach limit
states and will not become unfit for the use for which they are intended.
Structures will not just fail or collapse by violating (exceeding) the limit states. Failure,
therefore, implies that clearly defined limit states of structural usefulness has been
exceeded.
LIMIT STAE METHOD OF DESIGN

15. Important Terminology
Characteristic strength of materials.
The term ‘characteristic strength‘ means that value of the strength of material below
which not more than minimum acceptable percentage of test results are expected
to fall. IS 456:2000 have accepted the minimum acceptable percentage as 5% for
reinforced concrete structures. This means that there is 5% for probability or
chance of the actual strength being less than the characteristic strength.
Characteristic strength of concrete
Characteristic strength of concrete is denoted by fck (N/mm2) and its value is
different for different grades of concrete e.g. M 15, M25 etc. In the symbol ‘M‘ used
for designation of concrete mix, refers to the mix and the number refers to the
specified characteristic compressive strength of 150 mm size cube at 28 days
expressed in N/mm2
Characteristic strength of steel
Until the relevant Indian Standard specification for reinforcing steel are modified to
include the concept of characteristic strength, the characteristic value shall be
assumed as the minimum yield stress or 0.2% proof stress specified in the relevant
Indian Standard specification. The characteristic strength of steel designated by
symbol fy (N/mm2)
Characteristic loads
The term ‘Characteristic load‘ means that values of load which has a 95% probability of
not being exceeded during that life of the structure.

16. PARTIAL SAFETY FACTOR
Its assumed that in ninety-five per cent cases the characteristic loads will not be
exceeded during the life of the structure. However, structures are subjected to
overloading also. Hence, structures should be designed with loads obtained by
multiplying the characteristic loads with suitable factors of safety depending on the
nature of loads or their combinations, and the limit state being considered. These
factors of safety for loads are termed as partial safety factors (γf
) for loads.
Thus, the design loads are calculated as

17. Clause 36.4.2 of IS 456 states that for concrete and steel
should be taken as 1.5 and 1.15, respectively when assessing the
strength of the structures or structural members employing limit
state of collapse.
It is worth mentioning that partial safety factor for steel (1.15) is
comparatively lower than that of concrete (1.5) because the steel
for reinforcement is produced in steel plants and commercially
available in specific diameters with expected better quality control
than that of concrete

18. Types of Loads on a structure-
1. Dead Load
2. Live Load
3. Wind load
4. Earthquake load
5. Snow load
6. Other loads- impact, blast etc
Vertical loads/gravity loads
Horizontal/lateral loads
Dead load of a structure mainly includes the self weight of building. Which
comprises of structural members, walls, fixtures , finishes etc. It remains
mostly the same throughout the life of a structure. IS875 PART 1 provides
the densities of various construction materials. That is useful in DL
calculation.
Live load/imposed loads are the loads which keep on changing. It depends
on the type of building, purpose, occupancy etc. This includes
people ,movable furniture etc IS875-PART2 gives the live load values to be
taken for different buildings.

19. LIMIT STATE METHOD OF DESIGN (IS 456-2000)
1. This method deals with failure of
structure due to shear forces, Bending
moment, Torsion, Axial force or their
combination.
2. Structure design- Codal provision ( IS
456-2000) recommends use of load
combinations for safe design (The worst
load combination is adopted in design)
• 1.5DL+ 1.5 LL/IL
• 1.2(DL+LL+ WL/EQ)
• 1.5DL+ 1.5 WL/EQ
• 0.9DL + 1.5 WL/EQ
Which ever combination
gives the max value of
load would be taken in
design. This method
ensures safety of
structure against collapse
1. This method deals with
deflection, Cracking,
Corrosion, Abrasion , Fire
resistance of structure.
2. Following load
combinations used in this
method
• 1.0DL+1.0LL
• 1.0DL+1.0WL/EQ
• DL+0.8( LL+WL/EQ)
Talks about strength criteria &
ensures safety of structure
Enhances service life /durability of
structure
Possibility Of heavy EQ and heavy wind is a very rare possibility. Hence either EQ or WL

20. Important terms
Fck – Characteristic compressive strength of concrete/ Grade of concrete
Example
1. M20. Fck= 20 N/mm2
2. M35 Fck= 35 N/mm2
Fy- Characteristic strength of steel/ Yield strength/ Grade of steel
Example
3. Fe250, fy= 250N/mm2
4. Fe415 fy= 415N/mm2
5. Fe500 fy= 500 N/mm2
Design Strength = Characteristic strength/ factor of safety
Factor Of safety (FOS) for concrete= 1.5
Factor of safety (FOS) for steel= 1.15
Lesser value of FOS for steel in comparison to concrete is due to high quality
control adopted in its production in workshops/ steel mills.
Recommended by IS456-2000

21. Characteristic Load
Its that load which has 95% chances of not being exceeded in the entire life span of
structure
Design Load- Characteristic Load x factor of safety
As per IS 456-2000, FOS for load is 1.5.

22. Limit state method- Basic Assumptions (IS 456- 2000)
a) Plane sections normal to the beam axis remain plane after bending. Strain variation in the
beam is linear
b) The maximum compressive strain in concrete (at the outermost fibre) shall be taken as 0.0035 in
bending. This curve is parabolic upto a strain value of 0.002 and After that it’s a straight line till
strain value 0.0035. The max strain Value of 0.0035 is taken as its been observed concrete cracks
after exceeding this strain value. (based on experiments) Hence we restrict our analysis upto this
strain value of 0.0035
c) Stress block is parabolic from Neutral axis to strain 0.002 and rectangular upto the strain value of
0.0035
d) Tensile strength of concrete is ignored. As the entire tensile stress would be taken up by steel
reinforcement
e) The max strain in tensile steel shall not be less than

24. Only 67% of the Fck is
taken For realistic design
Its further divided by
Partial FOS of concrete
(1.5).This is called as
the design strength of
concrete
Characteristic compressive
strength at 28 days
IS456-2000 PAGE 69
456
(0.67/1.5)* fck =
0.446 fck

25. In the stress strain curve of mild steel Fe 250, there is a clear definite yield point.

26. When HYSD bars are tested to get stress strain curve, their so clear cut point to define their
yield point. Its been observed through experiments, most of the ductile metals start yielding/
deforming after 0.002 strain value.
A tangential line is drawn at the
initial curve. A line parallel to the
tangent is drawn at 0.002 strain
value. The point where this line
intersects the curve gives us the yield
point.
A perpendicular drawn from yield
point on y axis( stress) gives us yield
stress or yield strength of the metal.
Strain= 0.87 fy/Es

27. ANALYSIS OF SINGLY
REINFORCED BEAM UNDER
UNIFORMLY DISTRIBUTED
LOAD (UDL)

28. Singly reinforced beams are those beams which are reinforced in tension
zone only. As in case of simply supported beam, tension zone develops
below the Neutral axis, hence rebars/ steel reinforcement is provided at the
bottom of the beam.
However 2 anchor bars/ hanger bars are always provided, which help in
holding the stirrups. The se anchor bars are useful in following ways-
1. They hold the main reinforcement in place
2. Also act as shear reinforcement.
b- width of the beam section
d – Effective depth of beam
D- Overall depth of the beam
Effective depth of the beam is defined as the
depth from the top face of the beam section
to the center of the steel reinforcement.
Distance from the center of the main steel
bar to the bottom face of the beam is called
effective cover
Distance from the outer surface of the main steel bar to the bottom face of the beam
is called clear cover or Nominal cover

30. 4 no. 16mm dia
HYSD rebar
Reinforcement in beams – Main steel or longitudinal steel – It prevents failure due to
bending and stirrups ( Resist shear stress and place main steel in position).

31. Effective cover= Clear cover + Diameter of rebar/2
Overall depth= Effective depth + effective cover
1. For a singly reinforced beams with cross section details 300x450mm , clear cover
15mm, diameter of bars used 16mm. If effective depth is 450mm mm. Calculate the
over all depth. Draw a sketch
2. Calculate effective depth for a SRB, with width 300mm and over all depth 500mm.
Assume a clear cover of 25 mm and the diameter of HYSD bars is 16mm. Make a
neat sketch
Why Do we provide cover to the reinforcement?

32. x1
x2

33. Total Compressive Force can be calculated by analyzing the stress block Diagram. The
compressive force ‘C’ may be calculated by
C= Compressive force in Rectangular portion of stress block + Compressive force in
parabolic part of the stress block
C= C1+ C2
C= 0.36 fck b. xu max
C – Total compressive force
Fck: characteristic strength of concrete
Xu max- Max depth of NA
Total compressive force C would act the centroid of the compressive zone of stress
block diagram. This distance is 0.42 xu max from the top.

34. Total compressive force C
would act the centroid of the
compressive zone of stress
block diagram. This distance
is 0.42 xu max from the top.
Tensile stress Analysis
Tensile Force T= 0.87fy Ast ( Stress in steel x Area)
fy- Grade of steel/ characteristic strength of steel/ Yield
strength of steel
Ast- Area of steel in Tension zone
d-0.42 xumax
Distance between
resultant compressive &
Tensile force is called as
Lever Arm’z”
Lever Arm z= d - 0.42 xu max
For a balanced section

35. Lever Arm
The Resultant Compressive force C and Tensile force T form a couple and give rise to the
Moment of resistance of beam.( Mu)
Moment of resistance= Compressive force x lever Arm= ( 0.36 fck b xu max)( d- 0.42 xumax)
= Tensile Force x Lever arm = 0.87fy Ast (d- 0.42 xumax)
In order to have a safe beam Mu should be greater than the Bending moment due to
design loads ( Factored load)

36. Consider Strain Diagram Again. Using similar triangles we
can write
0.0035 =
Xu max d - xu max
Putting Es= 200000N/mm2 (elasticity
Modulus of steel)
Xu max= k d ( k= 700/(1100+0.87fy)
Where k is Neutral axis constant & d is effective depth

37. Therefore Maximum/ Limiting Depth of neutral axis depends on the grade of
the steel used
Fe250= 0.53d
Fe415= 0.48d
Fe500= 0.46d

38. Types Of Beam Sections
Max failure strain value in concrete= 0.0035
Max failure strain value in steel= 0.002+ 0.87fy/Es
A balanced steel section is such a section in which steel and concrete reach their failure
strains simultaneously.
Therefore xu= xumax
Xu= depth of NA
Xumax= max depth/limiting
depth of NA

39. Under reinforced beam section means that the steel would reach its max strain
value before the concrete. In this case Depth of NA would be less than the
maximum depth of NA . Therefore xu < xu max.
1. Amount of steel in these sections is less than that of a balanced section.
2. In this type of section, the failure type is Ductile in nature.
3. Ductile failure means the one which gives us sufficient warning before
collapse.
4. Hence these sections don’t fail abruptly as steel starts yielding before
concrete.
5. A beam should be preferably designed as a Under reinforced section

40. In an Over reinforced section, the concrete reaches its failure strain prior to steel. Hence
the depth of NA is greater than the Max depth of neutral axis.
1. xu> xu max
2. In these sections steel provided is greater than that in a balanced section
3. This section fails in an abrupt manner without any warning.
4. As the concrete is a brittle material, it collapses suddenly once it reaches its failure
strain value of 0.0035
5. Over reinforced sections are banned as per IS 456-2000

41. Compressive force C= 0.36 fck b xu
Tensile force T= 0.87fy Ast
For equilibrium C= T
0.36fck b xu= 0.87fy Ast
Xu = Actual depth of Neutral axis

42. Q1: Consider a Simply supported singly reinforced beam section as
shown Check if the section is balanced, U/R or O/R Provided with 4 No.s ,
12mm diameter Fe415 steel bars,M25 grade concerte 200mm
300mm
Solution: Assuming 300mm to be the effective depth
d= 300mm
b= 200mm
Area of steel (Ast)
( cross section area of 12mm diameter bar) x No.
π /4( 12*12)*4= 452 sqmm
Step 1: Calculate max depth of NA, xu max
Max depth of NA depends on grade of steel. Here its
Fe415, fy=415 N/mm2
so xu max= 0.48d= 0.48x 300= 144mm
Step 2: Actual depth of NA Xu= 90.66mm
Step 3: Compare xu & xu max Here xu< xu max. So its an Under reinforced section.

43. Q3: Calculate lever arm(z) for the given beam section with
M25 concrete, 3, no. 16mm φ Fe 415 steel.
250mm
360mm
40mm
Solution: Lever Arm z= d-0.42xu

44. Xu max
Xu max

45. For a given rectangular beam section, the maximum or limiting value of
Moment of resistance Mu max/ Mu lim depends on the grade of concrete( fck)
and the grade of steel( fy). The limiting/maximum values of Moment of
resistance for different steel grades is as given below

46. Under Reinforced section

47. Balanced Section

49. 0.36 fck b xu
0.36x20x 250x Xu
1800 Xu
Area of steel Ast
0.87 fy Ast
On equating C= T, Xu= 68mm
Problem No. 1

50. Calculate Xumax.
For Fe415 grade, xumax= 0.48d= 0.48x 310= 148.8mm
Xu max > Xu. Hence its an Under reinforced section.
0.87 fy Ast (d- 0.42 Xu)
d-0.42Xu

51. The same problem could be solved by using formula of Mu for case 1 , Under
reinforced section.
0.87 x 415 x 3x 113 x310 1 - (415x3x 113)
(20 x 250 x 310)
37942744.5( 1- 140685 )
1550000
=34 527 897.04 N-mm
=34.53 KN-m

52. Problem No. 2
Calculate Moment of resistance of rectangular beam section
given in Problem 1 with Grade of concrete M20 and Grade of
steel Fe500.
( Answer Xu= 82mm and Mu= 40.65KNm)
Problem No. 3

54. To find Area of steel - A st ?????