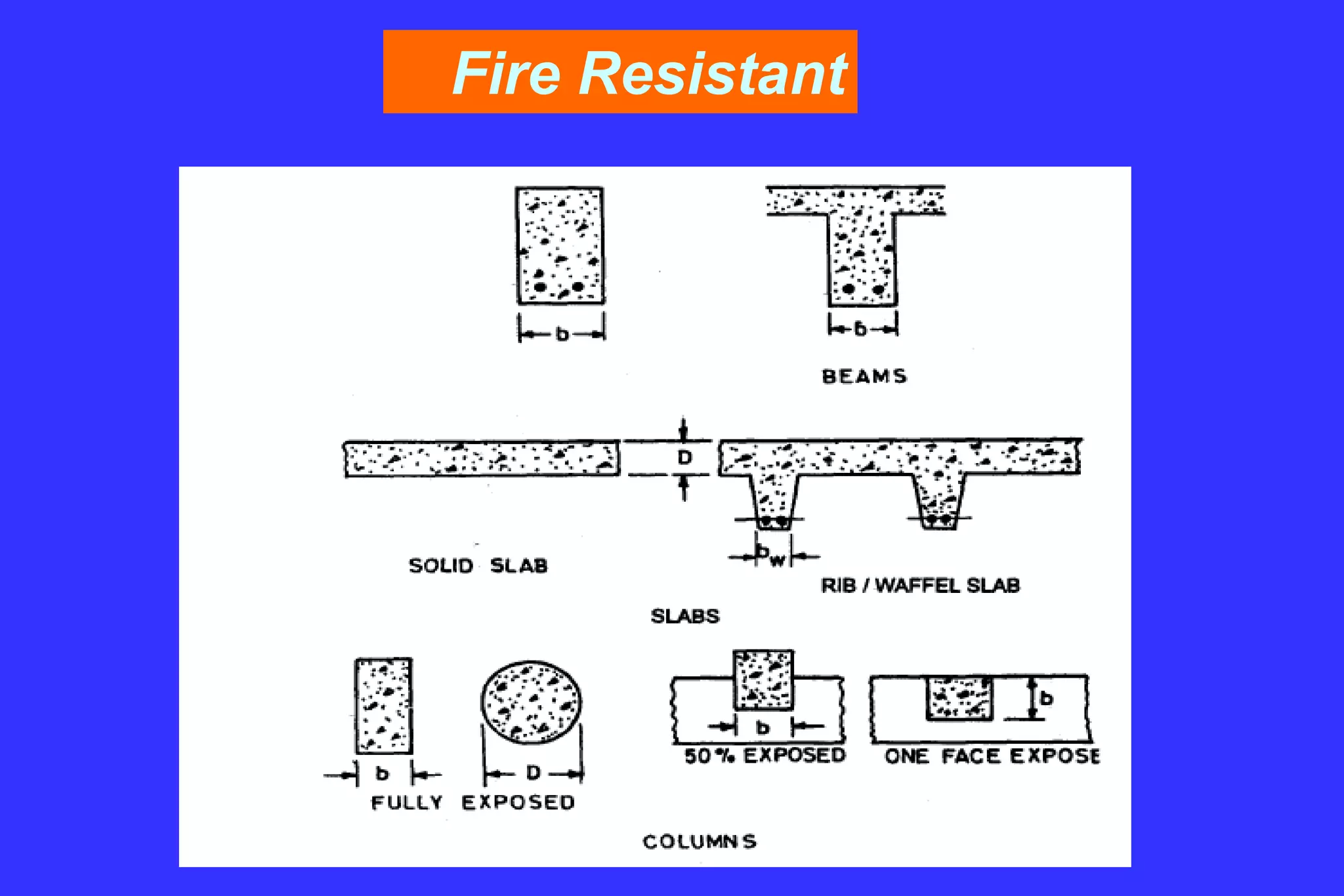
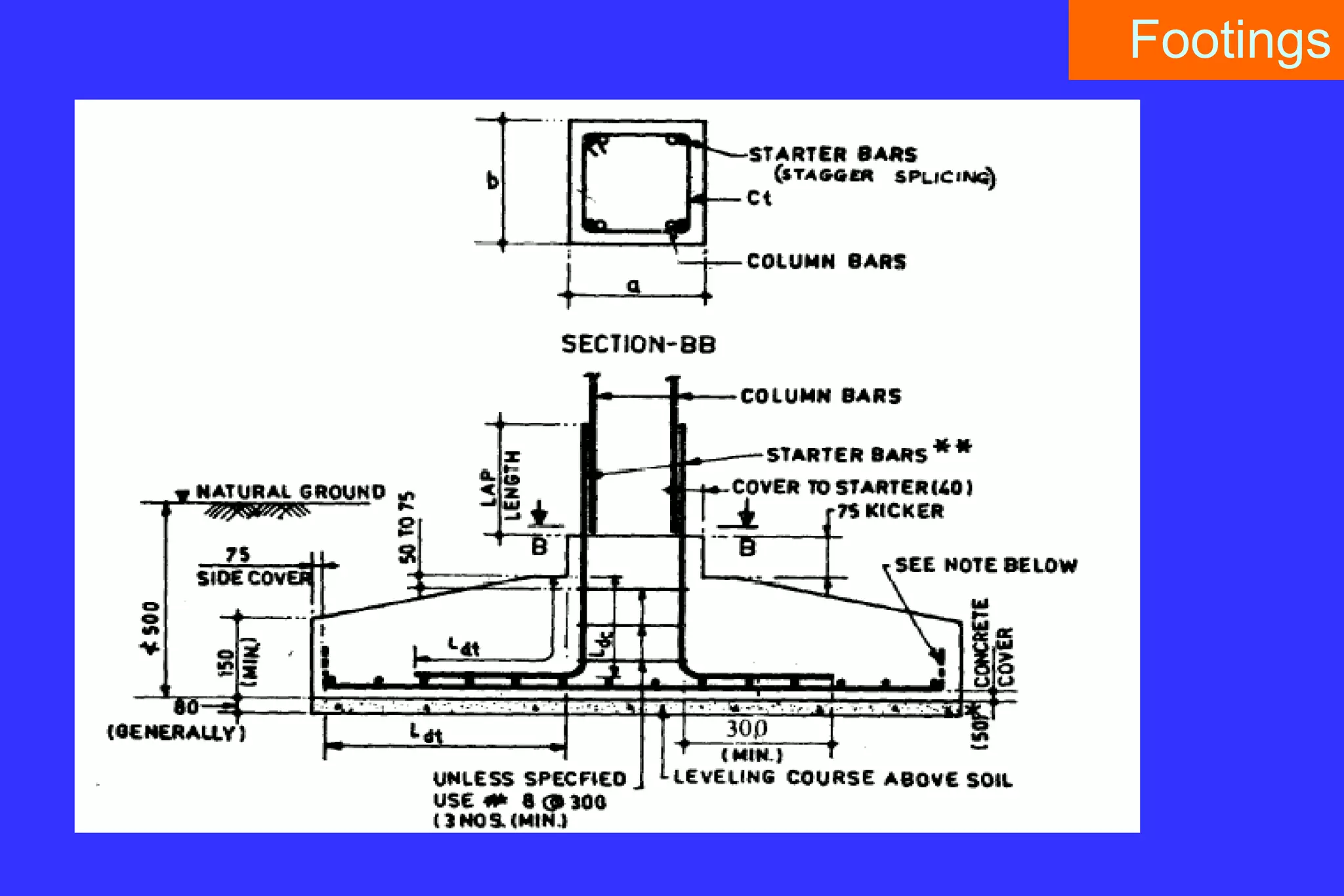
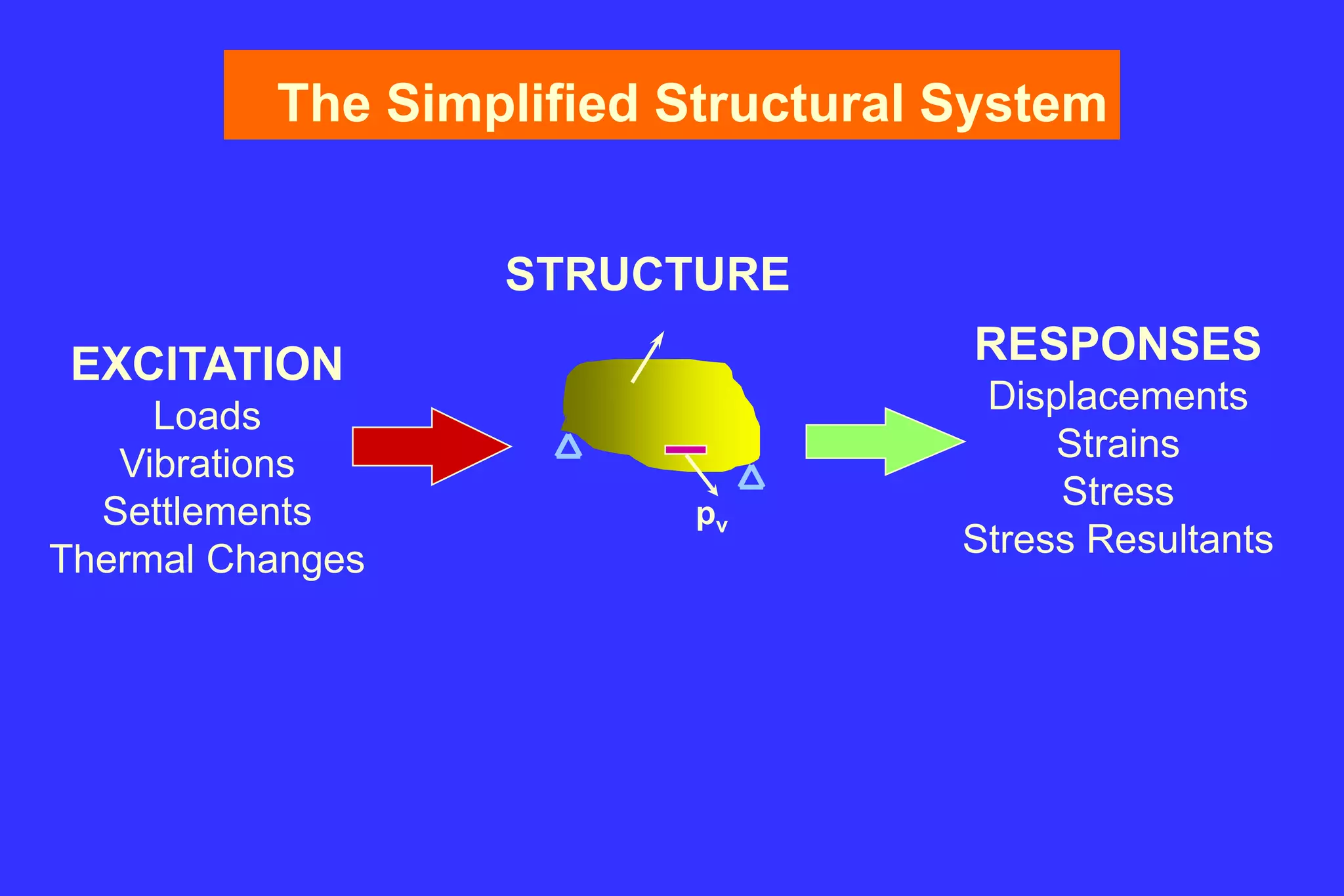
This document provides an overview of structural design concepts and processes. It discusses: 1. The overall design process including conception, modeling, analysis, design, detailing, drafting and costing. 2. Key structural elements like beams, columns, slabs, shear walls, footings and their design. 3. Concepts of the gravity load resisting system, lateral load resisting system and floor diaphragm. 4. Methods of structural analysis including modeling approaches and consideration of loads and load combinations. 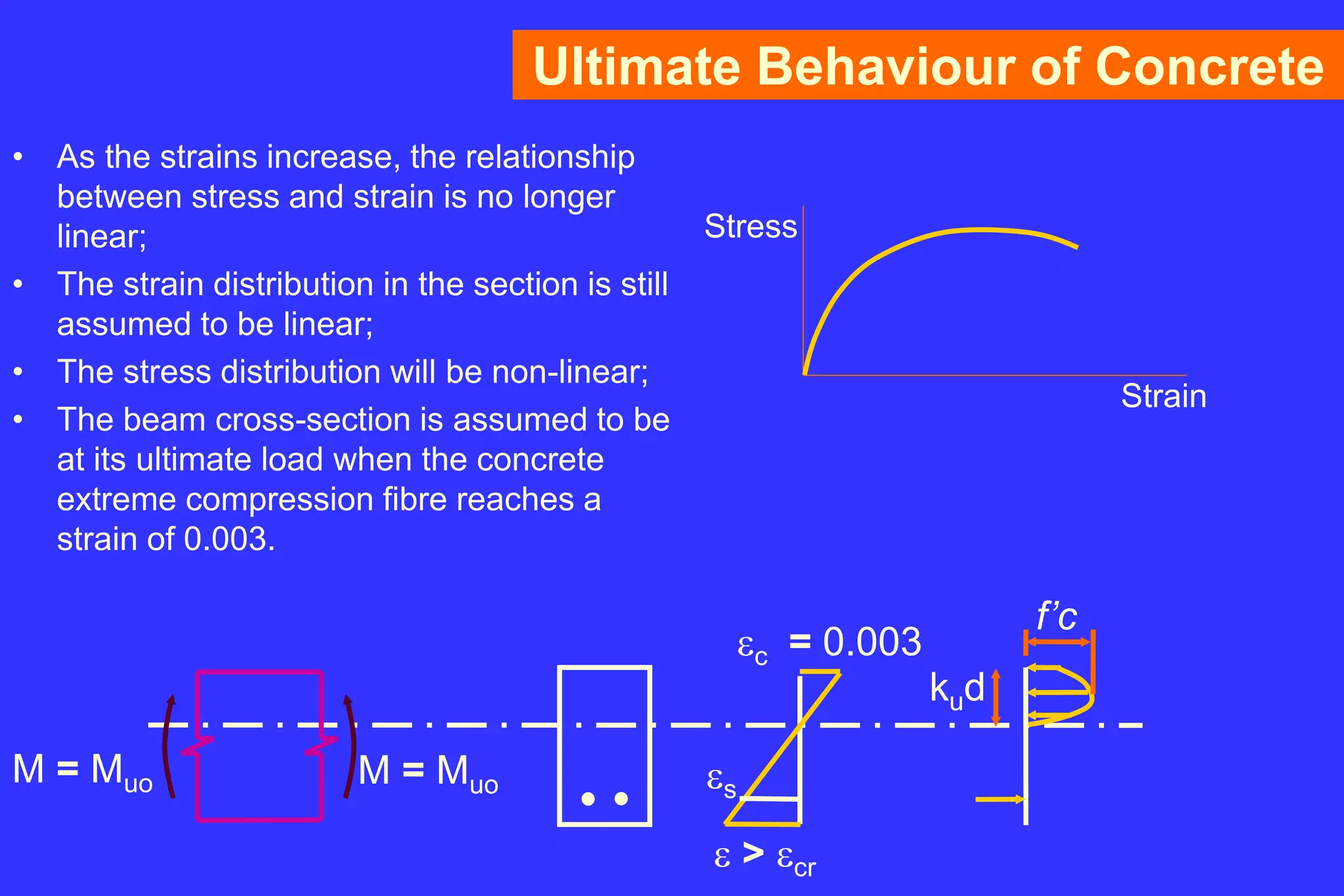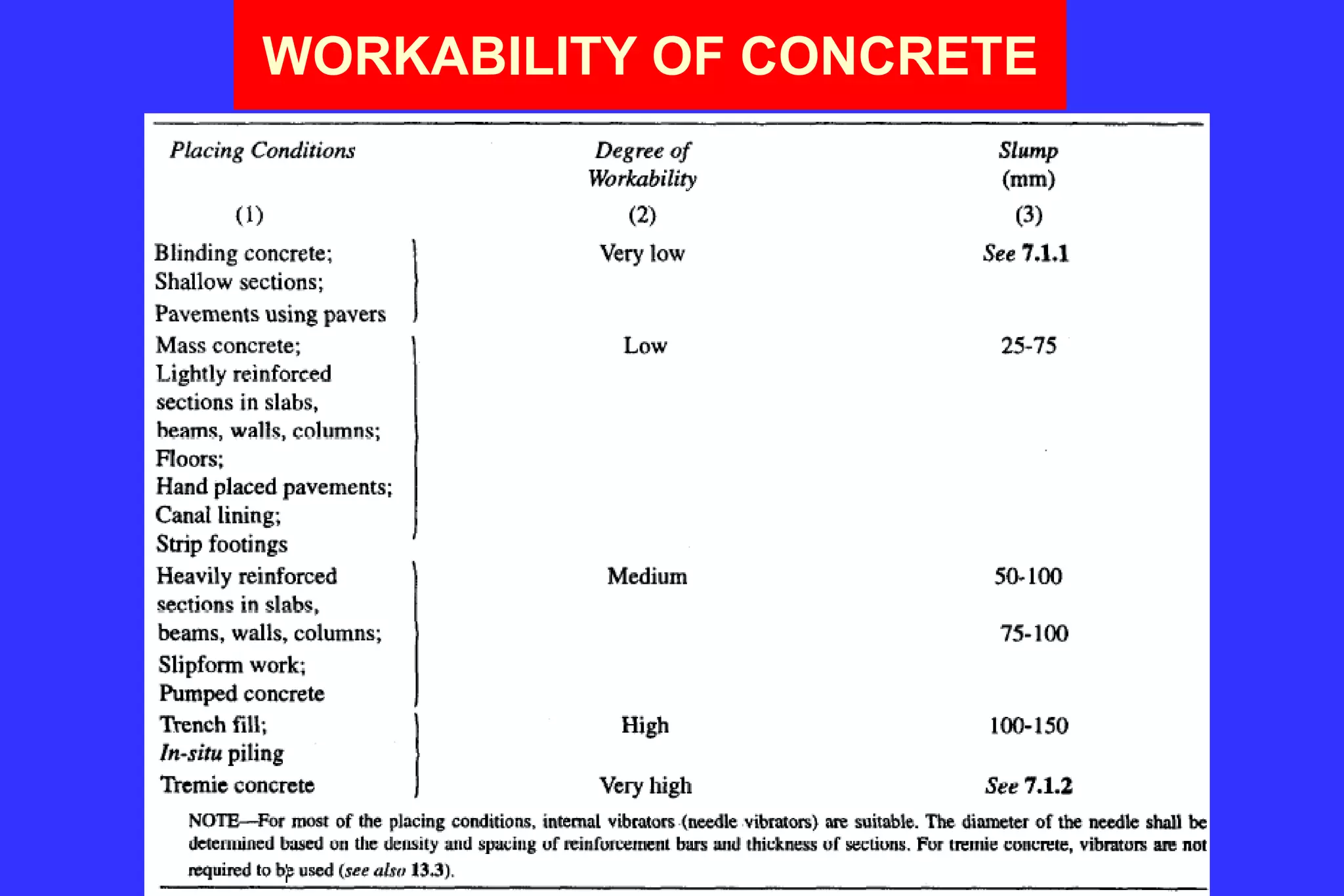5. Design principles for concrete including properties, reinforcement, durability and mix proportioning.

1. AQUIB ANSARI
(Assistant Professor)
Department of Civil Engineering
A.C.E.T Nagpur

2. Overall Design Process
• Conception
• Modeling
• Analysis
• Design
• Detailing
• Drafting
• Costing

3. Beams, Columns, Two-way Slabs, Flat Slabs, Pile caps
Shear Walls, Deep Beams, Isolated Footings, Combined Footings
Sub-structure and Member Design
Frame and Shear Walls
Lateral Load Resisting System Floor Slab System
Gravity Load Resisting System
Building Structure
Floor Diaphragm
The Building Structural System - Physical

4. The Building Structural System - Conceptual
• The Gravity Load Resisting System
– The structural system (beams, slab, girders,
columns, etc) that act primarily to support the gravity
or vertical loads
• The Lateral Load Resisting System
– The structural system (columns, shear walls, bracing,
etc) that primarily acts to resist the lateral loads
• The Floor Diaphragm
– The structural system that transfers lateral loads to
the lateral load resisting system and provides in-
plane floor stiffness

5. Building Response
Objective: To determine the load path gravity and lateral loads
• For Gravity Loads - How Gravity Loads are Distributed
– Analysis of Gravity Load Resisting System for:
• Dead Load, Live Live Load, Pattern Loads, temperature,
shrinkage
– Important Elements: Floor slabs, beams, openings, Joists, etc.
• For Lateral Loads – How Lateral Loads are Distributed
– Analysis of Lateral Load Resisting System for:
• Wind Loads, Seismic Loads, Structural Un-symmetry
– Important elements: Columns, shear walls, bracing , beams

6. The Simplified Structural System
STRUCTURE
pv
EXCITATION
Loads
Vibrations
Settlements
Thermal Changes
RESPONSES
Displacements
Strains
Stress
Stress Resultants

7. Global Modeling of Structural Geometry
(b) Solid Model (c) 3D Plate-Frame (d) 3D Frame
(a) Real Structure
(e) 2D Frame
Fig. 1 Various Ways to Model a Real Struture
(f) Grid-Plate

8. Structure Types
• Cable Structures
• Cable Nets
• Cable Stayed
• Bar Structures
• 2D/3D Trusses
• 2D/3D Frames, Grids
• Surface Structures
• Plate, Shell
• In-Plane, Plane Stress
• Solid Structures

9. Introduction to Structural Design
“Concrete”

10. Concrete Properties
Strain
Stress
Typical stress-strain curve for a concrete cylinder in compression

11. Concrete Properties
• Concrete stress-strain curve shows no definite
yield point;
• Concrete does not have the large plastic
deformation capacity of structural steel in the
stress-strain curve, and so does not display the
same ductile behaviour;
• Concrete has a brittle failure.

12. Pre-cracking Behaviour of Concrete
e < ecr
e < ecr
M < Mcr M < Mcr
f < fcf
Strain
Stress
At relatively low strains, the
stress-strain relationship is
approximately linear
fcf is the actual flexural
tensile strength where f’cf is
the characteristic flexural
tensile strength.

13. Ultimate Behaviour of Concrete
• As the strains increase, the relationship
between stress and strain is no longer
linear;
• The strain distribution in the section is still
assumed to be linear;
• The stress distribution will be non-linear;
• The beam cross-section is assumed to be
at its ultimate load when the concrete
extreme compression fibre reaches a
strain of 0.003.
Strain
Stress
ec = 0.003
e > ecr
M = Muo M = Muo es
f’c
kud

14. Types of Concrete Section
• The calculation procedure varies depending on when
the steel yields;
• In under-reinforced sections the steel has already
yielded when the concrete reaches its ultimate state
with strains of 0.003 at the extreme compressive
fibre;
• In balanced sections the steel yields just as the
concrete reaches its ultimate state with strains of
0.003 at the extreme compressive fibre;
• In over-reinforced sections the steel has not
yielded when the concrete reaches its ultimate state
with strains of 0.003 at the extreme compressive
fibre;

15. Review of IS 456:2000

16. Reinforcement
• Mild steel and medium tensile steel bars conforming to IS
432 (Part 1).
• High strength deformed steel bars conforming to IS 1786.
• Hard-drawn steel wire fabric conforming to IS 1566.
• Structural steel conforming to Grade A of IS 2062
Fe 250
Fe 415
Fe 500
Fe 550

17. Concrete

18. Concrete
• For concrete of grade greater than M55, design
parameters given in the standards may not be
applicable and the values may be obtained from
specialized literatures and experimental results.
• Comments: Whether RCC concrete is to be taken as
ordinary concrete or Standard concrete?. If it is to be
considered as standard Concrete, then minimum grade
of concrete will be M25.
• For water retaining structures, it must be grade M30
minimum.

19. Modulus of Elasticity
• Ec = 5000 fck in N/mm2
• Actual measured values may differ by 20% from the
values obtained from the expression.
• Comments: E value does not affect the static analysis
for vertical and horizontal forces, except the secondary
forces. However, change in E value significantly affects
the detailed dynamic analysis. The fundamental time
period for SDOF system may vary from 10-12%.

20. Tensile Strength of Concrete

21. Tensile Strength of Concrete

22. Tensile Strength of Concrete

23. Shrinkage
The total shrinkage of concrete depends upon the
constituents of concrete, size of the member and
environmental conditions. For a given humidity and
temperature, the total shrinkage of concrete is most
influenced by the total amount of water present in the
concrete at the time of mixing and, to a lesser extent, by
the cement content .
In the absence of test data, the approximate
value of the total shrinkage strain for design may
be taken as 0.000 3

24. Thermal Expansion
The coefficient of thermal expansion depends on nature
of cement, the aggregate, the cement content, the
relative humidity and the size of sections-The value
of coefficient of thermal expansion for concrete with
different aggregates may be taken as below:

25. WORKABILITY OF CONCRETE

26. DURABILITY OF CONCRETE
• the environment;
• the cover to embedded steel;
• the type and quality of constituent materials;
• the cement content and water/cement ratio of
• the concrete;
• workmanship, to obtain full compaction and
• efficient curing; and
• the shape and size of the member.

27. Exposure Conditions: General environment

28. Maximum cement content

29. CONCRETE MIX PROPORTIONING:
Information Required

30. FORM WORK : Stripping Time

31. INSPECTION AND TESTING OF STRUCTURES
Core Test
Concrete in the member represented by a core test shall
be considered acceptable if the average equivalent cube
strength of the cores is equal to at least 85 percent of the
cube strength of the grade of concrete specified for the
corresponding age and no individual core has a strength
less than 75 percent.

32. INSPECTION AND TESTING OF STRUCTURES
Load Tests for Flexural Members
The structure should be subjected to a load equal to full
dead load of the structure plus 1.25 times the imposed
load for a period of 24 h and then the imposed load shall
be removed.
The deflection due to imposed load only shall be recorded.
If within 24 h of removal of the imposed load, the structure
does not recover at least 75 percent of the deflection under
superimposed load, the test may be repeated after a lapse
of 72 h. If the recovery is less than 80 percent, the
structure shall be deemed to be unacceptable.

33. INSPECTION AND TESTING OF STRUCTURES
Load Tests for Flexural Members
The structure should be subjected to a load equal to full
dead load of the structure plus 1.25 times the imposed
load for a period of 24 h and then the imposed load shall
be removed.
The deflection due to imposed load only shall be recorded.
If within 24 h of removal of the imposed load, the structure
does not recover at least 75 percent of the deflection under
superimposed load, the test may be repeated after a lapse
of 72 h. If the recovery is less than 80 percent, the
structure shall be deemed to be unacceptable.

34. INSPECTION AND TESTING OF STRUCTURES
non-destructive Tests
Non-destructive tests are used to obtain estimation of the
properties of concrete in the structure. The methods
adopted include ultrasonic pulse velocity and rebound
hammer .
Non destructive tests provide alternatives to core tests for
estimating the strength of concrete in a structure, or can
supplement the data obtained from a limited number of
cores.

35. Methods of Design
Structure and structural elements shall normally be
designed by Limit State Method.
Where the Limit State Method can not be conveniently
adopted, Working Stress Method.
Designs based on experimental investigations on
models or full size structure or element may be
accepted

36. Loads
• Dead Loads
• Imposed Loads
• Wind Loads
• Snow Loads
• Earthquake Forces
• Shrinkage, Creep and Temperature
Effects
• Other Forces and Effects
1. Foundation movement,
2. Elastic axial shortening,
3. Soil and fluid pressures,
4. Vibration, Fatigue, Impact,
5. Erection loads
6. Stress concentration effect due to point load and the like.

37. Load Combinations
1. 1.5 DL + 1. 5 LL
2. 1.2 DL + 1.2 LL  1.2 EQ / WL
3. 1.5 DL  1.5 EQ / WL
4. 0.9 DL  1.5 EQ / WL

38. Load Combinations as per IS:875-1987
(P-V)
i. DL
ii. DL + IL
iii. DL + WL/EQ
iv. DL + IL + WL/EQ
v. DL + WL/EQ + TL
vi. DL + IL + WL/EQ + TL
Note: Load with only Wind loads are considered.

39. Load Combinations as per IS:456-2000
(Limit State of Collapse)
i. 1.5 DL + 1.5 IL
ii. 1.5 DL + 1.5 EQX ( Earthquake towards left)
iii. 1.5 DL – 1.5 EQX (Earthquake towards right)
iv. 1.2 DL + 1.2 IL + 1.2 EQX
v. 1.2 DL + 1.2 IL - 1.2 EQX
vi. 0.9 DL + 1.5 EQX
vii. 0.9 DL + 1.5 EQX
Note: Load with only eqx load is considered.

40. STABILITY OF THE STRUCTURE – Overturning
• The stability of a structure as a whole against
overturning shall be ensured so that the restoring
moment shall be not less than the sum of 1.2 times
the maximum overturning moment due to the
characteristic dead load and 1.4 times the
maximum overturning moment due to the
characteristic imposed loads.
• In cases where dead load provides the restoring
moment, only 0.9 times the characteristic dead load
shall be considered. Restoring moment due to
imposed loads shall be ignored.

41. STABILITY OF THE STRUCTURE - Sliding
• The structure shall have a factor against sliding of
not less than 1.4 under the most adverse
combination of the applied characteristic forces. In
this case only 0.9 times the characteristic dead load
shall be taken into account.

42. FIRE RESISTANCE

43. FIRE RESISTANCE

44. Analysis
• All the structures may be analyzed by the linear elastic
theory to calculate internal actions produced by design.
In lieu of rigorous elastic analysis, a simplified analysis
as given in 22.4 for frames and as given in 22.5 for
continuous beams may be adopted.
• Where side sway consideration becomes critical due to
unsymmetry in geometry or loading, rigorous analysis
may be required.

45. Effective Span

46. Effective Span
• Continuous Beam or Slab - In the case of continuous beam or slab,
if the width of the support is less than l/12 of the clear span, the
effective span shall be as in SS Beam. If the supports are wider
than I/12 of the clear span or 600 mm whichever is less, the
effective span shall be taken as under:
• 1) For end span with one end fixed and the other continuous or for
intermediate spans, the effective span shall Abe the clear span
between supports;
• 2) For end span with one end free and the other continuous, the
effective span shall be equal to the clear span plus half the
effective depth of the beam or slab or the clear span plus half the
width of the discontinuous support, whichever is less;3) In the
case of spans with roller or rocker bearings, the effective span
shall always be the distance between the centres of bearings.

47. Effective Span
• Frames-In the analysis of a continuous frame,centre to
centre distance shall be used.

48. Critical Sections for Moment
• For monolithic construction, the moments computed at
the face of the supports shall be used in the design of
the members at those sections.

49. Effective span for cantilever

50. Stiffness
• The relative stiffness of the members may be based on
the moment of inertia of the section determined on the
basis of any one of the following definitions:.
• Gross section - The cross-section of The member
ignoring reinforcement;
• Transformed section - The concrete cross section plus
the area of reinforcement transformed on the basis of
modular ratio ; or
• Cracked section - The area of concrete in compression
plus the area of reinforcement transformed on the basis
of modular ratio.
The assumptions made shall be consistent for all the members
of the structure throughout any analysis..

51. Arrangement of Imposed Load
Consideration may be limited to combinations Of:
• Design dead load on all spans with full design imposed
load on two adjacent spans; and
Design dead load on all spans with full design imposed
load on alternate spans.
• When design imposed load does not exceed three-
fourths of the design dead load, the load arrangement
may be design dead load and design imposed load on
all the spans.

52. Critical Section for Shear
The shears computed at the face of the
support shall be used in the design of the
member at that section except :
When the reaction in the direction of the applied shear
introduces compression into the end region of the
member, sections located at a distance less than d from
the face of the support may be designed for the same
shear as that computed at distance d

53. Critical Section for Shear

54. Control of Deflection
• The final deflection due to all loads including the effects of
temperature, creep and shrinkage and measured from the
as-cast level of the , supports of floors, roofs and all other
horizontal members, should not normally exceed span/250.
• The deflection including the effects of temperature, creep
and shrinkage occurring after erection of partitions and the
application of finishes should not normally exceed span/350
or 20 mm whichever is less
For deflection calculations, appropriate values
of moment of inertia as specified in Annex C should
be used.

55. Control of Deflection
• The vertical deflection limits may be generally be
assumed to be satisfied provided that the span to
effective depth ratios (for beams and slabs) are not
greater the values obtained as below:
• Cantilever - 7
• Simply supported - 20
• Continuous - 26
• The values may be modified as per the area and the
stress of steel for tension reinforcement.
The figures gives higher multiplying factor for lower
stresses and vice versa.

56. Two Way Slabs
• For two way slabs, of shorter span less than or equal to
3.5m, the span to overall depth ratios given below may
generally be assumed to satisfy vertical deflection limits
for loadings class upto 3 kN/sqm
Fe250 Fe415
Simply supported slabs 35 28
Continuous slabs 40 32

57. 0
.
2
log
625
.
0
00322
.
0
225
.
0
1
1
10










pt
fs
F

58. 5
.
1
3
1
2 









pc
pc
F
8
.
0
3
.
0
7
2
8
.
0
3 









bf
bw
F

59. Slenderness Limits for Beams
A simply supported or continuous beam shall be so
proportioned that the clear distance between the lateral
restraints does not exceed 60 b or 250 b2 /d whichever
is less, where where d is the effective depth of the
beam and b the breadth of the compression face
midway between the lateral restraints.
For a cantilever, the clear distance from the free end of
the cantilever to the lateral restraint shall not exceed 25 b
or 100 b2 /d whichever is less.

60. Slabs Continuous Over Supports

61. Slabs Monolithic with Supports
Bending moments in slabs (except flat slabs)constructed
monolithically with the supports shall be calculated by
taking such slabs either as continuous over supports and
capable of free rotation, or as members of a continuous
framework with the supports, taking into account the
stiffness of such supports
If such supports are formed due to beams which justify fixity at the
support of slabs, then the effects on the supporting beam, such as, the
bending of the web in the transverse direction of the beam and the
torsion in the longitudinal direction of the beam, wherever applicable,
shall also be considered in the design of the beam

62. Slabs Spanning in Directions at Right Angles
The slabs spanning in two directions at right angles
and carrying uniformly distributed load may be designed by
any acceptable theory or by using coefficients given in
Annex D.
For determining bending moments in slabs spanning in two
directions at right angles and carrying concentrated load,
any accepted method approved by the engineer-in-charge
may be adopted.

63. Loads on supporting Beams

64. COMPRESSION MEMBERS
A compression member may be considered as short when
both the slenderness ratios Lx/b and Ly/ D are less than 12.
Column or strut is a compression member, the effective
length of which exceeds three times the least lateral
dimension.

65. Effective Length of Compression Members
To determine whether a column is a no sway or a sway
column, stability index Q may be computed as given below :

66. Remarks
• It is found that when Q < 0.04, the P- effects are less
than 5% of the first order effects.
• In the absence of detailed analysis, the lateral
flexibility measure of the storey u / Hu , (storey drift
per unit storey shear) may be taken as (for a typical
intermediate storey):
• u / Hu = hs /(12 E (Ic/hs) + hs /(12 E (Ib/lb)
• Where Ic = Sum of moment of inertial of all columns
in the storey,
Ib/lb = Sum of ratios of I to span of all floor beams in
the storey & E = Modulus of Elasticity

67. Effective Length of Compression Members

68. Effective Length of Compression Members

69. Effective Length of Compression Members









btx
yy
uc
yy
c
yy
uc
yy
c
1
K
K
K
K
K
β









btx
yy
lc
yy
c
yy
lc
yy
c
2
K
K
K
K
K
β
BtX1
BtY1
BbX1
LC = Lower
Column
C = Column
Considered
UC = Upper Column
L
=
Unsupported
Length
BbY1
Beam stiffness in 'No Sway' frames = EI/2L.
For 'Sway' frames, beam stiffness = 1.5EI/L.
(Ref.: Appendix D, SP:24-1983, Explanatory
Handbook on IS:456-1978)

70. Slenderness Limits for Columns
The unsupported length between end
restraints shall not exceed 60 times the least
lateral dimension of a column.

71. Minimum Eccentricity
All columns shall be designed for minimum
eccentricity, equal to the unsupported length
of column/500 plus lateral dimensions/30,
subject to a minimum of 20 mm.
Where bi-axial bending is considered, it is
sufficient to ensure that eccentricity exceeds
the minimum about one axis at a time.

72. Development Length of Bars

73. Design bond stress
• Design bond stress in limit state method for plain bars
in tension shall be as below:
Grade of Concrete: M20 M25 M30 M35 > M40
Design bond stress 1.2 1.4 1.5 1.7 1.9
For deformed bars conforming to IS 1786 these values shall be
increased by 60 percent.
For bars in compression, the values of bond stress for bars in tension
shall be increased-by 25 percent.

74. Lap Splices
• Lap length including anchorage value of hooks for
bars in flexural tension shall be Ld or 30 wherever is
greater and for direct tension shall be 2Ld or 30
whichever is greater. The straight length of the lap
shall not be less than 15 or 200mm.

75. Lap Splices

76. Lap Splices

77. Lap Splices

78. Curtailment of Tension Reinforcement in
Flexural Members
Positive moment reinforcement
• At least one-third the positive moment reinforcement in
simple members and one fourth the positive moment
reinforcement in continuous members shall extend along the
same face of the member into the support, to a length equal
to L,/3
Negative moment reinforcement
• At least one-third of the total reinforcement provided for
negative moment at the support shall extend beyond the
point of inflection for a distance not less than the effective
depth of the member of 12 dia or one-sixteenth of the clear
span whichever is greater.

79. Maximum distance between Bars in tension
• Slabs
• The horizontal distance between parallel
reinforcement bars shall not be more than three
times the effective depth of solid slab or 300mm
(450 mm in earlier version), whichever is
smaller.

80. Spacing of Reinforcement
Minimum Distance Between Individual Bars
Spacing of main reinforcing bars shall usually be not-
less than the greatest of the following:
• The diameter of the bar if bars are of equal
diameter
• The diameter of the larger bar if the diameters are
unequaI
• 5 mm more than the nominal maximum size of
coarse aggregate

81. Maximum Distance Between Bars in Tension

82. Nominal Cover to Reinforcement
• Nominal cover is the
design depth of concrete
cover to all steel
reinforcement, including
links. It is the dimension
used in the design and
indicated in the drawing.
It shall not be less than
diameter of bar.

83. Nominal cover to meet durability requirement

84. Nominal cover to meet durability requirement

85. Comments
• For footings minimum cover shall be 50mm
• Inside slab and beams may have 20mm nominal
cover as against outside beams and roof, where
nominal cover will be 30mm.
• IS specifies+10mm deviation in cover. As more
cover means less effective depth and more
steel required, this may be taken into account
while calculating the steel.
• The water retaining structures whether to
consider under severe or moderate exposure
condition?

86. Fire Resistant

87. Fire Resistant

88. Requirements of Reinforcement for Structural Members
Tension reinforcement

89. Compression reinforcement
The maximum area of compression reinforcement
shall not exceed 0.04 bD.
Compression reinforcement in beams shall be
enclosed by stirrups for effective lateral restraint.

90. Side face reinforcement
• Where the depth of the web in a beam exceeds 750
mm, side face reinforcement shall be provided
along the two faces.
• The total area of such reinforcement shall be not
less than 0.1 percent of the web area and shall be
distributed equally on two faces at a spacing not
exceeding 300 mm or web thickness whichever is
less.
Diameter of bar > Sb b /fy

91. slabs
• The mild steel reinforcement in either direction in
slabs shall not be less than 0.15 percent of the total
cross sectional area. However, this value can be
reduced to 0.12 percent when high strength
deformed bars or welded wire fabric are used.
• The diameter of reinforcing bars shall not exceed
one eight of the total thickness of the slab.

92. Maximum Spacing of Shear Reinforcement
• The maximum spacing of shear reinforcement
measured along the axis of the member shall not
exceed 0.75d for vertical stirrups and d for
inclined stirrups at 45, where d is effective
depth of the section. In no case shall the
spacing exceed 300mm

93. Minimum Shear Reinforcement
• Minimum shear reinforcement in the form of stirrups
shall be provided such that:
Asv /b Sv  0.4 /0.87 fy
Where,
• Asv = total c/s area of stirrups legs effective in shear
• Sv = Stirrup spacing along the length of member
• B = Width of the beam or breadth of web of flanged
beam
• Fy = Characteristic strength of stirrup reinforcement in
N/mm2 which shall not taken greater than 415 N/mm2.

94. Expansion Joint
• Normally structures exceeding 45m in lengths are
designed with one or more expansion joints. However in
view of the large number of factors involved in deciding
the location, spacing and nature of expansion joint, the
provision of expansion joint should be left to the
discretion of the designer. IS 3414 gives the design
considerations, which need to be examined and
provided for.

95. Footings
• Nominal Reinforcement
• Minimum reinforcement and spacing shall be as per
the requirement of solid slab.
• The nominal reinforcement for concrete section
of thickness greater than 1m shall be 360 mm2
per metre length in each direction on each face.
This provision does not supersede the
requirement of minimum tensile reinforcement
based on the depth of the section.

96. Footings

97. Footings

98. Structural Design (Limit State Method)
Cracking
• Cracking of concrete should adversely affect the
appearance or durability of the structure; the acceptable
limits of cracking would very with the type of structure
and environment. Where specific attention is required to
limit the designed crack width to a particular value,
crack width calculation may be done using formulae in
Annex F.

99. Cracks
• The surface width of the cracks should not, in general,
exceed 0.3mm in members where cracking is not
harmful and does not have any serious adverse effects
upon the preservation of reinforcement steel nor upon
the durability of the structures.
• In members where cracking in tensile zone is harmful
either because they are exposed to the effects of the
weather or continuously exposed to moisture or in
contact soil or ground water, an upper limit of 0.2mm is
suggested for the maximum width of cracks.
• For particularly aggressive environment, such as the
‘severe’ category in Table 3, the assessed surface width
of cracks should not in general exceed 0.1mm.

100. Example-1: Find the maximum probable crack width for
the one way slab designed as below:
Span = 4.0m Total Thickness = 185mm Effective depth d = 185-
20-10/2=160mm
M dl+ll under service condition = 20 kNm
Reinforcement : 10 @ 125 c/c
%steel = 0.3927 p=0.003927 Ast = 628.32 sqmm
fck = 20 Mpa fy = 415 MPA
cbc =7 N/sqmm st = 230 N/sqmm
modular ratio = 280/(3 cbc) = 13.33

101. Example-1: Cont.
Calculation of Depth of Neutral axis : Nd
Pm = 0.003927x13.33 = 0.052347
A =  2(pm)+(pm)(pm) = 0.32777
N = A - (pm)
= 0.2754
Nd = 0.2754x160 = 44mm
Calculation of tensile stress in steel under service load: fst
fst = [M (d-Nd) / Icr ] m
Icr = b (Nd)^3 /3 + m Ast (d-nd)^2
= 141095470 mm^4
fst = 219 N/sqmm

102. Example-1: Cont.
Calculation of Strain
e1 = Strain at the level considered, calculated ignoring the stiffening of
the concrete in the tension zone
= fst/Es [(D-Nd)/(d-nd)]
= 219/2e5 [(185-44)/(160-44)]
=0.001331
Calculation for Crackwidth
Cover Cmin = 20mm Spacing/2 = 125/2=62.5mm
acr = 20x20 + 62.5x62.5 = 65.623mm
b(h-x)(a-x)
em = e1 - -----------------
3 Es As (d-x)
=0.001331 – 1000(185-44)(185-44)/[3x2e5x628.32(160-44)]
= 0.00087638

103. Example-1: Cont.:
3 acr em
Wcr = ------------------------------
1 + 2 (acr-Cmin)
-----------------
h-x
= 0.10261mm
Example-2:
If 8 @ 80c/c is used then Wcr = 0.070mm
Example-3:
If 12 @ 180c/c is used then Wcr = 0.14416mm

104. Lateral Sway
• Under transient wind load the lateral sway at the top
should not exceed H/500, where H is the total height of
the building. For seismic loading, reference should be
made to IS 1893.

105. columns
The cross-sectional area of longitudinal reinforcement, shall
be not less than 0.8 percent nor more than 6 percent of the
gross cross sectional area of the column.
The bars shall not be less than 12 mm in diameter. The bars
shall not be less than 12 mm in diameter.
Spacing of longitudinal bars measured along the periphery
of the column shall not exceed 300 mm.

106. columns

107. Pitch and diameter of lateral ties
1) Pitch-The pitch of transverse reinforcement shall be
not more than the least of the following distances:
i) The least lateral dimension of the compression members;
ii) Sixteen times the smallest diameter of the longitudinal
reinforcement bar to be tied; and
iii) 300 mm.
2) Diameter-The diameter of the polygonal links or
lateral ties shall be not less than one fourth of the diameter
of the largest longitudinal bar, and in no case less than 6
mm.

108. WALLS
Reinforced concrete walls subjected to direct
compression or combined flexure and direct
compression should be designed in accordance with
Section 5 or Annex B provided the vertical reinforcement
is provided in each face.
Braced walls subjected to only vertical compression may
be designed as per empirical procedure given in 32.2.
The minimum thickness of walls shall be 100 mm.

109. Empirical Design Method for Walls Subjected
to Inplane Vertical Loads
Braced Walls
Walls or vertical braced elements are arranged in two directions so as
to provide lateral stability to the structure as a whole.
a. Lateral forces are resisted by shear in the planes of these walls or
by braced elements.
b. Floor and roof systems are designed to transfer lateral forces.
c. Connections between the wall and the lateral supports are
designed to resist a horizontal force not less than
1) the simple static reactions to the total applied horizontal forces at
the level of lateral support; and
2) 2.5 percent of the total vertical load that the wall is designed to
carry at the level of lateral support.

110. Eccentricity of Vertical Load
The design of a wall shall take account of the actual
eccentricity of the vertical force subject to a minimum value
of 0.05 t.
The vertical load transmitted to a wall by a discontinuous
concrete floor or roof shall be assumed to act at one-third
the depth of the bearing area measured from the span
face of the wall.

111. Effective Height
The ratio of effective height to thickness, Hw/t shall not
exceed 30.
The effective height of a braced wall shall be taken as
follows:
a) Where restrained against rotation at both ends by
1) floors 0.75 Hw or
2) intersecting walls or similar members 0.75 L ,
whichever is the lesser.
b) Where not restrained against rotation at both ends by
1) floors 1.0 H, or
2) intersecting walls or similar-members 1.0 L,
whichever is the lesser.

112. Design Axial Strength of Wall
The design axial strength Puw per unit length of a
braced wall in compression may be calculated from the
following equation:

113. Design for Horizontal Shear
The critical section for maximum shear shall be taken at a
distance from the base of 0.5 Lw or 0.5 H, whichever is
less,
The nominal shear stress vw in walls shall be
obtained as follows: vw = Vu I t.d
Under no circumstances shall the nominal shear stress
vw in walls exceed 0.17 fck in limit state method and
0.12 fck in working stress method.

114. Design Shear Strength of Concrete

115. Design of Shear Reinforcement

116. Minimum Requirements for Reinforcement
in Walls

117. SECTION 5 STRUCTURAL DESIGN
(LIMIT STATE METHOD)

118. Introduction to IS 456:2000 :-
Limit State Method (LSM)
• The LSM ensures the safety at ultimate load and serviceability at
working load rendering the structure fit for its intended use.
• The salient features and the merits of LSM;
1. It consider the actual behaviour of structure during the entire
loading history up to collapse.
2. It adopts the concept of fitness of structure to serve the desired
function during the service life span and defines the limiting state
of fitness as the “Limit State”
3. It attempts to define quantitatively the margins of safety or fitness
on some scientific mathematical (derived from classical reliability
theory and statistical probability) foundations rather than on
adhoc basis of experience and judgment

119. TYPES AND CLASSIFICATION OF LIMIT
STATE
I) Limit State of Collapse (Ultimate Limit state)
: Design to this limit state ensures safety of
structure from collapse.

120. LIMIT STATE OF COLLAPSE : FLEXURE

121. (II) Limit State of Serviceability
A) Limit State of Deflection : Design to this limit state
safeguard the serviceability of structure from
adverse effects of excessive deflection :creates
feeling of lack of safety, affects geometry & Shape
hence appearance of structure.
B) Limit State of Cracking : Design to this limit state
safeguard the serviceability of structure from
adverse effects of excessive cracking

122. Other Limit state
Structures designed for special or unusual functions
need consideration of appropriate Limit States.
They are
(i) Vibrations
(ii) Fire resistance
(iii) Durability

123. Partial Safety Factors

124. Thank You
REMEMBER
Prevention is better than cure.