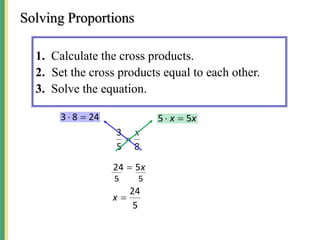
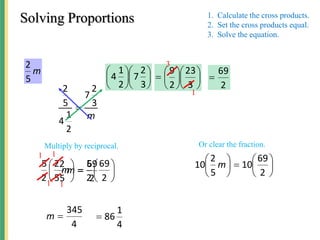
This document discusses ratios, proportions, and similar figures. It begins by defining a ratio as a comparison of two quantities using a fraction. It then provides examples of writing and interpreting ratios and unit ratios. The document explains that a proportion is when two ratios are set equal, and proportions can be solved using cross-multiplication. Examples are given for solving various types of proportion problems. The document concludes by defining congruent angles and similar figures, and providing examples of using proportions to solve for missing lengths in similar figures.

1. Ratios and Proportions
3.1
1. Solve problems involving ratios.
2. Solve for a missing number in a proportion.
3. Solve proportion problems.
4. Use proportions to solve for missing lengths in figures
that are similar.
You may use calculators in this chapter!!

2. Ratio: A comparison of two quantities
using a quotient (fraction).
The word to separates the numerator and
denominator quantities.
The ratio of 12 to 17 translates to
12
17
.
Numerator Denominator
Unit ratio: A ratio with a denominator of 1.

3. A bin at a hardware store contains 120 washers
and 85 bolts. Write the ratio of washers to bolts in
simplest form.
Ratios
The ratio of washers to bolts bolts
washers

85
120

17
24

Express the ratio as a unit ratio. Interpret the answer.
17
24
1
41
1.

There are 1.41 washers for every bolt.

4. The price of a 10.5 ounce can of soup is $1.68. Write
the unit ratio that expresses the price to weight.
Ratios
The ratio of price to weight
weight
price

10.5
1.68

1
16
.

Interpret the answer.
The soup costs $.16 per ounce.

5. One molecule of glucose contains 6 carbon atoms, 12
hydrogen atoms, and 6 oxygen atoms. What is the
ratio of hydrogen atoms to the total number of atoms
in the molecule?
Ratios
The ratio of hydrogen atoms to total atoms
atoms
total
atoms
hydrogen
24
12

2
1


6. Proportions
4
3
8
6

Proportion: two ratios set equal.
24
6
4 
 24
8
3 

Cross-products of proportions are always equal!
Only works if there is an equal (=) sign!
4
3
8
6
 No!

7. Solving Proportions
1. Calculate the cross products.
2. Set the cross products equal to each other.
3. Solve the equation.
8
5
3 x

24
8
3 
 x
x 5
5 

x
5
24 
5
5
5
24

x

8. Solving Proportions
x
18
20
12

x
x 12
12 
 360
18
20 

360
12 
x
12
12
30

x
1. Calculate the cross products.
2. Set the cross products equal.
3. Solve the equation.

9. Solving Proportions
m
3
2
7
2
1
4
5
2

m
5
2












3
2
7
2
1
4
2
69
5
2

m
4
345

m
1. Calculate the cross products.
2. Set the cross products equal.
3. Solve the equation.













3
23
2
9
2
69














2
69
10
5
2
10 m













2
69
2
5
5
2
2
5
m
1
1
1
1
3
1
4
1
86

Multiply by reciprocal. Or clear the fraction.

10. Solving Proportions
3
7
6
5


x
 
5
3 
x 42
  42
5
3 

x
3
3
9

x
1. Calculate the cross products.
2. Set the cross products equal.
3. Solve the equation.
42
15
3 

x
15
15 

27
3 
x

11. Solving Proportions
Gary notices that his water bill was $24.80 for 600
cubic feet of water. At that rate, what would the
charges be for 940 cubic feet of water?
feet
cubic
dollars

600
80
24.
23312 x
600
x
600
23312 
600
600
85
38.
$
x 
940
x

12. Solving Proportions
Chevrolet estimates that its 2012 Tahoe will travel
520 miles on one tank of gas. If the tank of the
Tahoe holds 26 gallons, how far can a driver expect
to travel on 20 gallons?
gallon
miles

26
520
10400 x
26
x
26
10400 
26
26
miles
400

x
20
x

13. Congruent angles: Angles that have the same measure.
The symbol for congruent is .

Similar figures: Figures with congruent angles and
proportional side lengths.
The two figures are similar. Find the missing length.
10
8
6
5
x
small
large 
5
10
x
10 40
40
10 
x
10
10
4

x
x
8

14. Similar Figures
The two figures are similar. Find the missing lengths.
Round your answer to the nearest hundredth.
small
large

5
6
8
12
.
.
4
134. x
.5
6
x
.
. 5
6
4
134 
5
6
5
6 .
.
km
68
20.
x 
5
10.
x
12.8 km
10.5 km
6.5 km 6.5 km
4.6 km
x
y

5
6
8
12
.
.
88
58. y
.5
6
y
.
. 5
6
88
58 
5
6
5
6 .
.
km
06
9.
y 
6
4.
y