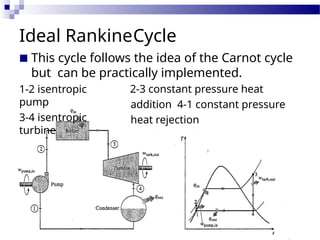
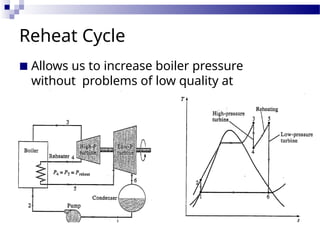
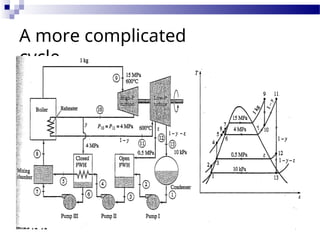
The document reviews the Rankine cycle and its application of the first law of thermodynamics, emphasizing the importance of isentropic processes in ideal cycles. It outlines the differences between ideal and real cycles, highlighting how deviations affect efficiency and performance due to factors like pressure drops and non-ideal pump and turbine behaviors. Additionally, it discusses strategies for improving system efficiency, such as lowering condenser pressure and utilizing superheating.