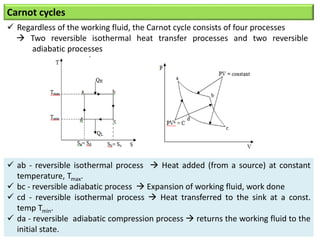
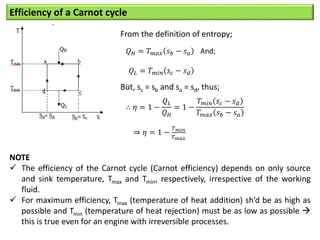
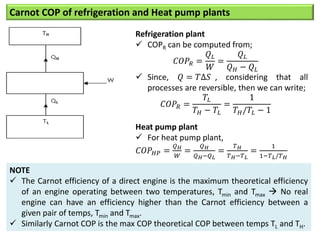
- The Carnot cycle consists of four processes: two reversible isothermal heat transfer processes and two reversible adiabatic processes. - The efficiency of the Carnot cycle depends only on the source and sink temperatures, irrespective of the working fluid. Maximum efficiency is achieved with highest source temperature and lowest sink temperature. - The Carnot COP is the maximum theoretical COP between two temperatures for refrigeration or heat pump cycles. No real system can exceed the Carnot COP.

2. Carnot cycles
 Regardless of the working fluid, the Carnot cycle consists of four processes
 Two reversible isothermal heat transfer processes and two reversible
adiabatic processes
 ab - reversible isothermal process  Heat added (from a source) at constant
temperature, Tmax.
 bc - reversible adiabatic process  Expansion of working fluid, work done
 cd - reversible isothermal process  Heat transferred to the sink at a const.
temp Tmin.
 da - reversible adiabatic compression process  returns the working fluid to the
initial state.

3. Efficiency of a Carnot cycle
From the definition of entropy;
And;
𝑄𝐻 = 𝑇𝑚𝑎𝑥 𝑠𝑏 − 𝑠𝑎
𝑄𝐿 = 𝑇𝑚𝑖𝑛 𝑠𝑐 − 𝑠𝑑
But, sc = sb and sa = sd, thus;
∴ 𝜂 = 1 −
𝑄𝐿
𝑄𝐻
= 1 −
𝑇𝑚𝑖𝑛 𝑠𝑐 − 𝑠𝑑
𝑇𝑚𝑎𝑥 𝑠𝑏 − 𝑠𝑎
⇒ 𝜂 = 1 −
𝑇𝑚𝑖𝑛
𝑇𝑚𝑎𝑥
NOTE
 The efficiency of the Carnot cycle (Carnot efficiency) depends on only source
and sink temperature, Tmax and Tmin, respectively, irrespective of the working
fluid.
 For maximum efficiency, Tmax (temperature of heat addition) sh’d be as high as
possible and Tmin (temperature of heat rejection) must be as low as possible 
this is true even for an engine with irreversible processes.

4. Carnot COP of refrigeration and Heat pump plants
Refrigeration plant
 COPR can be computed from;
𝐶𝑂𝑃𝑅 =
𝑄𝐿
𝑊
=
𝑄𝐿
𝑄𝐻 − 𝑄𝐿
 Since, 𝑄 = 𝑇∆𝑆 , considering that all
processes are reversible, then we can write;
𝐶𝑂𝑃𝑅 =
𝑇𝐿
𝑇𝐻 − 𝑇𝐿
=
1
𝑇𝐻/𝑇𝐿 − 1
Heat pump plant
 For heat pump plant,
𝐶𝑂𝑃𝐻𝑃 =
𝑄𝐻
𝑊
=
𝑄𝐻
𝑄𝐻−𝑄𝐿
=
𝑇𝐻
𝑇𝐻−𝑇𝐿
=
1
1−𝑇𝐿/𝑇𝐻
NOTE
 The Carnot efficiency of a direct engine is the maximum theoretical efficiency
of an engine operating between two temperatures, Tmin and Tmax  No real
engine can have an efficiency higher than the Carnot efficiency between a
given pair of temps, Tmin and Tmax.
 Similarly Carnot COP is the max COP theoretical COP between temps TL and TH.

5. Examples 6.1
1. A Carnot heat engine receives 500 kJ of heat per cycle from a high –
temperature source at 6250C and rejects heat to a low – temperature sink at
300C. Determine:
(i) The thermal efficiency of this Carnot engine. (67.2%)
(ii) The amount of heat rejected to the heat sink per cycle. (164 kJ)
2. An investor claims to have developed a refrigerator that maintains the
refrigerated space at 350F while operating in a room where the temperature is
750F and has a COP of 13.5. Is this claim reasonable?
3. A heat pump maintains a house at a fixed temperature. The house is to be
maintained at 210C at all times. The house is estimated to be losing heat at a rate
of 135,000 kJ/h when the outside temperature drops to -50C. Determine the
minimum power required to drive this heat pump. (3.32 kW)

6. Steam power plants
The Carnot vapor cycle
 1 -2: Fluid is heated reversibly and
isothermally in the boiler
 2 -3: fluid is expanded isentropically in
a turbine
 3 – 4: fluid is condensed reversibly and
isothermally in a condenser
 4 – 1: fluid is compressed isentropically
by a compressor to the initial state
Impracticalities (limitations) of the Carnot vapor cycle
 Process 1 – 2 has to be limited to the 2- phase region, this limits the maximum
possible temperature to 3740C (critical temp of water)  This limits the cycle’s
efficiency in turn.
 Turbine handles steam of low dryness fraction (steam with high moisture
content)  impigement of water droplets on turbine blades increases rate of
erosion, hence increased blades wear and thus high replacement costs
 Compression handles a 2 – phase steam; hard to design a compressor that
handles both liquid and vapor. Its also hard to control the condesation process
to end exactly at point 4.

7. Rankine cycle
 Addresses the limitations of the Carnot vapour cycle
 Rankine cycle is the ideal for the vapour power and refrigeration cycles
Processes of the ideal Rankine vapour cycle
 1 – 2: Isentropic compression in a pump
 2 – 3: Constant pressure heat addition in the boiler.
 3 – 4: Isentropic expansion in the turbine.
 4 – 1: Constant pressure heat rejection in the condenser

8. Analysis of the Ideal Rankine cycle
Assumption
 Changes in Potential and Kinetic Energies are always neglected
Boiler
 Water enters the boiler as a compressed liquid
at state 2
 Usually water leaves superheated
 We assume heat is added to vaporizing water at
a constant pressure
 Amount of heat added, 𝑄23 = 𝑚 ℎ3 − ℎ2
Turbine
 Steam (always superheated at boiler pressure) enters turbine and expanded
isentropically to state 4 (corresponding the condenser pressure)
 Work is generated by the turbine, which drives a generator for power
production.
 There is negligable heat transfer in the turbine, 𝑄34 ≈ 0
 Using SFEE, work delivered by turbine, 𝑊𝑇 = 𝑚 ℎ3 − ℎ4

9. Analysis of the Ideal Rankine cycle cont’d
Condenser
 Steam at state 4 is condensed at constant
pressure.
 Condenser is a heat exchanger, rejecting heat
to a cooling medium
 Water leaves as a saturated liquid at state 1
 The rate of heat rejection, 𝑄41 = 𝑚 ℎ4 − ℎ1
Pump
 Raises the water pressure from condenser pressure (P1 = P4) to boiler pressure
(P2 = P3)
 Magnitude of power input to the pump, 𝑊𝑃 = 𝑚 ℎ2 − ℎ1
 The power input to a reversible pump can also be computed from,
ℎ2 − ℎ1 = 𝑣1 𝑃2 − 𝑃1 , where v1 = specific volume at 1. (Proof in
lecture notes)
NOTE
 The pump power input is normally very small compared to the power output
from the turbine and is usually neglected in comparison to the latter
 If pump power is negligible, then; ℎ2 − ℎ1 ≈ 0 ⇒ ℎ2 ≈ ℎ1

10. Rankine cycle thermal efficiency
Rankine cycle efficiency can be obtained from;
𝜂𝑡ℎ =
𝑛𝑒𝑡 𝑤𝑜𝑟𝑘 𝑜𝑢𝑡𝑝𝑢𝑡
ℎ𝑒𝑎𝑡 𝑠𝑢𝑝𝑝𝑙𝑖𝑒𝑑 𝑡𝑜 𝑏𝑜𝑖𝑙𝑒𝑟
 Net work output, 𝑊𝑛𝑒𝑡 = 𝑊𝑡𝑢𝑟𝑏𝑖𝑛𝑒 − 𝑊
𝑝𝑢𝑚𝑝
∴ 𝜂𝑡ℎ =
𝑊𝑇−𝑊𝑃
𝑄32
=
ℎ3−ℎ4 − ℎ2−ℎ1
ℎ3−ℎ2
’
Actual Rankine cycle
 Actual vapour cycles differ from ideal Rankine cycles due to irreversibiities such
as friction and heat transfer across boundaries
 Fluid friction causes pressure drops in the boiler,
and the piping between various components
 Steam leaves the boiler at slightly lower
pressure (2 – 3)
 Hence water must be pumped to higher
pressures to cater for these losses, hence
larger pump power input.
 The pump and turbine aren't isentropic as the
case of the ideal cycle

11. Analysis of the actual Rankine cycle
 The pressure drops are very small (less than 3%)  always neglected.
 Losses in pump and turbine are significant
 Always taken care of using isentropic efficiency
 If,
t – isentropic efficiency of the turbine, and,
p – isentropic efficiency of the pump, then;
𝜂𝑡 =
𝐴𝑐𝑡𝑢𝑎𝑙 𝑤𝑜𝑟𝑘 𝑜𝑢𝑡𝑝𝑢𝑡
𝐼𝑠𝑒𝑛𝑡𝑟𝑜𝑝𝑖𝑐 𝑤𝑜𝑟𝑘 𝑜𝑢𝑡𝑝𝑢𝑡
=
𝑚 ℎ3−ℎ4
𝑚 ℎ3−ℎ4𝑠
=
ℎ3−ℎ4
ℎ3−ℎ4𝑠
𝜂𝑝 =
𝐼𝑠𝑒𝑛𝑡𝑜𝑝𝑖𝑐 𝑤𝑜𝑟𝑘 𝑖𝑛𝑝𝑢𝑡
𝐴𝑐𝑡𝑢𝑎𝑙 𝑤𝑜𝑟𝑘 𝑖𝑛𝑝𝑢𝑡
=
𝑚 ℎ2𝑠−ℎ1
𝑚 ℎ2−ℎ1
=
ℎ2𝑠−ℎ1
ℎ2−ℎ1
1 – 2: Irreversible compression process - pump
2 – 3: Heat addition process in the boiler -
considered a constant pressure process
3 – 4: Irreversible expansion process - turbine.
4 – 1: A heat rejection process in the condenser -
considered a constant pressure process

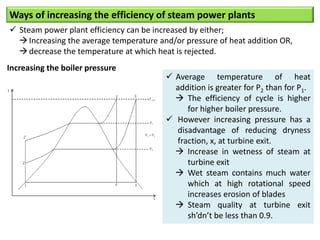
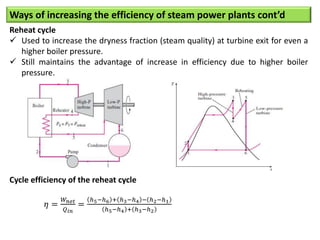
12. Other criteria used in comparing steam power plants
Efficiency ratio
 Ratio of the actual cycle efficiency to Rankine efficiency
 Sh’d be as large as possible, the closer it is to 1.0 , the less is the energy wasted
against irreversibilities.
Work ratio
𝑊𝑜𝑟𝑘 𝑟𝑎𝑡𝑖𝑜 =
𝑁𝑒𝑡 𝑤𝑜𝑟𝑘
𝑔𝑟𝑜𝑠𝑠 𝑤𝑜𝑟𝑘
=
𝑊𝑜𝑟𝑘 𝑡𝑢𝑟𝑏𝑖𝑛𝑒−𝑊𝑜𝑟𝑘 𝑝𝑢𝑚𝑝
𝑊𝑜𝑟𝑘 𝑡𝑢𝑟𝑏𝑖𝑛𝑒
Specific steam consumption (ssc)
 It relates the plant output to the steam that is flowing through it
 Amount of steam flow also indicates the size of the components  measure of
relative sizes of the steam plants.
𝑠𝑠𝑐 =
3600
𝑊𝑛𝑒𝑡
, where Wnet – network output [kJ/kg]

13. Ways of increasing the efficiency of steam power plants
 Steam power plant efficiency can be increased by either;
Increasing the average temperature and/or pressure of heat addition OR,
decrease the temperature at which heat is rejected.
Increasing the boiler pressure
 Average temperature of heat
addition is greater for P2 than for P1.
 The efficiency of cycle is higher
for higher boiler pressure.
 However increasing pressure has a
disadvantage of reducing dryness
fraction, x, at turbine exit.
 Increase in wetness of steam at
turbine exit
 Wet steam contains much water
which at high rotational speed
increases erosion of blades
 Steam quality at turbine exit
sh’dn’t be less than 0.9.

14. Ways of increasing the efficiency of steam power plants cont’d
Reheat cycle
 Used to increase the dryness fraction (steam quality) at turbine exit for even a
higher boiler pressure.
 Still maintains the advantage of increase in efficiency due to higher boiler
pressure.
Cycle efficiency of the reheat cycle
𝜂 =
𝑊𝑛𝑒𝑡
𝑄𝑖𝑛
=
ℎ5−ℎ6 + ℎ3−ℎ4 − ℎ2−ℎ1
ℎ5−ℎ4 + ℎ3−ℎ2

15. Ways of increasing the efficiency of steam power plants cont’d
Lowering condenser pressure
 Lowering condenser pressure, lowers the
temperature of heat rejection, Tmin  increase in
efficiency.
 Coloured area on Fig. indicates increase in net work
as a result of reducing condenser pressure from P4
to P4’.
 Heat added in boiler also increases but by a smaller
value.
Super heating the steam to high temperatures
 Super heating steam to higher temp before turbine
inlet increases average heat addition temperature
 Increases both the turbine work output and heat
input in the boiler. The former is higher and hence
overall effect is increase in efficiency
 Superheating also improves the steam quality at
turbine exit (from 4 to 4’)
 Due to metallurgical properties, limit to steam temp =
620oC

16. Examples 6.2
1. A steam power plant operates on a simple ideal Rankine cycle between
pressure limits of 3 MPa and 50 kPa. The temperature of the steam at the
turbine inlet is 4500C, and the mass flow rate of steam through the cycle is 40
kg/s. Show the cycle on a T –s diagram with respect to saturation lines, and
determine:
(i) The thermal efficiency of the cycle (29.3%)
(ii) The net power output of the power plant. (35.17 MW)
2. A power plant which operates on a Rankine cycle with steam as the working fluid
operates at a boiler pressure of 40 bar and a condenser pressure of 0.1 bar. If
the temperature at the turbine inlet is 4000C, and the isentropic efficiencies of
the turbine and the pump are 80% and 90% respectively, find:
(i) The thermal efficiency (25.5%)
(ii) Work ratio of the plant (0.994)