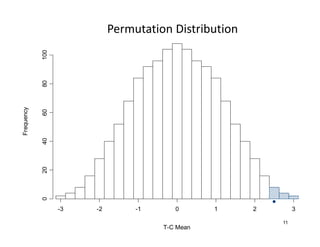
1) Permutation tests condition on all data except treatment assignments and have a valid null distribution even if test statistics or aspects of the study design are adapted based on interim blinded data. 2) For a one-sample matched pairs design, the permutation distribution of the test statistic is normal with mean 0 and variance equal to the sum of squared differences between pairs. 3) The t-statistic calculated from such a design has the same null distribution as the permutation test statistic and remains valid for interim adaptations.

1. Blinded Adaptations,
Permutation Tests & T‐Tests
Michael Proschan (NIAID)Michael Proschan (NIAID)

2. IntroductionIntroduction
• Joint work with Ekkehard Glimm and MartinJoint work with Ekkehard Glimm and Martin
Posch 2014, Stat. in Med. online
• See also Posch & Proschan 2012, Stat. in Med.
31 4146 415331, 4146‐4153

3. IntroductionIntroduction
• Clinical trials are pre‐meditated!Clinical trials are pre meditated!
• We pre‐specify everything
S i it / i f i it– Superiority/noninferiority
– Population (inclusion/exclusion criteria)
– Primary endpoint
– Secondary endpoints
– Analysis methods
– Sample size/power

4. IntroductionIntroduction
• Changes made after seeing data are rightlyChanges made after seeing data are rightly
questioned: are investigators trying to get an
unfair advantage?
– Changing primary endpoint because another
endpoint has a bigger treatment effect
– Increasing sample size because the p‐value is close
– Changing primary analysis because “assumptions
are violated”are violated
– Changing population because of promising
subgroup resultssubgroup results

5. IntroductionIntroduction
• What’s the harm? 0 05 is arbitrary anywayWhat s the harm? 0.05 is arbitrary anyway
• Problem: if unlimited freedom to change
anything the real error rate could be hugeanything, the real error rate could be huge
• Reminiscent of Bible code controversy
– Clairvoyant messages such as “Bin Laden” and
“twin towers” by skipping letters in Old Testament
– Similar messages can be found by skipping letters
in any large book (Brendan McKay)

6. IntroductionIntroduction
• But changes made before unblinding areBut changes made before unblinding are
different
• Under strong null hypothesis that treatment• Under strong null hypothesis that treatment
has NO effect, blinded data give no info about
treatment effecttreatment effect
– Impossible to cheat even if it seems like cheating
E if bli d d d t h bi d l di t ib ti it• E.g., even if blinded data show bimodal distribution, it
is not caused by treatment if strong null is true

7. Permutation TestsPermutation Tests
• Permutation tests condition on all data otherPermutation tests condition on all data other
than treatment labels
• Under strong null (D Z ) are independent• Under strong null, (D,Z ) are independent,
where Z are ±1 treatment indicators & D are
datadata
– Observed data D would have been observed
regardless of the treatment givenregardless of the treatment given
– It is as if we observed D FIRST, then made the
treatment assignments Ztreatment assignments Z

8. Permutation TestsPermutation Tests
• Peaking at data changes nothing becausePeaking at data changes nothing because
permutation tests already condition on D
• Conditional distribution of test statistic T(Z Y)• Conditional distribution of test statistic T(Z,Y)
given D is that of T(Z,y) where y is fixed
Di ib i f Z d d d i i• Distribution of Z depends on randomization
method
– Simple
– Permuted block, etc.

9. Permutation TestsPermutation Tests
T T C C C T C T C C T T C T T C
4 8 4 0 1 3 0 4 4 0 2 5 0 2 1 0
T-C T-C T-C T-C
O ll T C
4.0 3.0 1.5 1.5
Overall T-C
2.5

10. Permutation TestsPermutation Tests
T C C T C T C T T T C C C T C T
4 8 4 0 1 3 0 4 4 0 2 5 0 2 1 0
T-C T-C T-C T-C
O ll T C
-4.0 3.0 -1.5 0.5
Overall T-C
-0.5

11. Rerandomization Distribution
Permutation Distribution
100
y
80
Frequency
06004002
11
T-C Mean
-3 -2 -1 0 1 2 3

12. Blinded 2‐Stage ProceduresBlinded 2 Stage Procedures
• Blinded 2‐stage adaptive procedures use 1stBlinded 2 stage adaptive procedures use 1st
stage to make design changes
– Sample size (Gould, 1992, Stat. in Med. 11, 55‐66; p ( , , , ;
Gould & Shih, 1992 Commun. in Stat. 21, 2833‐
2853)
P i d i ( di li li– Primary endpoint (e.g., diastolic versus systolic
blood pressure)
• Previous argument shows that if adaptation is• Previous argument shows that if adaptation is
made before unblinding, a permutation test
on 1st stage data is still validon 1st stage data is still valid

13. Blinded 2‐Stage ProceduresBlinded 2 Stage Procedures
• Careful! Subtle errors are possibleCareful! Subtle errors are possible
• E.g., in adaptive regression, which of the
following is (are) valid?following is (are) valid?
1. From ANCOVAs Y=β01+βz+βixi, i=1,…,k, pick xi
that minimizes MSE; do permutation test onthat minimizes MSE; do permutation test on
winner
2 From ANCOVAs Y=β 1+β x i=1 k pick x that2. From ANCOVAs Y=β01+βixi, i=1,…,k, pick xi that
minimizes MSE; do permutation test on
Y=β01+βz+β*x*, where x* is winnerβ0 β β ,

14. Blinded 2‐Stage ProceduresBlinded 2 Stage Procedures
• Careful! Subtle errors are possibleCareful! Subtle errors are possible
• E.g., in adaptive regression, which of the
following is (are) valid?following is (are) valid?
1. From ANCOVAs Y=β01+βz+βixi, i=1,…,k, pick xi
that minimizes MSE; do permutation test onthat minimizes MSE; do permutation test on
winner
2 From ANCOVAs Y=β 1+β x i=1 k pick x that2. From ANCOVAs Y=β01+βixi, i=1,…,k, pick xi that
minimizes MSE; do permutation test on
Y=β01+βz+β*x*, where x* is winnerβ0 β β ,

15. Blinded 2‐Stage ProceduresBlinded 2 Stage Procedures
• Unblinding and apparent α‐inflation also possible U b d g a d appa e t α at o a so poss b e
if strong null is false
• E.g., change primary endpoint based on “blinded” g g p y p
data (X,Y1,Y2), Y1 and Y2 are potential primaries
and X=level of study drug in blood
– X completely unblinds
– Can then pick Y1 or Y2 with biggest z‐score
Clearly inflates α– Clearly inflates α
– Problem: strong null requires no effect on ANY
variable examined (including X=level of study drug)

16. Blinded 2‐Stage ProceduresBlinded 2 Stage Procedures
• Claim: the following procedure is validClaim: the following procedure is valid
– After viewing 1st stage data D1, choose test
statistic T1(Y1 Z1) and second stage data to collectstatistic T1(Y1,Z1) and second stage data to collect
– After observing D2, choose T2(Y2,Z2) and method
of combining T1 and T2, f(T1,T2)of combining T1 and T2, f(T1,T2)
– Conditional distribution of f(T1,T2) given (D1,D2) is
its stratified permutation distributionp
– Stratified permutation test controls conditional, &
therefore unconditional type I error rate

17. Focus of Rest of TalkFocus of Rest of Talk
• Permutation tests are asymptoticallyPermutation tests are asymptotically
equivalent to t‐tests
• Suggests that adaptive t tests might be valid if• Suggests that adaptive t‐tests might be valid if
adaptive permutation tests are
W id i b• We consider connections between
permutation and t‐tests, and validity of
d i f d i iadaptive t‐tests from adaptive permutation
tests

18. One‐Sample CaseOne Sample Case
• Community randomized trials sometimes pair Co u ty a do ed t a s so et es pa
match & randomize within pairs
• E.g., COMMIT trial used community intervention g y
to help people quit smoking—11 matched pairs
• D=difference in quit rates between treatment (T)
& control (C)
T C D=T‐C
Pair i 0.30 0.25 +0.05

19. One‐Sample CaseOne Sample Case
• Community randomized trials sometimes pair Co u ty a do ed t a s so et es pa
match & randomize within pairs
• E.g., COMMIT trial used community intervention g y
to help people quit smoking—11 matched pairs
• D=difference in quit rates between treatment (T)
& control (C)
C T D=T‐C
Pair i 0.30 0.25 ‐0.05

20. One‐Sample CaseOne Sample Case
• Permuting labels changes only sign of DPermuting labels changes only sign of D
• Permutation test conditions on |Di|= di
+;
d + d d + ll lik l‐di
+ and di
+ are equally likely
• The permutation distribution of Di is dist. ofThe permutation distribution of Di is dist. of
21w p1where /ZdZ  
21w.p.1
21w.p.1where,
/
/ZdZ iii



21. One‐Sample CaseOne Sample Case
• In 1st stage, adapt based on |D1|,…,|Dn| (blinded)g , p | 1|, ,| n| ( )
– E.g., increase stage 2 sample size because |Di| is very
large
• What is conditional distribution of 1st stage sum• What is conditional distribution of 1st stage sum
ΣDi given |D1|=d1
+,…,|Dn|= dn
+ and the
adaptation?adaptation?
– The adaptation is a function of |D1|,…,|Dn|
– The null distribution of ΣDi given |D1|=d1
+,…,|Dn|= dn
+
i g | 1| 1 , ,| n| n
IS its permutation distribution
– Conclusion: permutation test on stage 1 data still valid

22. One‐Sample CaseOne Sample Case
• Mean and variance of permutationMean and variance of permutation
distribution are
    
0)(E iiii ZEddZ 
  

 222
)(var
)(
iiiii
iiii
dZEddZ

23. One‐Sample CaseOne Sample Case
• Asymptotically, permutation distribution is sy ptot ca y, pe utat o d st but o s
normal with this mean and variance (Lindeberg‐
Feller CLT)
• I.e., conditional distribution of Di given , i g
|D1|=d1
+,…,|Dn|= dn
+ is asymptotically N(0,di
2)
• Depends on |D1|=d1
+,…,|Dn|= dn
+ only through
L2=di
2L di

24. One‐Sample CaseOne Sample Case
• Asymptotically, permutation distribution ofAsymptotically, permutation distribution of
  N
d
dN
D
D
T ii
2
2
2
)1,0(
,0
' 




LD
dD ii
2


n
L
Dns
ns
D
T i
i
2
22
02
0
)/1(;'  
• Like t‐test with variance estimate s0
2 instead
of usual sample variance s2

25. One‐Sample CaseOne Sample Case
• Recap: Permutation distribution of T’ is dist ofRecap: Permutation distribution of T is dist of

 12
|||,...,|given' n
i
DD
D
D
T


2
i'
i
DT
D
 

22
2
d dtd ')10(
given' i
DLN
DT
• Conclusion: T’ is asymptotically indep of L2
  22
ondependtdoesn')1,0( iDLN

26. One‐Sample CaseOne Sample Case
• Begs question, is this true for all sample sizesBegs question, is this true for all sample sizes
under normality assumption?
• if Di are iid N(0,2), then canif Di are iid N(0, ), then can
?fti d db' 2
 i
D
D
T ?oftindependenbe' 2
2 

 i
i
i
D
D
T
• Seems crazy, but it’s true!

27. One‐Sample CaseOne Sample Case
• One way to see that T’ is independent of Di
2One way to see that T is independent of Di
uses Basu’s theorem:
• Recall S is sufficient for θ if F(y|s) does not
d d θ i i l if { ( )} f ll θdepend on θ; it is complete if E{g(S)}=0 for all θ
implies g(S)≡0 with probability 1
• A is ancillary if its distribution does not depend• A is ancillary if its distribution does not depend
on θ
• Basu, 1955, Sankhya 15, 377‐380:
If S is a complete, sufficient statistic and A
is ancillary, then S and A are independent

28. One‐Sample CaseOne Sample Case
• Consider Di iid N(0 2) with 2 unknownConsider Di iid N(0, ) with  unknown
–Di
2 is complete and sufficient
– T’= Di/(Di
2)1/2 is ancillary because it is scale‐
invariant
– By Basu’s theorem, T’ and Di
2 are independent

29. One‐Sample CaseOne Sample Case
• Same argument shows that the usual t‐Same argument shows that the usual t
statistic is independent of Di
2
2 2• Under Di iid N(0,2) with 2 unknown
–Di
2 is complete and sufficient
– Usual t‐statistic T= Di/(ns2)1/2 is ancillary
– By Basu’s theorem T and D 2 are independent– By Basu s theorem, T and Di are independent
( Shao (2003): Mathematical Statistics, Springer)

30. One‐Sample CaseOne Sample Case
• This result is important for adaptive sample sizeThis result is important for adaptive sample size
calculations
– Stage 1 with n1= half of original sample size: changeStage 1 with n1 half of original sample size: change
second stage sample size to n2=n2(ΣDi
2)
– Conditioned on ΣD 2:– Conditioned on ΣDi :
• Test statistic T1 has exact t‐distribution with n1‐1 d.f.
• Test statistic T2 has exact t‐distribution with n2‐1 d.f. and is 2 2
independent of T1
• P‐values P1 and P2 are independent U(0,1)
• Y={n 1/2Φ‐1(P )+n 1/2Φ‐1(P )}/(n +n )1/2 is N(0 1) under H• Y={n1
1/2Φ 1(P1)+n2
1/2Φ 1(P2)}/(n1+n2)1/2 is N(0,1) under H0

31. One‐Sample CaseOne Sample Case
• Reject if Y>zReject if Y>zα
• Conditioned on ΣDi
2, type I error rate is α
• Unconditional type I error rate is α as well
• Most other two‐stage procedures are onlyMost other two stage procedures are only
approximate

32. One‐Sample CaseOne Sample Case
• Could even make other adaptations like changing p g g
primary endpoint
• Look at ΣDi
2 for each endpoint and determine
which one is primary
 2– E.g., pick endpoint with smallest Di
2
• Slight generalization of our result shows that• Slight generalization of our result shows that
conditional distribution of T given adaptation is
still exact t

33. One‐Sample CaseOne Sample Case
• Shows that conditional type I error rate givenShows that conditional type I error rate given
adaptation is controlled at level α
• Unconditional type I error rate must also be• Unconditional type I error rate must also be
controlled at level α
D i i l i i li• Derivation assumes multivariate normality
with variance/covariance not depending on
mean

34. Two‐Sample CaseTwo Sample Case
• Can use same reasoning in 2‐sample setting Ca use sa e easo g sa p e sett g
• With equal sample sizes, the numerator is
 YZYY
• Permutation distribution is distribution of
  ii
C
i
T
i YZYY
Permutation distribution is distribution of
  0,1each, iiii ZZyZ
• Let sL
2 be “lumped” variance of all data
(treatment and control)(treatment and control)

35. Two‐Sample CaseTwo Sample Case
• Mean and variance of permutation distribution p
are
  0)(EE iiii ZyyZ  
  22
)(
1
1
var Lii syy
n
yZ 






 
• Basu’s theorem shows usual 2‐sample T is
independent of sL
2 under null hypothesis ofindependent of sL under null hypothesis of
common mean
• Conditional distribution of T given sL
2 is still t

36. Two‐Sample CaseTwo Sample Case
• Two‐stage procedureTwo stage procedure
– Stage 1: look at lumped variance and change stage
2 sample size
– Conditioned on 1st stage lumped variance & H0
• T1 has t‐distribution with n1‐2 d.f.
• T2 has t‐distribution with n2‐2 d.f. & independent of T1
• P‐values P1 and P2 are independent uniforms
• {n1
1/2Φ‐1(P1)+n2
1/2Φ‐1(P2)}/(n1+n2)1/2 is N(0 1) under H0{n1 Φ (P1)+n2 Φ (P2)}/(n1+n2) is N(0,1) under H0
– Controls type I error rate conditionally and
unconditionally

37. SummarySummary
• Permutation tests are often valid even inPermutation tests are often valid even in
adaptive settings if blind is maintained
• There is a close connection between• There is a close connection between
permutation tests and t‐tests
C d d lidi f d i f• Can deduce validity of adaptive t‐tests from
validity of adaptive permutation tests