project designa.docx

1
Gear Box
StudentName: Ahmed Naseh Latif
Class: 4 Stage – Group:B
CourseTitle: Design Project
Department: Mechanic and MechatronicEngineering
College of Engineering
Salahaddin University-Erbil
Academic Year 2020-2021

2
Specifications Units value
Power to be delivered hp 16.4
Input speed rpm 1538
Output speed rpm 72
Height in 21
Width x Length in 12 x 12
Gear and bearing life Hours >11000
I/P and O/P shafts extension in 4
I/P and O/P shafts orientation In-line (reverted gearbox)
Shock level Usually low and occasional moderate shocks
Speed,Torque,andGearRatios
• Calculationof the Numberof Teethforeachgear
Usingeq.2
𝑒 =
𝜔5
𝜔2
𝑒 =
72
1538
=
1
21.36
𝑒 =
1
21.36
=
𝑁2
𝑁3
𝑁4
𝑁5
𝑁2
𝑁3
−
𝑁4
𝑁5
− √
1
21.36
−
1
4.62
` 𝑁𝑝 =
2𝑘
(1+2𝑚)sin2 𝜙
(𝑚 + √𝑚2 + (1 + 2𝑚)sin2 𝜙)
𝑁𝑝 =
2 ∗ 1
(1 + 2(4.62))sin2 20
(4.62 + √(4.62)2 + (1 + 2(4.62))sin2 20)
𝑁𝑝 = 15.637 ≈ 16 teeth
𝑁2 = 𝑁4 = 16 teeth
𝑁3 = 4.54(𝑁2) = 73.92 ≈ 73 teeth

3
𝜔5 = (
𝑁2
𝑁3
)(
𝑁4
𝑁5
)𝜔2
𝜔5 = (
16
73
) (
16
73
) ∗ 1538 = 73.88rpm
69 < 𝜔5 < 75
𝜔3 = 𝜔4 = (
16
73
) ∗ 1538 = 337 rpm
𝑇2 =
𝐻
𝜔2
𝑇2 = (
16.4ℎ𝑝
1538𝑟𝑝𝑚
) (550
𝑓𝑡 − 𝑙𝑏/𝑠
ℎ𝑝
)(
1𝑟𝑒𝑣
2𝜋𝑟𝑎𝑑
) (60
𝑠
𝑚𝑖𝑛
)
𝑇2 =
16.4 ∗ 550 ∗ 60
1750 ∗ 2𝜋
𝑇2 = 56.00𝑙𝑏𝑓.𝑓𝑡
𝑇3 = 𝑇2 (
𝜔2
𝜔3
)…… …… …. ..eq 9
𝑇3 = 56 ∗ (
1538
337
) = 255.5lbf.ft
𝑇5 = 𝑇2 (
𝜔2
𝜔5
)
𝑇5 = 56 ∗ (
1538
73.88
) = 1165.8lbf.ft
𝑃min =
(𝑁3 +
𝑁2
2
+
𝑁5
2
+ 2)
𝑌 − (clearances + wall thickness)
… …… ….. Eq.(11)
Clearances + wall thickness = 3in
𝑃min =
(76 +
16
2
+
73
2
+ 2)
22 − (3)
= 6.64 teeth /in
𝑃min = 7 teeth /in
𝑑2 = 𝑑4 =
𝑁2
𝑃
=
16
7
= 2.28in
𝑑3 = 𝑑5 =
𝑁3
𝑃
=
73
7
= 10.43in
𝑉23 =
𝜋𝑑2𝜔2
12
…… …… …. .𝐸𝑞12

4
𝑉23 =
𝜋(2.28)(1538)
12
𝑉23 = 918.0ft/min
𝑉
45 =
𝜋𝑑5𝜔5
12
𝑉
45 =
𝜋(10.43)(73.88)
12
𝑉
45 = 201.7ft/min
𝑊
23
𝑡
= 33000
𝐻
𝑉23
… …… ……… .𝐸𝑞.13
𝑊
23
𝑡
= 33000
16.4
918
= 589.5lbf
𝑊
45
𝑡
= 33000
H
𝑉
45
𝑊
45
𝑡
= 33000
16.4
201.7
= 2683.2lbf
Gear N 𝜔 T d V W
# rpm Ibf.ft in Ft//minIbf
2 16 1538 56 2.28 918 589.5
3 73 337 255.5 10.43 918 589.5
4 16 337 255.5 2.28 201.7 2683.2
5 73 73.88 1165.8 10.43 201.7 2683.2
Chapter 3
𝜎𝑐 = 𝐶𝑝√𝑊𝑡𝐾𝑜𝐾𝑣𝐾𝑠
𝐾𝑚
𝑑𝑝𝐹
𝐶𝑓
𝐼
… …… …… .Eq.(14)
𝐶𝑝 = 2300
𝐾𝑜 = 1
𝐾𝑣 = (
𝐴 + √𝑉
𝐴
)
𝐵
…… ……. Eq.15

5
𝐴 = 50 + 56(1 − 𝐵) …… …… 𝐸𝑞. (16)
𝐵 = 0.25(12 − 𝑄𝑣)2/3 … …… .. 𝐸𝑞. (17)
𝑄𝑣 = 7
𝐵 = 0.25(12 − 7)2/3 = 0.731
𝐴 = 50 + 56(1 − 0.731) = 65.1
𝐾𝑣 = (
65.1 + √201.7
65.1
)
0.731
= 1.155
𝐾𝑠 = 1 size factor
𝐾𝑚 = 𝐶𝑚𝑓 = 1 + 𝐶𝑚𝑐(𝐶𝑝𝑓𝐶𝑝𝑚 + 𝐶𝑚𝑎𝐶𝑒)…… ……. .𝐸𝑞.(18)
𝐶𝑚𝑐 = 1 because isuncrownedteeth
𝐶𝑝𝑓 = (
𝐹
10𝑑
− 0.0375 + 0.0125𝐹) … ……. .𝐸𝑞19 for 1<F<17 in.
𝐶𝑝𝑚 = 1
𝐶𝑚𝑎 = A + BF + CF^2
𝐶𝑒 = 1
𝐹 = (3 ∼ 5) (
𝜋
𝑃
) … …… ……. 𝐸𝑞. (21)
𝐹 = 4 (
𝜋
7
) = 1.8in
Roundup to F= 2 in.
𝐴 = 0.127, 𝐵 = 0.0158, 𝐶 = −0.930(10)−4
𝐶𝑚𝑎 = 0.127 + 2(0.0158) − 0.930(10)−4 ∗ (2)2
𝐶𝑚𝑎 = 0.15
𝐶𝑝𝑓 = (
2
10(2.28)
− 0.0375 + 0.0125(2)) = 0.0752
𝐶𝑓 = 1
𝐾𝑚 = 1 + 𝐶𝑚𝑐(𝐶𝑝𝑓𝐶𝑝𝑚 + 𝐶𝑚𝑎𝐶𝑒)
𝐾𝑚 = 1 + 1 ∗ (0.0752(1) + 0.15(1))
𝐾𝑚 = 1.24

6
𝐼 =
cos𝜙sin 𝜙
2𝑚𝑁
(
𝑚𝐺
𝑚𝐺 + 1
) …… ……… … Eq. (22)
𝐼 =
cos20sin 20
2(1)
(
4.62
4.62 + 1
) = 0.1321
𝐾𝑚
𝑑𝑝𝐹
𝐶𝑓
𝐼
𝜎𝑐 = 2300√2683.2 ∗ 1 ∗ 1.155 ∗ 1 ∗ (
1.24
2.28 ∗ 2
) (
1
0.1321
) = 183702psi
𝜎𝑐, all = (
𝑆𝑐
𝑆𝐻
)(
𝑍𝑁𝐶𝐻
𝐾𝑇𝐾𝑅
)… ……… .. Eq.(23)
𝐿4 = 𝑡 ∗ 𝑛4 …… …… .. Eq. (24)
𝐿4 = 11000 ∗ 60 ∗ 337 = 2.2 ∗ 108 rev
Usingfig 7 to find 𝑍𝑁
𝑍𝑁 = 0.9
𝐾𝑇 = 𝐾𝑅 = 𝐶𝐻 = 1
𝑆𝐻 = 1.2 design factor
So
𝑆𝑐 =
𝜎𝑐𝑆𝐻
𝑍𝑁
=
1.2 ∗ 183702
0.9
= 244900psi
Usingtable 3-4 the type of steel gear
𝑆𝑐 = 244900 is 𝐠𝐫𝐚𝐝𝐞 𝟑 carburized &ℎ𝑎𝑟𝑑𝑒𝑛𝑒𝑑 𝑠𝑡𝑒𝑒𝑙 𝑔𝑒𝑎𝑟,𝑡ℎ𝑒𝑟𝑒𝑓𝑜𝑟𝑒
𝜎𝑐,𝑎𝑙𝑙 = 𝑆𝑐𝑍𝑁 = 275000 ∗ 0.9 = 247500psi
𝑛𝑐 =
𝜎𝑐,𝑎𝑙𝑙
𝜎𝑐
=
247500
183702
= 1.35
Bending of gear 4
𝜎 = 𝑊𝑡𝐾𝑜𝐾𝑣𝐾𝑠
𝑃𝑑
𝐹
𝐾𝑚𝐾𝐵
𝐽
…… …… …. Eq. 26
Usingfig 8
𝑁4 = 16 teeth, then 𝐽 = 0.27

7
𝑊𝑡 = 2683.2lbf
𝐾𝑣 = 1.155
𝐾𝑜 = 1
𝐾𝑠 = 1
𝐾𝑚 = 1.24
𝐹 = 2in.
𝐾𝐵 = 1
𝑃𝑑 = 7 teeth /in
𝜎 = 2683.2 ∗ 1.155 ∗ (
7
2
) (
1.24
0.27
) = 49815psi
L=2.2 ∗ 108 rev
Thenwe use fig
𝑌𝑁 = 0.9
Usingthe same material
𝑆𝑡 = 75000
𝜎𝑎𝑙𝑙 = 𝑆𝑡𝑌𝑁 = 75000 ∗ 0.9 = 67500psi
𝑛 =
𝜎𝑎𝑙𝑙
𝜎
=
67500
49815
= 1.35
Wear of gear 5
𝐾𝑚
𝑑𝑝𝐹
𝐶𝑓
𝐼
𝜎𝑐 = 2300√2683.2 ∗ 1 ∗ 1.155 ∗ 1 ∗ (
1.24
10.43 ∗ 2
) (
1
0.1321
) = 85890psi
𝐿5 = 11000 ∗ 60 ∗ 73.88 = 4.9 ∗ 107rev
𝑍𝑁 = 1.0
Choosinggrade 2 throughhardenedsteel to250HB
Usingfig 3.6 at HB=250 to find 𝑆𝑐 = 121500psi
𝑛𝑐 =
𝜎𝑐
=
121550
85890
= 1.41
Bending of gear 5
𝑃𝑑
𝐹
𝐾𝑚𝐾𝐵
𝐽
N5=73 , thenJ=0.415

8
𝜎 = 2683.2 ∗ 1 ∗ 1.155 ∗ 1 ∗
7
2
∗
1.24
0.415
= 32410psi
Chosingthe same material grade 2
Usingfig 3.7 at HB=250
𝑆𝑖 = 41900
𝑌𝑁 = 0.97
𝜎𝑎𝑙𝑙 = 𝑆𝑡𝑌𝑁 = 41900 ∗ 0.97 = 40640
𝑛 =
𝜎𝑎𝑙𝑙
𝜎
=
40640
32410
= 1.25
Wearof gear 2
𝑉23 = 918
ft
min
𝑊
23
𝑡
= 589.5 ibf
Usingeq 15
𝐾𝑣 = (
65.1 + √918
65.1
)
0.731
= 1.32
Gear 2&3 is lowerthan4&5 therefore
Select F=1.5 in.
𝐶𝑝𝑓 = (
𝐹
10𝑑
− 0.0375 + 0.0125𝐹)
𝐶𝑝𝑓 = (
1.5
10(2.28)
− 0.0375 + 0.0125(1.5)) = 0.0470
Usingeq 20
𝐶𝑚𝑎 = 0.127 + 1.5(0.0158) − 0.930(10)−4 ∗ (1.5)2 = 0.15
𝐾𝑚 = 1 + 𝐶𝑚𝑐(𝐶𝑝𝑓𝐶𝑝𝑚 + 𝐶𝑚𝑎𝐶𝑒)
𝐾𝑚 = 1 + 1 ∗ (0.0470(1) + 0.15(1))
𝐾𝑚 = 1.21
Usingeq 14

9
𝐾𝑚
𝑑𝑝𝐹
𝐶𝑓
𝐼
𝜎𝑐 = 2300√589.5 ∗ 1 ∗ 1.32 ∗ 1 ∗ (
1.21
2.28 ∗ 1.5
)(
1
0.1321
) = 105000psi
Usingeq 24
𝐿2 = 11000 ∗ 60 ∗ 1538 = 1.0 ∗ 109rev
𝑍𝑁 = 0.8
Use table 3.4 & ant try grade 1, flame hardenedsteel
𝑆𝑐 = 170000psi
𝑛𝑐 =
𝜎𝑐
=
170000 ∗ 0.8
105000
= 1.29
Bendingof gear 2
N2=16 teeth then
J=0.27
Usingfig 3.5 as 𝐿2 = 1.0 ∗ 109rev , 𝑌𝑁 = 0.88
Usingeq 26
𝑃𝑑
𝐹
𝐾𝑚𝐾𝐵
𝐽
𝜎 = 589.5 ∗ 1 ∗ 1.32 ∗ 1 ∗
7
1.5
∗
1.21
0.27
= 16274psi
Usingthe same material fromtable 3.5 flame hardened steel
𝑆𝑡 = 45000psi
Usingeq 27
𝜎𝑎𝑙𝑙 = 𝑆𝑡𝑌𝑁 = 45000 ∗ 0.88 = 39600psi
𝑛 =
𝜎𝑎𝑙𝑙
𝜎
=
39600
16274
= 2.43

10
Wearof gear 3
𝐿3 = 11000 ∗ 60 ∗ 337 = 2.2 ∗ 108rev
𝑍𝑁 = 0.9
𝐾𝑚
𝑑𝑝𝐹
𝐶𝑓
𝐼
𝜎𝑐 = 2300√589.5 ∗ 1 ∗ 1.32 ∗ 1 ∗ (
1.21
10.43 ∗ 1.5
) (
1
0.1321
) = 49092psi
Chosinggrade 1 through hardenedsteelto200HB
Usingfig 3.6 then
𝑆𝐶 = 90000psi
𝑛𝑐 =
𝜎𝑐
=
90000 ∗ 0.9
49092
= 1.65
Bendingof gear 3
N3=73 then J=0.415 from fig3.4
𝑃𝑑
𝐹
𝐾𝑚𝐾𝐵
𝐽
𝜎 = 589.5 ∗ 1 ∗ 1.32 ∗ 1 ∗
7
1.5
∗
1.21
0.415
= 10590psi
Fig3.5
𝑌𝑁 = 0.9
Usingthe same material grade 1
𝑆𝐶 = 28000psi
𝑛 =
𝜎𝑎𝑙𝑙
𝜎
=
28000 ∗ 0.9
10590
= 2.38

11
Gear Material Treatment Wear stress Bendingstress d F
Grade psi psi in in
2 1 Flame-hardened 170000 45000 2.28 1.5
3 1 Through-hardenedto200HB 90000 28000 10.43 1.5
4 3 Carburizedandhardened 275000 75000 2.28 2.0
5 2 Through-hardenedto250HB 121550 41900 10.43 2.0
Chapter 4
𝐹2=𝐹3=1.5 in.
𝐹
4=𝐹5=2.0 in.
𝑊
23
𝑡
= 589.5lbf
𝑊
45
𝑡
= −2683.2lbf
𝑊𝑟 = 𝑊𝑡tan𝜙 …… …… …… .. 𝐸𝑞.28
𝑊
23
𝑟
= 𝑊
23
𝑡
tan 𝜙
𝑊
23
𝑟
= 589.5tan 20
𝑊
23
𝑟
= −215lb𝑓
𝑊
45
𝑟
= −977lbf
Determinationof reactionforces on bearings

12
x-zplane:
∑𝑀𝐴 = 0
𝑊
23
𝑡
∗ 𝑥1 − 𝑊
45
𝑡
∗ 𝑥2 + 𝑅𝐵𝑍 ∗ 𝑥3 = 0
589.5(2.75 − 0.75) − 2683.2(8.5 − 0.75)
+𝑅𝐵𝑍(10.75 − 0.75) = 0
𝑅𝐵𝑍 = 1962 lbf
∑𝐹
𝑧 = 0
𝑅𝐴𝑍 + 𝑊
23
𝑡
− 𝑊
45
𝑡
+ 𝑅𝐵𝑍 = 0
𝑅𝐴𝑍 = −589.5 + 2683.2 − 1962
𝑅𝐴𝑍 = 132 lb𝑓
x-yplane :
∑𝑀𝐴 = 0
𝑊
23
𝑟
∗ 𝑥1 + 𝑊
45
𝑟
∗ 𝑥2 − 𝑅𝐵𝑌 ∗ 𝑥3 = 0
215(2.75 − 0.75) + 977(8.5 − 0.75)
−𝑅𝐵𝑌(10.75− 0.75) = 0
𝑅𝐵𝑌 = 800 lbf
∑𝐹𝑌 = 0
𝑅𝐴𝑌 − 𝑊
23
𝑟
− 𝑊
45
𝑟
+ 𝑅𝐵𝑌 = 0
𝑅𝐴𝑌 = 215 + 977 − 800
𝑅𝐴𝑌 = 392 lbf
Torque diagram:
𝑇3 = 𝑊
23
𝑡
∗
𝑑3
2
𝑇3 = 589.5 ∗
10.43
2
𝑇3 = 3074 lbf. in
𝑇4 = −W45
t
∗
d4
2
𝑇4 = −2683.2 ∗
2.28
2
𝑇4 = −3060lbf.in
The shear force & bearingmoment diagram
x-yplane :

13
𝑉
𝐴𝐺 = 𝑅𝐴𝑌 = 392 lbf
𝑉𝐺𝐽 = 𝑅𝐴𝑌 − 𝑊
23
𝑟
𝑉𝐺𝐽 = 392 − 215
𝑉𝐺𝐽 = 177 lbf
𝑉
𝐽𝐵 = 𝑉𝐺𝐽 − 𝑊
45
𝑟
𝑉
𝐽𝐵 = 177 − 977
𝑉
𝐽𝐵 = −800 = 𝑅𝐵𝑌 𝑀𝐺 = 𝑅𝐴𝑌 ∗ X1 = 784 Ibf.in
𝑀𝐽 = 𝑅𝐴𝑌(8.5 − 0.75) − 𝑊
23
𝑟
(8.5 − 2.75)
𝑀𝐽 = 392 ∗ (8.5 − 0.75) − 215(8.5 − 2.75)
𝑀𝐽 = 1800 Ibf. in
𝑀𝐵 = 𝑅𝐴𝑌(10.75 − 0.75) − 𝑊
23
𝑟
(10.75 − 2.75) − 𝑊
45
𝑟
(10.75 − 8.5)
𝑀𝐵 = 392(10) − 215(8) − 977(2.25)
𝑀𝐵 = 1.75 ≈ 0
x-zplane:
𝑉
𝐴𝐺 = 𝑅𝐴𝑍 = 132lbf
𝑉𝐺𝐽 = 𝑅𝐴𝑍 + 𝑊
23
𝑡
𝑉𝐺𝐽 = 132 + 589.5
𝑉𝐺𝐽 = 722lbf
𝑉
𝐽𝐵 = 𝑉𝐺𝐽 − 𝑊
45
𝑡
𝑉
𝐽𝐵 = 722 − 2683.2
𝑉
𝐽𝐵 = −1962 = 𝑅𝐵𝑍
𝑀𝐺 = 𝑅𝐴𝑍 ∗ 𝑥1
𝑀𝐺 = 132 ∗ 2
𝑀𝐺 = 264 lbf.in
𝑀𝐽 = 𝑅𝐴𝑍(8.5 − 0.75) + 𝑊
23
𝑡
(8.5 − 2.75)
𝑀𝐽 = 132 ∗ (8.5 − 0.75) + 589.5(8.5 − 2.75)
𝑀𝑗 = 4412.6 lbf.in
𝑀𝐵 = 𝑅𝐴𝑍(10.75 − 0.75) + 𝑊
23
𝑡
(10.75 − 2.75) − 𝑊
45
𝑡
(10.75 − 8.5)
𝑀𝐵 = 132(10) + 589.5(8) − 2683.2(2.25)
𝑀𝐵 = −1.2 ≈ 0
The total bendingmomentdiagram
𝑀𝐺 = √(784)2 + (264)2
𝑀𝐺 = 827 lbf. in
𝑀𝐽 = √(1800)2 + (4412.6)2
𝑀𝐽 = 4766 lbf.in

14
The shoulderatpointI:
𝑀𝐼 = 𝑅𝐴𝑌(7.5 − 0.75) − 𝑊
23
𝑟
(7.5 − 2.75)
𝑀𝐼 = 392 ∗ (7.5 − 0.75) − 215(7.5 − 2.75)
𝑀𝐼 = 1625 Ibf.in x − y plane
𝑀𝐼 = 𝑅𝐴𝑍(7.5− 0.75) + 𝑊
23
𝑡
(7.5 − 2.75)
𝑀𝐼 = 132 ∗ (7.5 − 0.75) + 589.5(7.5 − 2.75)
𝑀𝐼 = 3691.1 lbf.in x − z plane
𝑀𝐼 = √(1625)2 + (3691.1)2
𝑀𝐼 = 4033 lbf.in
The midrange torque is:
𝑇𝑀 = 3067 Ibf.in
𝑀𝑀 = 𝑇𝑎 = 0
Extimation ofthe stress concentrations:
D/d=1.2~1.5
r/d=0.02~0.06
the MARIN equation:
𝑆𝑒 = 𝑘𝑎𝑘𝑏𝑘𝑐𝑘𝑑𝑘𝑒𝑘𝑓𝑆𝑒
′ … …… …… ..𝐸𝑞.29
𝑘𝑎 = 𝑎𝑆𝑢𝑡
𝑏
⋯⋯⋯⋯⋯⋯𝐸𝑞 ⋅ 30
A 1018CD steel ischosen:
𝑆𝑢𝑡=64 kpsi
𝑆𝑦 = 54 kpsi
Therefore
𝑎 = 2.7kpsi 𝑏 = −0.265
𝑘𝑎 = 2.7(64)−0.265 = 0.897
𝑘𝑏 = 0.9
𝑘𝑐 = 𝑘𝑑 = 𝑘𝑒 = 1

15
𝑆𝑒
′ = 0.5 ∗ 𝑆𝑢𝑡 for 𝑆𝑢𝑡 ≤ 200kpsi
𝑆𝑒
′ = 100kpsi for 𝑆𝑢𝑡 > 200𝑘𝑝𝑠𝑖
𝑆𝑒 = 0.897 ∗ 0.9 ∗ 0.5 ∗ 64 eq.29
𝑆𝑒 = 25.8 kpsi
Assuming shoulder-fillet well-rounded r/d=0.1 then:
From table 4-3
𝐾𝑡 = 1.7 and
𝐾𝑡𝑠 = 1.5
𝐾𝑓 = 𝐾𝑡 and 𝐾𝑓𝑠 = 𝐾𝑡𝑠
𝑀𝑚 = 𝑇𝑎 = 0
𝑑 = √
16𝑛
𝜋
{
2𝐾𝑓𝑀𝑎
𝑆𝑒
+
𝐾𝑓𝑠𝑇𝑚
𝑆𝑢𝑡
√3}
3
… …… …… .. 𝐸𝑞. 32
𝑑 = √
16 ∗ 1.5
𝜋
{
2 ∗ 1.7 ∗ 4033
25800
+
1.5 ∗ 3067
64000
√3}
3
𝑑 = 1.71in
From the standards:
d= 1
11
16
= 1.6875 in.
D/d=1.2
D=1.6875*1.2=2.025 in.
D= 2 in.
D/d=
2
1.6875
= 1.185
Assume
r/d=0.1
r=0.1*1.6875=0.16 in.
using fig 4.5 for r/d=0.1 & D/d=1.185
𝐾𝑡 = 1.6
Using fig 4.6 for find q
q=0.82

16
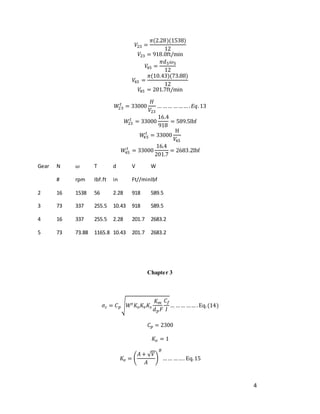
𝐾𝑓 = 1 + 𝑞(𝐾𝑡 − 1)… …… …𝐸𝑞.33
𝐾𝑓 = 1 + 0.82(1.6 − 1)
𝐾𝑓 = 1.49
Using fig 4.7 r/d=0.1 & D/d=1.185
𝐾𝑡𝑠 = 1.35
Using fig4.8 for r=1.6 in
q=0.95
𝐾𝑓𝑠 = 1 + 𝑞shear(𝐾𝑡𝑠 − 1) ……… …𝐸𝑞.34
𝐾𝑓𝑠 = 1 + 0.95(1.35 − 1)
𝐾𝑓𝑠 = 1.33
𝐾𝑎 = 0.897 (not changed)
𝑘𝑏 = (
𝑑
0.3
)
−0.107
for 0.11 ≤ 𝑑 ≤ 2.0 in. …… …. Eq.35
𝑘𝑏 = 0.91𝑑−0.157 for 2.0 < 𝑑 ≤ 10 in. ……… .. 𝐸𝑞. 36
𝑘𝑏 = (
1.6875
0.3
)
−0.107
= 0.831
𝑆𝑒 = 0.897 ∗ 0.831 ∗ 0.5 ∗ 64
𝜎𝑎
′ =
32𝐾𝑓𝑀𝑎
𝜋𝑑3
𝜎𝑎
′ =
32 ∗ 1.49 ∗ 4033
𝜋(1.6875)3
𝜎𝑎
′ = 12737 psi
𝜎𝑚
′ = (𝜎𝑚
2 + 3𝜏𝑚
2 )1/2 = [(
32𝐾𝑓𝑀𝑚
𝜋𝑑3
)
2
+ 3 (
16𝐾𝑓𝑠𝑇𝑚
𝜋𝑑3
)
2
]
1/2
𝜎𝑚
′ = [3(
𝜋𝑑3
)
2
]
1/2
𝜎𝑚
′ =
√3 ∗ 16 ∗ 1.33 ∗ 3067
𝜋(1.6875)3
𝜎𝑚
′ = 7488 psi
1
𝑛𝑓
=
𝜎𝑎
′
𝑆𝑒
+
𝜎𝑚
′
𝑆𝑢𝑡
1
𝑛𝑓
=
12737
23700
+
7488
64000
= 0.654
𝑛𝑓 = 1.53

17
Check for yielding:
𝑛𝑦 =
𝑆𝑦
𝜎max
′
𝑛𝑦 =
54000
(12737 + 7488)
= 2.66
The keyway
M=4030 Ibf.in
Assume
r/d=0.02
r=0.02*1.6875
r=0.033 in.
using fig 4.5
𝐾𝑡 = 2.4
Using fig 4.6
q=0.66
using eq.33
𝐾𝑓 = 1 + 𝑞(𝐾𝑡 − 1)… …… …𝐸𝑞.33
𝐾𝑓 = 1 + 0.66(2.4 − 1)
𝐾𝑓 = 1.92
Using fig 4.7
𝐾𝑡𝑠 = 2.2
Fig 4.8 gives
𝑞𝑠 = 0.91
Using eq.34

18
𝐾𝑓𝑠 = 1 + 𝑞shear(𝐾𝑡𝑠 − 1) ……… …𝐸𝑞.34
𝐾𝑓𝑠 = 1 + 0.91(2.2 − 1)
𝐾𝑓𝑠 = 2.09
𝜎𝑎
′ =
32𝐾𝑓𝑀𝑎
𝜋𝑑3
𝜎𝑎
′ =
32 ∗ 1.92 ∗ 4030
𝜋(1.6875)3
𝜎𝑎
′ = 16400 psi
𝜎𝑚
′ = [3(
𝜋𝑑3
)
2
]
1/2
𝜎𝑚
′ =
√3 ∗ 16 ∗ 2.09 ∗ 3067
𝜋(1.6875)3
𝜎𝑚
′ = 11767 psi
1
𝑛𝑓
=
𝜎𝑎
′
𝑆𝑒
+
𝜎𝑚
′
𝑆𝑢𝑡
1
𝑛𝑓
=
16400
23700
+
11767
64000
= 0.876
𝑛𝑓 = 1.14
Is not good
Trying steel 1050CD with 𝑆𝑢𝑡 = 100 kpsi & 𝑆𝑦 = 84 kpsi
Using eq 30
𝑘𝑎 = 𝑎𝑆𝑢𝑡
𝑏
⋯⋯⋯⋯⋯⋯𝐸𝑞 ⋅ 30
𝑘𝑎 = 2.7(100)−0.265
𝑘𝑎 = 0.797
Using eq.29
𝑆𝑒 = 0.797 ∗ 0.831 ∗ 0.5 ∗ 100 eq. 29
Fig 4.6 gives
q=0.73

19
𝐾𝑓 = 1 + 𝑞(𝐾𝑡 − 1)… …… …𝐸𝑞.33
𝐾𝑓 = 1 + 0.73(2.4 − 1)
𝐾𝑓 = 2.02
𝜎𝑎
′ =
32 ∗ 2.02 ∗ 4030
𝜋(1.6875)3
𝜎𝑎
′ = 17255 psi
1
𝑛𝑓
=
𝜎𝑎
′
𝑆𝑒
+
𝜎𝑚
′
𝑆𝑢𝑡
1
𝑛𝑓
=
17255
33100
+
11767
100000
= 0.64
𝑛𝑓 = 1.56
Inspecting at point K
𝑀𝑎 = 2650 Ibf.in
𝑀𝑚 = 𝑇𝑎 = 𝑇𝑚 = 0
Using table 4.3
𝐾𝑡 = 𝐾𝑓 = 5.0
𝜎𝑎 =
32𝐾𝑓𝑀𝑎
𝜋𝑑3
𝜎𝑎 =
32 ∗ 5 ∗ 2650
𝜋(1.6875)3
𝜎𝑎 = 28086psi
𝑛𝑓 =
𝑆𝑒
𝜎𝑎
𝑛𝑓 =
33100
28086
= 1.17
Is not good
Using the shaft diameter of 1.6875 in. to gets:
a=0.068 in.
t=0.048 in.
r=0.01 in.

20
𝑟
𝑡
= 0.208
𝑎
𝑡
= 1.42
𝑑 = 𝐷 − 2𝑡
𝑑 = 1.6875 − 2 ∗ 0.048
𝑑 = 1.5915 in
Using fig 4.9
q=0.65
𝐾𝑡 = 4.3
𝐾𝑓 = 1 + 𝑞(𝐾𝑡 − 1)… …… …𝐸𝑞.33
𝐾𝑓 = 1 + 0.65(4.3 − 1)
𝐾𝑓 = 3.15
𝜎𝑎 =
32𝐾𝑓𝑀𝑎
𝜋𝑑3
𝜎𝑎 =
32 ∗ 3.15 ∗ 2650
𝜋(1.6875)3
𝜎𝑎 = 17694 psi
𝑛𝑓 =
𝑆𝑒
𝜎𝑎
𝑛𝑓 =
33100
17694
= 1.87
Determination of 𝐷6
D/d = 1.2~1.5
d = D/1.2
d = 1.6875/1.2 = 1.406 in.
𝐷6 = 1.4 in.
Inspecting point M
x-y plane
𝑀𝑀 = 𝑅𝐴𝑌(10.25 − 0.75) − 𝑊
23
𝑟
(10.25 − 2.75) − 𝑊
45
𝑟
(10.25 − 8.5)
𝑀𝑀 = 392 ∗ (10.25 − 0.75) − 215(10.25 − 2.75) − 977(10.25 − 8.5)
𝑀𝑀 = 401.75 lbf.𝑖𝑛
x-z plane

21
𝑀𝑀 = 𝑅𝐴𝑍(10.25 − 0.75) + 𝑊
23
𝑡
(10.25 − 2.75) − 𝑊
45
𝑡
(10.25 − 8.5)
𝑀𝑀 = 132 ∗ (10.25 − 0.75) + 589.5(10.25 − 2.75) − 2683.2(10.25 − 8.5)
𝑀𝑀 = 979.65 lbf.in
𝑀𝑀 = √(401.75)2 + (979.65)2
𝑀𝑀 = 1058.82 lbf.in
𝑀𝑎 = 1058.82 lbf.in
𝑀𝑚 = 𝑇𝑚 = 𝑇𝑎 = 0
Using table 4.3
r/d = 0.05
𝐾𝑓 = 1.9
d = 1 in.
r = 0.05*1 = 0.05 in.
using fig 4.6
𝑞 = 0.75
𝐾𝑓 = 1 + 𝑞(𝐾𝑡 − 1)
𝐾𝑓 = 1 + 0.75(1.9 − 1)
𝐾𝑓 = 1.675
𝜎𝑎 =
32𝐾𝑓𝑀𝑎
𝜋𝑑3
𝜎𝑎 =
32 ∗ 1.675 ∗ 1058.82
𝜋(1)3
𝜎𝑎 = 18050 psi
𝑛𝑓 =
𝑆𝑒
𝜎𝑎
𝑛𝑓 =
33100
18050
= 1.83
𝐷1 = 𝐷7 = 1 in.
𝐷2 = 𝐷6 = 1.4 in.
𝐷3 = 𝐷5 = 1.6875 in.
𝐷4 = 2 in.
The rigidity of the shaft
Deflection of the shaft

22
𝐼 =
𝜋𝑑4
64
𝐼𝐷𝐻 = 𝐼𝐼𝑀 =
𝜋(1.6875)4
64
= 0.398 in4
𝐼𝐻𝐼 =
𝜋(2.0)4
64
= 0.785in4
x-z plane
Shoulder H
(
𝑀𝐺
𝐼𝐴𝐻
)
𝐺
=
264
0.398
= 663 lbf/in3
𝑀𝐻 = 𝑅𝐴𝑍(3.5− 0.75) + 𝑊
23
𝑡
(3.5 − 2.75)
𝑀𝐻 = 132(3.5 − 0.75) + 589.5(3.5 − 2.75)
𝑀𝐻 = 805.125 lbf.in
(
𝑀𝐻
𝐼𝐴𝐻
)
𝐻
=
805.125
0.398
= 2023 lbf/in3
slope𝐺𝐻 =
2023 − 663
0.75
= 1813lbf/in4
(
𝑀𝐻
𝐼𝐻𝐼
)
𝐻
=
805.125
0.785
= 1026 lbf/in3
(
𝑀𝐼
𝐼𝐻𝐼
)
𝐼
=
4033
0.785
= 5138 lbf/in3
slope 𝐻𝐼 =
5138 − 1026
4
= 1027.8 lbf/in4
Δ𝑚 = slope𝐺𝐻 − slope 𝐻𝐼
Δ𝑚 = 1027.8 − 1813 = −785.1 lbf/in4
step𝐻 = (
𝑀𝐻
𝐼𝐻𝐼
)
𝐻
− (
𝑀𝐻
𝐼𝐴𝐻
)
𝐻
step𝐻 = 1026 − 2023 = −997 lbf/in3
Shoulder I:
(
𝑀𝐼
𝐼𝐼𝐵
)
𝐼
=
4033
0.398
= 10133 lbf/in3
(
𝑀𝐽
𝐼𝐼𝐵
)
𝐽
=
4766
0.398
= 11975 lbf/in3
slope𝐼𝐽 =
11975 − 10133
1
= 1842lbf/in4

23
Δ𝑚 = slop𝑒𝐼𝐽 − slope𝐻𝐼
Δ𝑚 = 1842 − 1027.8 = 814.2 lbf/in4
step𝐼 = (
𝑀𝐼
𝐼𝐼𝐵
)
𝐼
− (
𝑀𝐼
𝐼𝐻
)
1
step𝐼 = 10133 − 5138 = 4995 lbf/in3
Chapter 5
Bearings
Bearing selection:
Gear & bearing life =11000 hours
Counter shaft speed = 337 rpm
Estimated bore size= 1 in.
Estimated bearing width= 1 in.
Reliability= 99%
Left bearing reactions
𝑅𝐴𝑍 = 132 Ibf, 𝑅𝐴𝑦 = 392 Ibf, 𝑅𝐴 = 414 Ibf
Right bearing reactions
𝑅𝐵𝑍 = 1962 Ibf, 𝑅𝐵𝑦 = 800 Ibf, 𝑅𝐵 = 2119 Ibf
Right bearing selection procedure
𝑥𝐷 =
𝐿
𝐿10
=
60𝐿𝐷𝑛𝐷
60𝐿𝑅𝑛𝑅
𝑥𝐷 =
60 ∗ 11000 ∗ 337
106
𝑥𝐷 =
2.8 ∗ 108
106
= 222

24
Assuming a ball bearing with
a=3
using eq 5.2
𝐶10 = 𝑎𝑓𝐹𝐷 [
𝑥𝐷
𝑥𝑜 + (𝜃 − 𝑥0)(1− 𝑅𝐷)
1
𝑏
]
1
𝑎
𝑎𝑓 = 1 for steady loads.
𝐶10 = 2119 ∗ [
222
0.02 + 4.439(1 − 0.99)
1
1.483
]
1
3
𝐶10 = 21289lbf
𝐶10 = 21289lbf∗ 0.00444
𝐶10 = 94.5 kN
Is very high
Choosing roller bearing
a=10/3
𝐶10 = 2119 ∗ [
222
0.02 + 4.439(1− 0.99)
1
1.483
]
3
10
𝐶10 = 16900
𝐶10 = 16900 ∗ 0.00444
𝐶10 = 75.0 kN
Checking this load with SKF bearing catalogue for 1 in.
𝐶 = 83kN
𝐶 = 18568lbf
𝐼𝐷 = 30mm = 1.188in
𝑂𝐷 = 72mm = 2.834in.
𝑊 = 27mm = 1.063in.
Shoulder diameter = 36.8mm = 1.45in.
Maximum fillet radius = 1.09mm = 0.043in.

25
Left bearing selection procedure
Choosing a=3
Using eq 5.2
𝐶10 = 414 ∗ [
222
0.02 + 4.439(1− 0.99)
1
1.483
]
1
3
𝐶10 = 4159 ∗ 0.00444
𝐶10 = 18.47 kN
The left bearing selection specifications
𝐼𝐷 = 25mm = 1.0in
𝑂𝐷 = 62mm ≈ 2.5in
𝑊 = 17mm = 0.67in
𝐶 = 23.4kN = 5270lbf
Shoulder diameter = 1.3~1.4 in.
Maximum fillet radius = 0.08 in.
Chpter six
Key&keyway design
From the previous data:
Bore in. Hub length in. Torque Ibf.in. Safety factor
Gear 3 1.6875 1.5 3067 2
Gear 4 1.6875 2.0 3067 2

26
Using table 6.3 for asquare key
Shaft diameter w h Keyway design
1.6875…….1 11/16 3/8 3/8 3/16
Choosing key material of 1020 CD steel
With 𝑆𝑦 = 57 kpsi
𝐹 =
𝑇
𝑟
𝐹 =
3067 ∗ 2
1.6875
= 3635 lbf
𝑎 =
ℎ
2
∗ 𝑙
𝑎 =
3/8
2
∗ 𝑙 = 0.1875𝑙
𝜎 =
𝐹
𝑎
=
3635
0.1875𝑙
But
𝑛 =
𝑆𝑦
𝜎
𝜎 =
𝑆𝑦
𝑛
𝑆𝑦
𝑛
=
3635
0.1875𝑙
𝑙 =
3635 ∗ 𝑛
0.1875 ∗ 𝑆𝑦
𝑙 =
3635 ∗ 2
0.1875 ∗ 57000
𝑙 = 0.68 in.
Chpater seven
𝑙 =
1
2
+
1
2
= 1.0 𝑖𝑛

27
𝑡 =
41
64
𝑖𝑛
2
(12 )
𝐿 = 𝑙 + 𝑡 + 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 2 𝑡ℎ𝑟𝑒𝑎𝑑𝑠
𝐿 = 1.0 +
41
64
+
2
12
= 1.81 𝑖𝑛
Round up to the next standard size
L=1.81 in
𝐿𝑇 = 2𝑑 +
1
4
𝑖𝑛.
The length of the threaded part is
𝐿𝑇 = 2 ∗ 0.5625 + 0.25 = 1.375 𝑖𝑛
𝑙𝑑 = 𝐿 − 𝐿𝑇
𝑙𝑑 = 1.81 − 1.375 = 0.435 𝑖𝑛
𝑙𝑡 = 𝑙 − 𝑙𝑑 = 1.0 − 0.435 = 0.565 𝑖𝑛.
Using fig.(4.7)
𝐴𝑡 = 0.182 𝑖𝑛2
𝐴𝑑 = 𝜋
0.56252
4
= 0.248 𝑖𝑛2
𝐾𝑏 =
𝐴𝑡𝐴𝑑𝐸
𝐴𝑑𝑙𝑡+𝐴𝑡𝑙𝑑
𝐾𝑏 =
0.182 ∗ 0.248 ∗ 30
0.248 ∗ 0.565 + 0.182 ∗ 0.435
= 6.39 𝑀𝑙𝑏𝑓/𝑖𝑛
𝐾𝑚 =
0.5774𝜋𝐸𝑑
2𝑙𝑛(5
0.5774𝑙 + 0.5𝑑
0.5774𝑙 + 2.5𝑑
)

28
𝐾𝑚 =
0.5774 ∗ 𝜋 ∗ 14 ∗ 0.5625
2𝑙𝑛(5
0.5774 ∗ 1.0 + 0.5 ∗ 0.5625
0.5774 ∗ 1.0 + 2.5 ∗ 0.5625
)
= 9.25 𝑀𝑙𝑏𝑓/𝑖𝑛
Using table 7.5 to find 𝐾𝑚
𝐾𝑚 = 𝐸𝑑𝐴 ∗ 𝑒
𝐵
𝐴
𝑙
𝐾𝑚 = 14 ∗ 0.5625 ∗ 0.778 ∗ 𝑒
0.616
0.625
1.5
𝐾𝑚 = 8.96 𝑀 𝑙𝑏𝑓/in
𝑒𝑟𝑟𝑜𝑟 =
9.25 − 8.96
9.25
≈ 3.1%
The joint stiffness
𝐶 =
𝐾𝑏
𝐾𝑏 + 𝐾𝑚
𝐶 =
6.39
6.39 + 9.25
= 0.408
Using table 7.6 to obtain the minimum proof strength of grade 5 SAE bolt
𝐹𝑖 = 0.75 ∗ 0.182 ∗ 85 = 11.6 𝑘𝑙𝑏𝑓
𝑛 =
𝑆𝑝𝐴𝑡 − 𝐹𝑖
𝐶(
𝑃
𝑛
)
Rearrangement gives
𝑁 =
𝐶𝑛𝑃
𝑆𝑝𝐴𝑡 − 𝐹𝑖
𝑁 =
0.408 ∗ 2 ∗ 25
85 ∗ 0.182 − 11.6
= 5.27
Roundup to 6 bolts and check for n

29
𝑛 =
85 ∗ 0.182 − 11.6
0.408 ∗
25
6
= 2.27
The value of n is higher than the required value (2)
The tightening torque is
𝑇 = 𝐾𝐹𝑖𝑑
𝑇 = 0.2 ∗ 11600 ∗ 0.5625 = 1305 𝐼𝑏𝑓/𝑖𝑛

project designa.docx

More Related Content

Similar to project designa.docx

More from Mahamad Jawhar

Recently uploaded

project designa.docx