1. PRML 読書会第 14 回 10.7 2010/5/8 twitter:ruto5

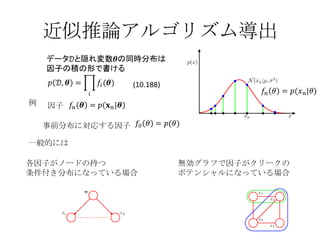
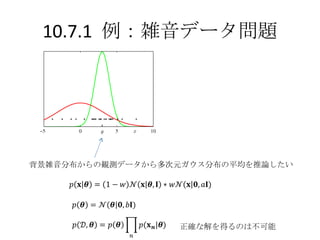
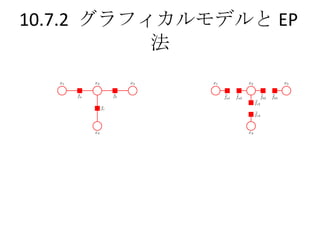
2. 目次 10.7 EP 法・・・決定性の近似推論法 , ガウス分布による近似の方法の１つ アルゴリズムの導出と説明、変分ベイズ法との違い 10.7.1 雑音データ問題・・・観測データと雑音データの混合ガウス分布から平均を推定 10.7.2 グラフィカルモデルと EP 法・・・因子グラフを使って分解し EP 法を適用する １０章：解析的な近似 ロジスティック回帰モデルは、正確な積分ができないので何らかの近似を導入する 11 章：数値的な近似

3. KL ダイバージェンス最小化 (10.185) (10.186) モーメント一致法：ガウス分布の平均と分散にあわせて近似する手法 (10.187)

4. 近似推論アルゴリズム導出 各因子がノードの持つ 条件付き分布になっている場合 無効グラフで因子がクリークの ポテンシャルになっている場合 例 因子 事前分布に対応する因子 一般的には (10.188)

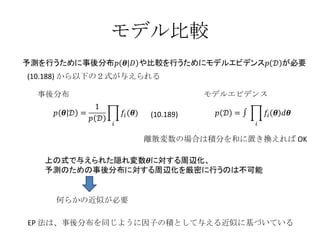
5. モデル比較 事後分布 モデルエビデンス 何らかの近似が必要 (10.188) から以下の２式が与えられる 離散変数の場合は積分を和に置き換えれば OK EP 法は、事後分布を同じように因子の積として与える近似に基づいている (10.189)

6. 因子の積として与える近似 近似式 この式は真の事後分布に関する平均操作を含むため、最小化は不可能 因子を指数型分布と仮定した場合、因子の積も指数型分布になり 有限個の十分統計量を使って表すことができる 真の事後分布と近似分布の KL ダイバージェンスを最小化して求めたい

7. 近似精度 利点：簡単に解ける アルゴリズムが繰り返しを使わない←モンテカルロ法みたいなイメージ 欠点：各因子が独立に近似されるため、それらの積は近似精度落ちる EP 法なら 各因子の最適化を、他の因子による近似すべてを条件として順番に行って 最適化するので、近似精度悪くならないのでは？ 最初に各因子を初期化した後、各因子を巡回して、１つずつ近似を改良していく 十分統計量はパラメータを持たなくて良い

8. 改良した因子の決め方 概念 この方法は、近似が残りの因子によって定まる高い確率の領域で、最も正確に なることを保証している この効果の例は「雑音データ問題」に適用する時に説明 (10.7.1) (10.193)

9. KL 最小化 を最小化することで求められる 指数型分布族だから簡単に解ける (10.196) (10.195) (10.197)

10. 改良後の近似分布パラメータ 一般的には どんな指数型分布族の分布についても、正規化さえできれば必要な期待値は 簡単に得られる

11. EP 法による近似の例 赤：ラプラス近似 緑：変分近似 青： EP 法

12. K の導出 この式の導出に (10.195) を使用した K の値はゼロ次のモーメントを一致させることで以下の式が得られる

13. 実際の推定

14. EP 法アルゴリズム まとめ 同時分布 近似事後分布

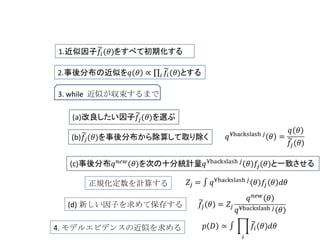
15. 3. while 近似が収束するまで 正規化定数を計算する (d) 新しい因子を求めて保存する 4. モデルエビデンスの近似を求める

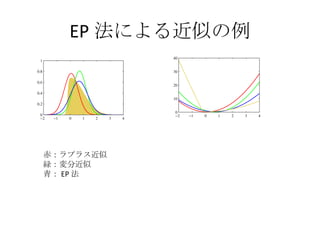
16. EP 法の長所と短所 ※ ロジスティックモデルは単峰型の代表として扱われているとのこと Kuss and Rasmussen,2006 の論文に MCMC でサンプリングした結果に 近いことが書かれているとのこと

17. 10.7.1 例：雑音データ問題 背景雑音分布からの観測データから多次元ガウス分布の平均を推論したい 正確な解を得るのは不可能

18. 特定の因子近似例 改良

19. 性能比較 真の値からみた関係 モデルエビデンスからみ見た関係 事後分布から予測された平均値に対する誤差と浮動小数点演算数（ FLOPS) -> FLOPS と誤差の関係図は、論文でよく見かけるらしい

20. 10.7.2 グラフィカルモデルと EP 法