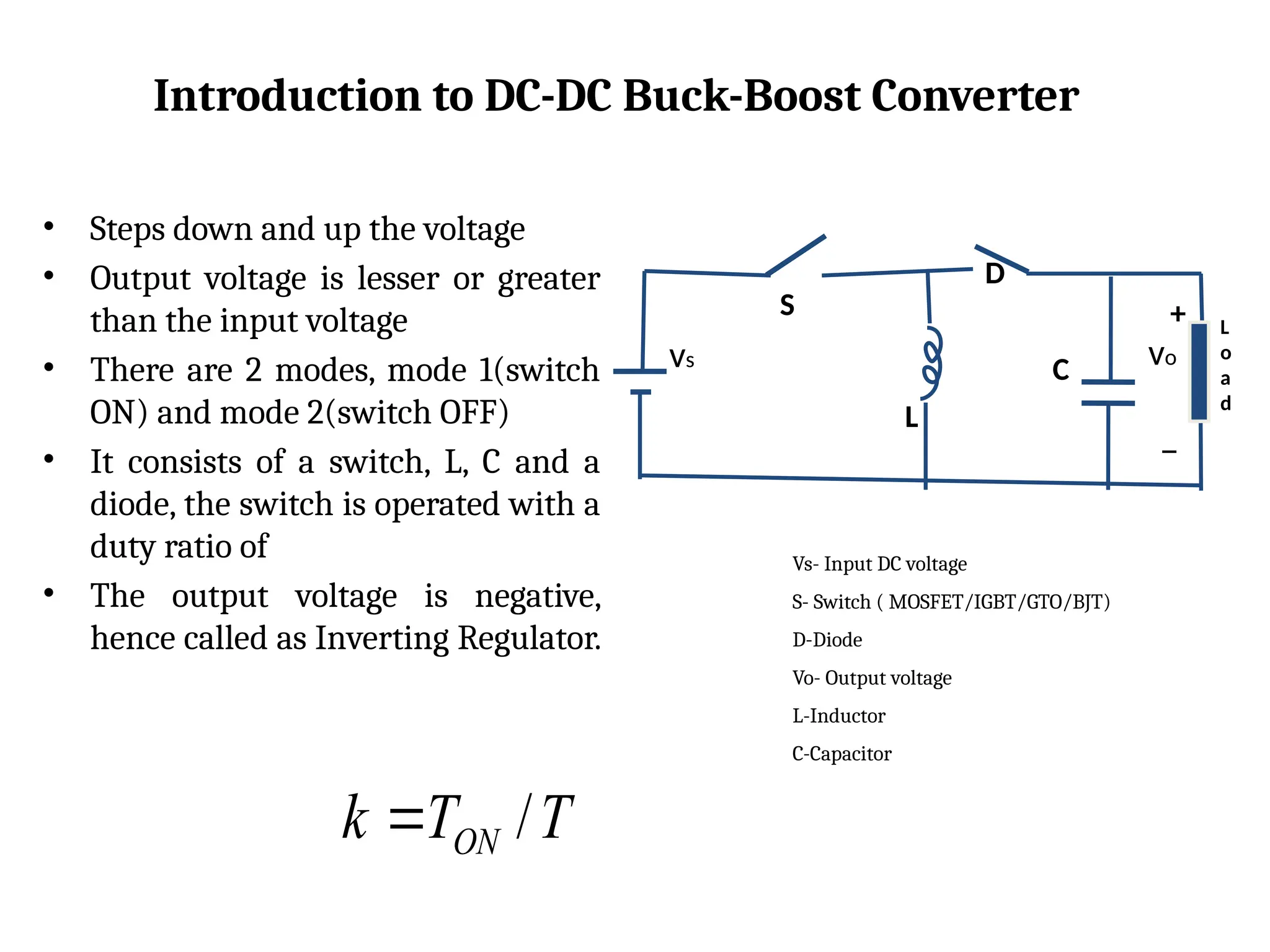
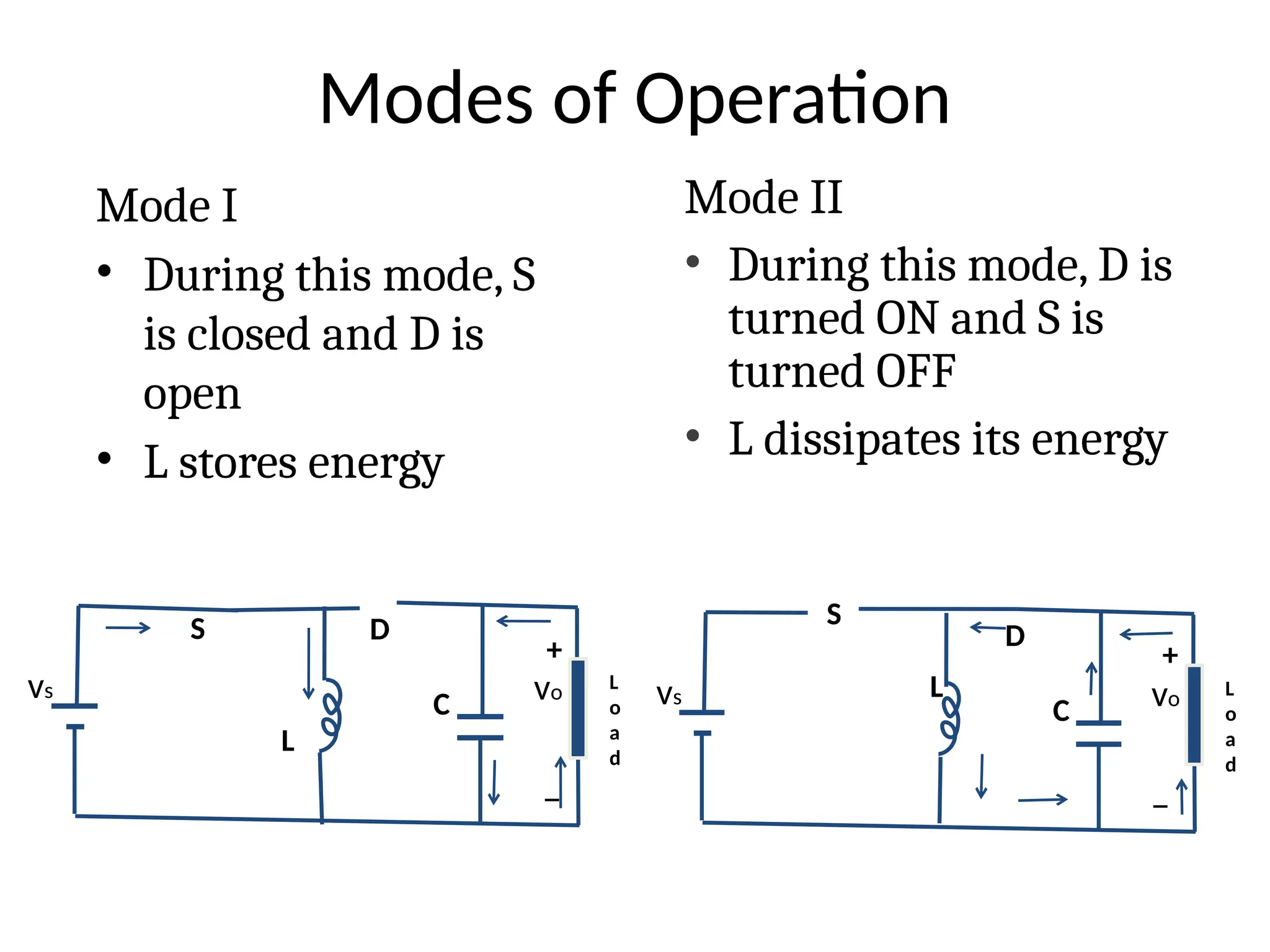
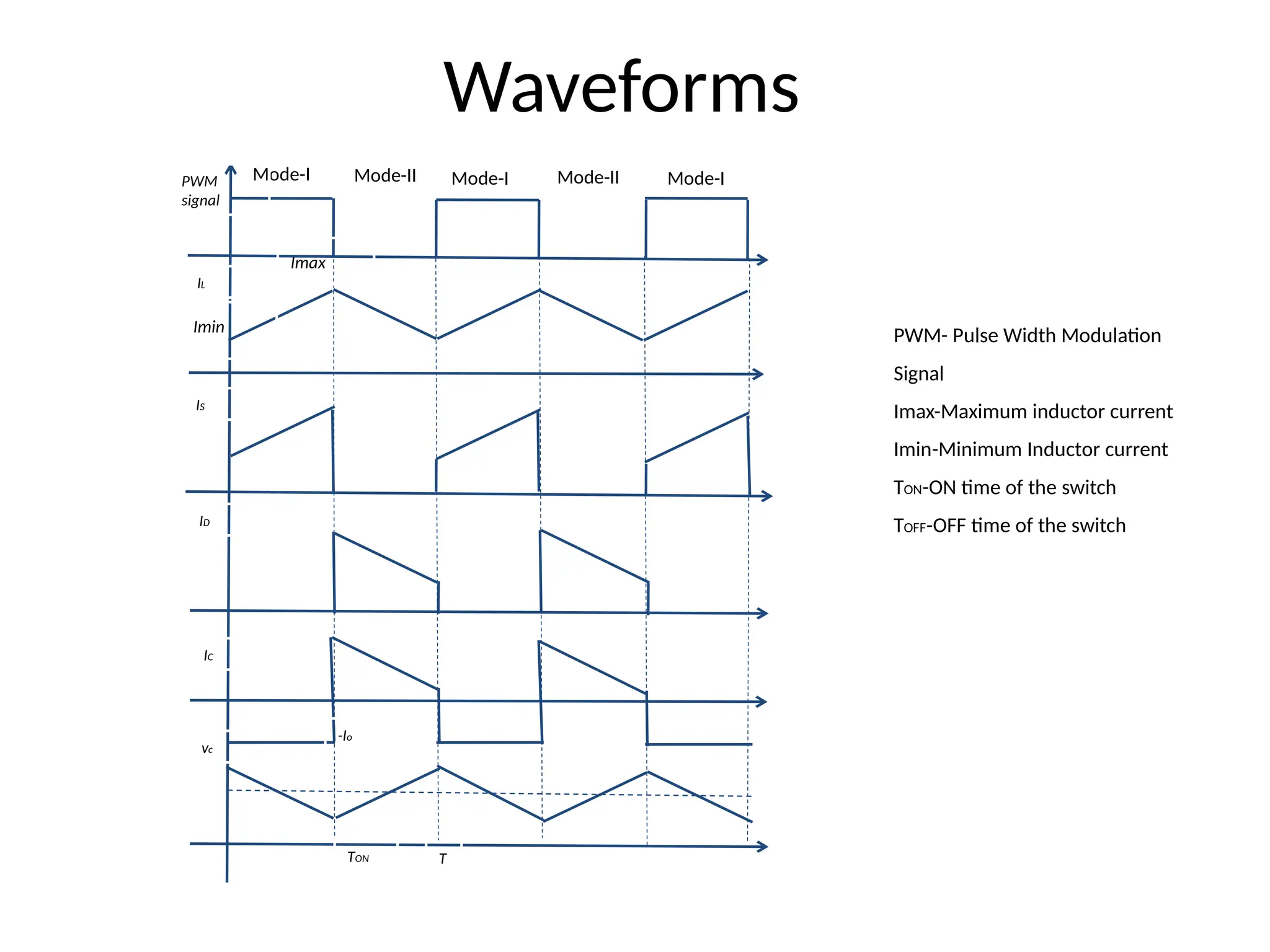
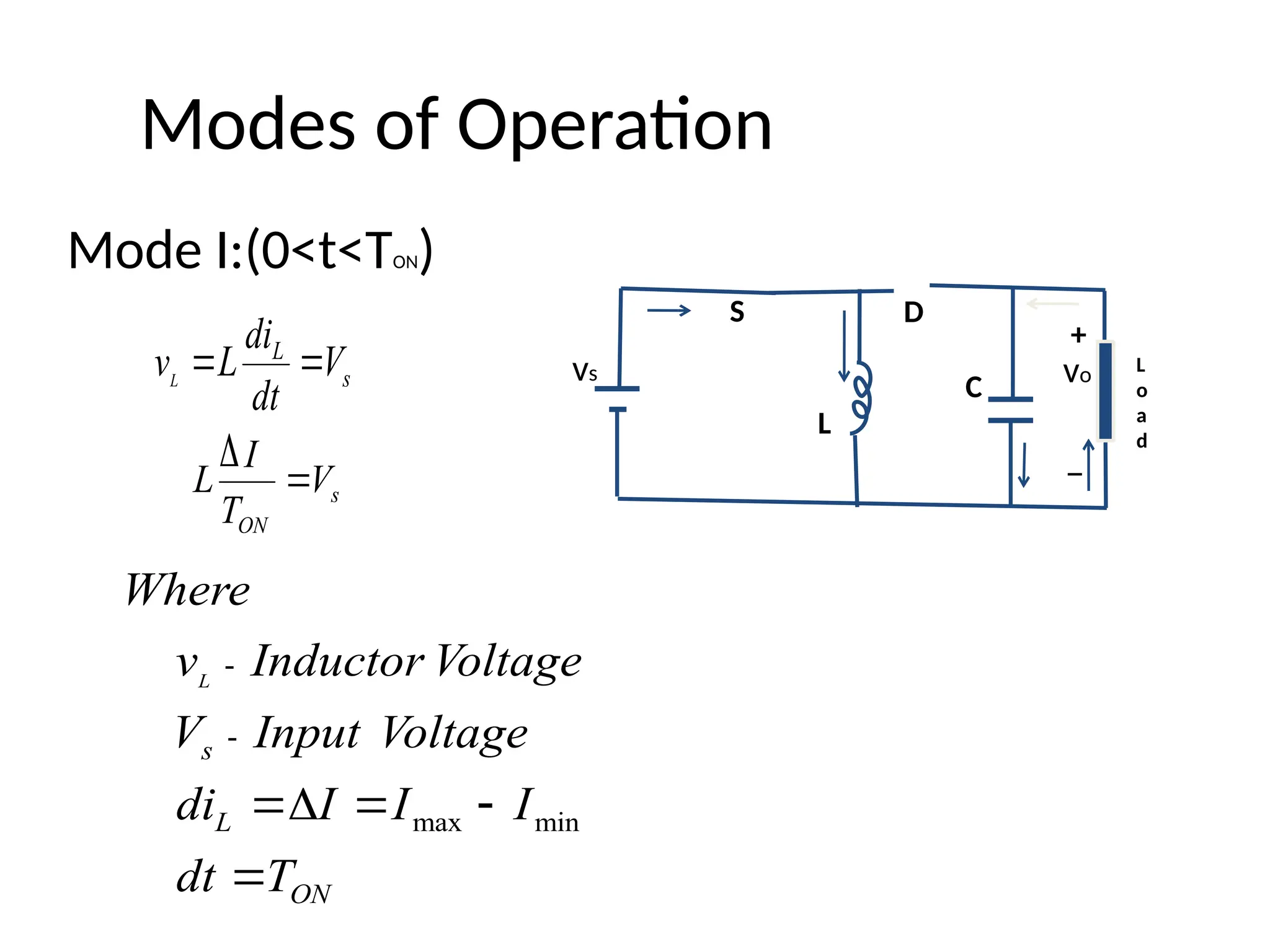
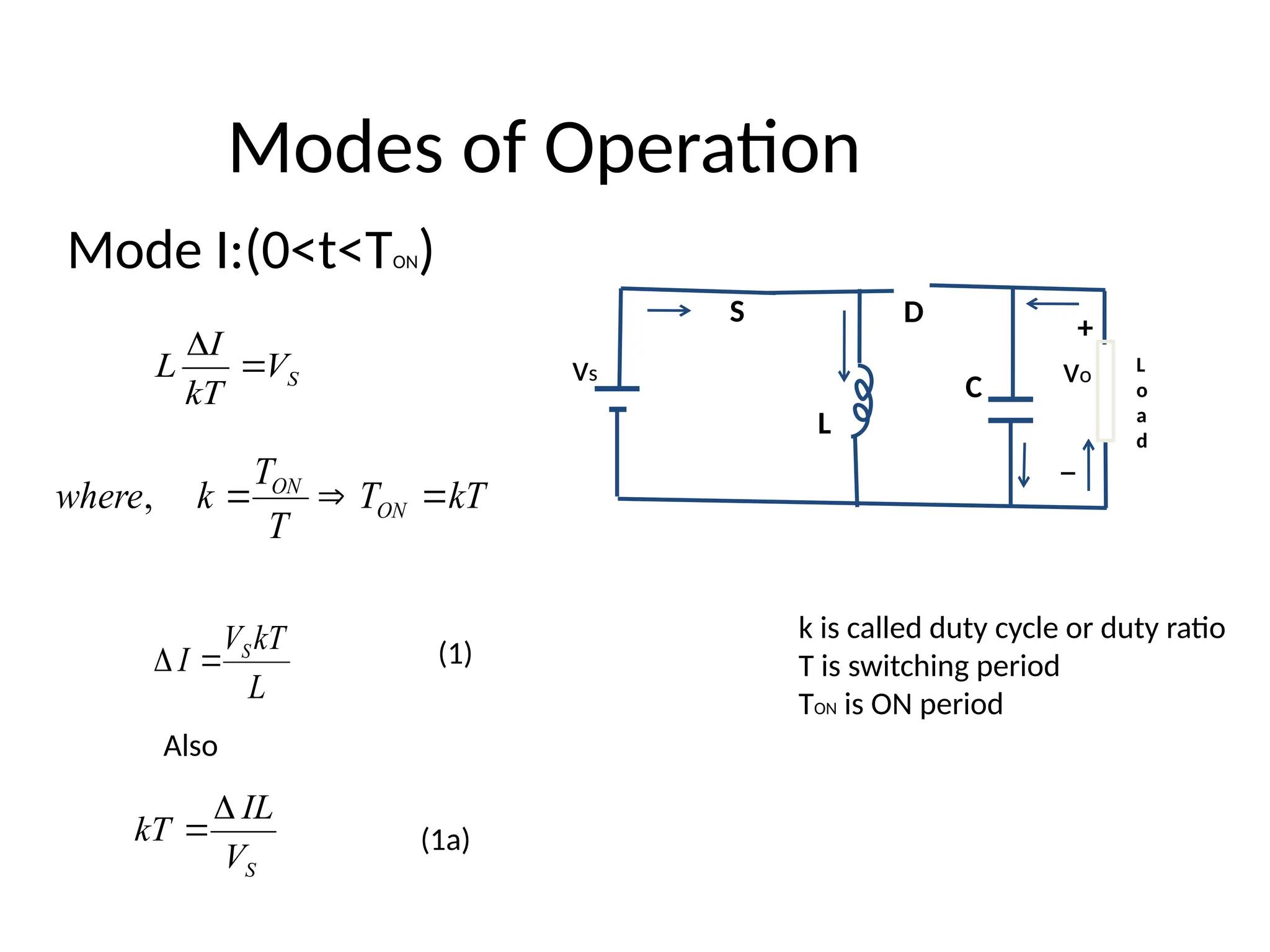
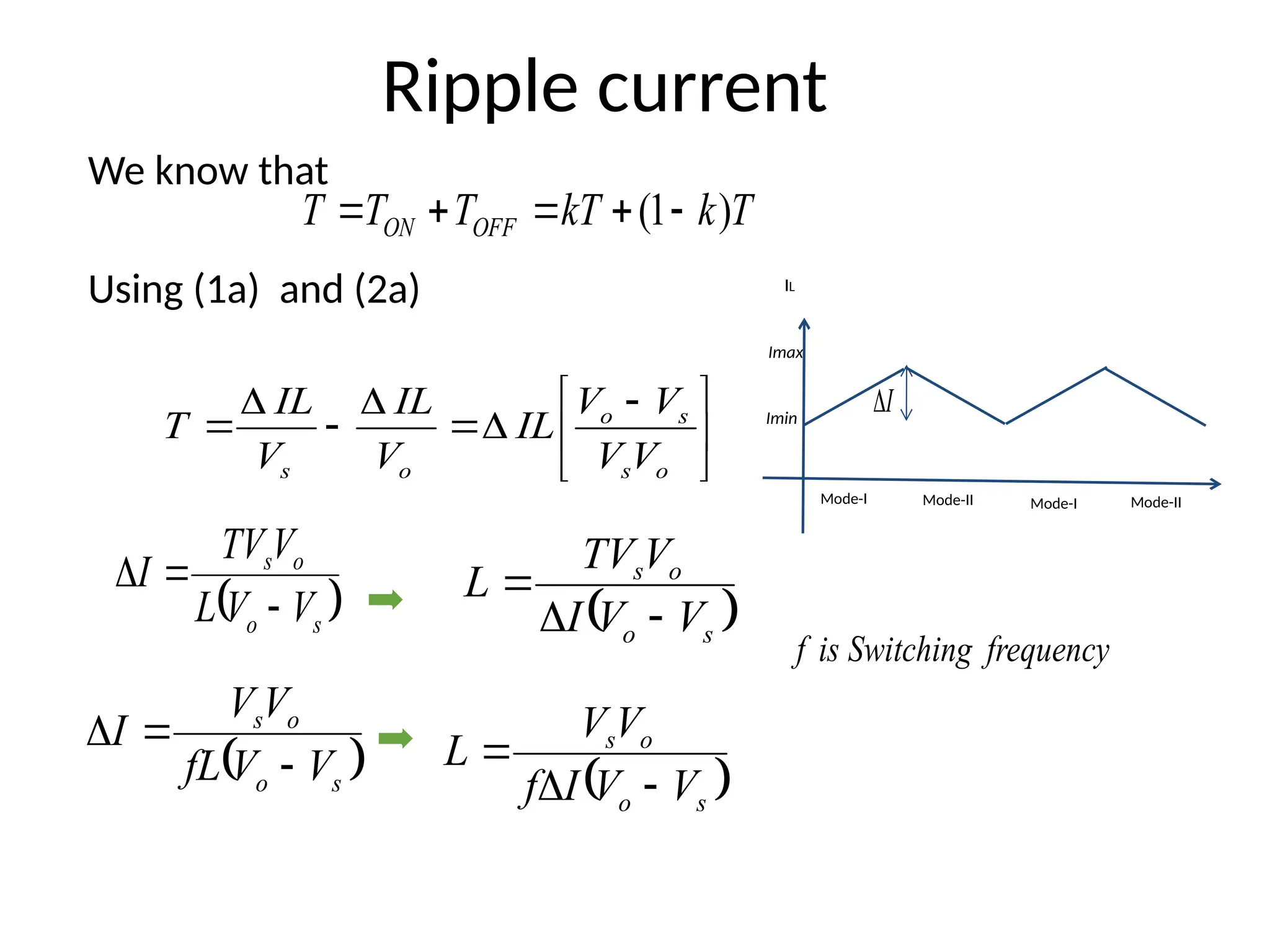
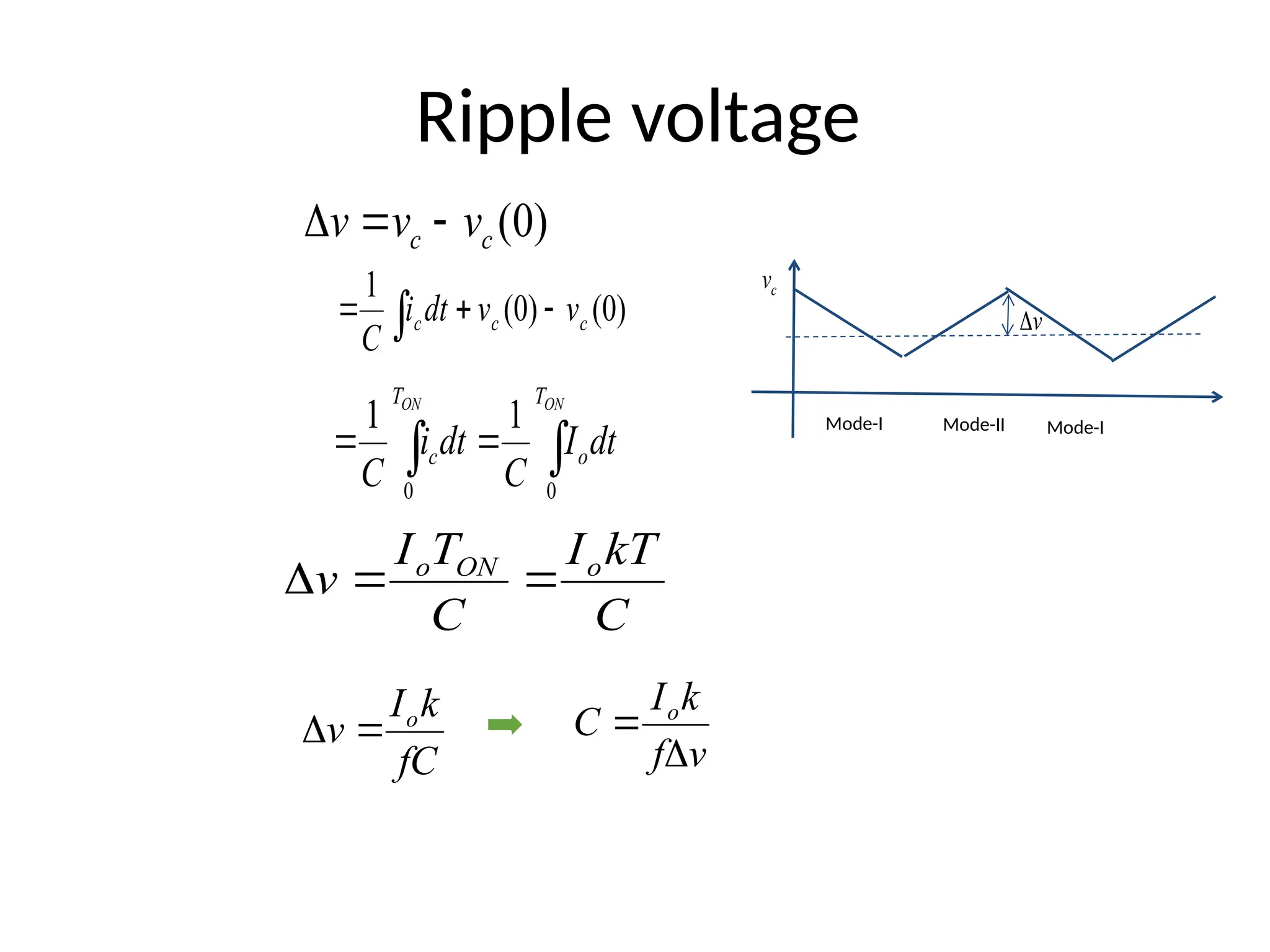
The document provides an introduction to a DC-DC buck-boost converter, explaining its function to step down and step up voltage through two operational modes involving a switch, inductor, capacitor, and diode. It discusses the operation modes, waveforms, voltage output calculations, and establishes conditions for continuous conduction by defining critical values of inductor and capacitor. Applications include self-regulating power supplies and automotive power amplifiers.

1. Introduction to DC-DC Buck-Boost Converter
• Steps down and up the voltage
• Output voltage is lesser or greater
than the input voltage
• There are 2 modes, mode 1(switch
ON) and mode 2(switch OFF)
• It consists of a switch, L, C and a
diode, the switch is operated with a
duty ratio of
• The output voltage is negative,
hence called as Inverting Regulator.
T
T
k ON /

vs vo
+
_
D
S
L
C
L
o
a
d
Vs- Input DC voltage
S- Switch ( MOSFET/IGBT/GTO/BJT)
D-Diode
Vo- Output voltage
L-Inductor
C-Capacitor

2. Applications
Source: prodctodc.com
Source: roboticsandautomationnewscom
Source: prodctodc.com
Self regulating power
supply
Automotive
Power amplifier
Adaptive control
Source: go.gale.com
Battery Power System
Source: bpsbattery.com
DC motor drives
Source: myoutube.com

3. Modes of Operation
Mode I
• During this mode, S
is closed and D is
open
• L stores energy
Mode II
• During this mode, D is
turned ON and S is
turned OFF
• L dissipates its energy
vs vo
+
_
D
S
L
C
L
o
a
d
vs vo
+
_
D
S
L
C
L
o
a
d

4. Waveforms
Mode-I Mode-II Mode-I Mode-I
Mode-II
Imin
Imax
PWM
signal
IL
IS
ID
IC
vc
TON T
-Io
PWM- Pulse Width Modulation
Signal
Imax-Maximum inductor current
Imin-Minimum Inductor current
TON-ON time of the switch
TOFF-OFF time of the switch

5. Modes of Operation
Mode I:(0<t<TON)
s
L
V
dt
di
L
vL


s
ON
V
T
I
L 

ON
L
s
T
dt
I
I
I
di
Voltage
Input
V
Voltage
Inductor
v
Where
L







min
max
vs vo
+
_
D
S
L
C
L
o
a
d

6. Modes of Operation
Mode I:(0<t<TON)
(1)
S
V
kT
I
L 

L
kT
V
I S


kT
T
T
T
k
where ON
ON



,
S
V
IL
kT

 (1a)
Also
k is called duty cycle or duty ratio
T is switching period
TON is ON period
vs vo
+
_
D
S
L
C
L
o
a
d

7. Modes of Operation
Mode II : (TON<t<T)
(2) Also
o
L
V
dt
di
L 
o
OFF
V
T
I
L 
 )
(

o
V
T
k
I
L 



)
1
(
L
T
k
V
I o )
1
( 



T
k
T
T
T
T
where OFF
ON
OFF )
1
(
, 




o
V
IL
T
k



 )
1
( (2a)
vs vo
+
_
D
S
L
C
L
o
a
d

8. Output voltage
Equating volt time equivalents, (1) and (2)
L
T
k
V
L
kT
V o
S )
1
( 


k
k
V
V S
o



1
T
k
V
kT
V o
S )
1
( 


T
k
V
kT
V o
s )
1
( 


T
k
V
kT
V o
s )
1
( 



9. Ripple current
We know that
Using (1a) and (2a)
T
k
kT
T
T
T OFF
ON )
1
( 









 






o
s
s
o
o
s V
V
V
V
IL
V
IL
V
IL
T
 
s
o
o
s
V
V
L
V
TV
I



Imin
Imax
Mode-I Mode-II Mode-I Mode-II
IL
I

frequency
Switching
is
f
 
s
o
o
s
V
V
I
V
TV
L



 
s
o
o
s
V
V
fL
V
V
I



 
s
o
o
s
V
V
I
f
V
V
L




10. Ripple voltage
)
0
(
c
c v
v
v 


)
0
(
)
0
(
1
c
c
c v
v
dt
i
C


 
C
kT
I
C
T
I
v o
ON
o



fC
k
I
v o



 

ON
ON T
o
T
c dt
I
C
dt
i
C 0
0
1
1
v

c
v
Mode-I Mode-II Mode-I
v
f
k
I
C o



11. Condition for continuous conduction
• In order to obtain the continuous inductor
current, the inductor and capacitor values
should be more than a particular value
known as critical values (Lcr and Ccr)
• These values are obtained by equating the
ripple current to 2 times the load current and
the ripple voltage to 2 times the load voltage.

12. Derivation of Lcr and Ccr
o
o
V
fC
k
I
v 2



Rf
k
C
C cr
2


R is load resistance
o
o
V
RfC
k
V
2

  o
s
o
o
s
I
V
V
fL
V
V
I 2




  R
V
V
V
fL
V
V o
s
o
o
s
2


 
s
o
s
cr
V
V
f
R
V
L
L



2

13. Thank you