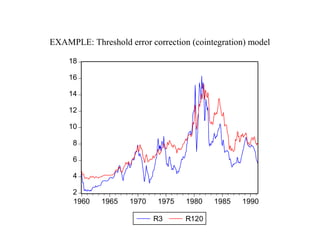
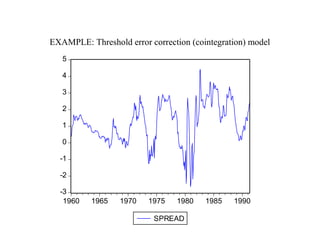
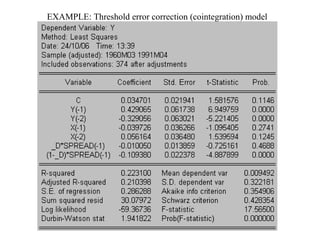
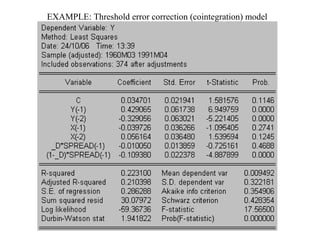
Threshold Autoregressive (TAR) models allow for movements between regimes that are governed by an observed variable. A TAR model contains different parameters depending on whether the state-determining variable is above or below a certain threshold. A self-exciting TAR (SETAR) model occurs when the state-determining variable is a lag of the dependent variable. There are many possible variations of the basic TAR model, including models with switching in some but not all parameters, models with more than two regimes, and models with different threshold variables or dynamic specifications.

1. Threshold Autoregressive (TAR) Models
• Movements between regimes governed by an observed variable.
• TAR model:
• Where st-k
is the state determining variable.
• The integer k determines with how many lags does the state-
determining variable influences the regime in time t.
• When st-k
= yt-k
we have a self-exciting TAR (SETAR) model:
• There are many possible variations of this simple model.



≥++
<++
=
−−
−−
rsifuy
rsifuy
y
kttt
kttt
t
2122
1111
φµ
φµ



≥++
<++
=
−−
−−
ryifuy
ryifuy
y
kttt
kttt
t
2122
1111
φµ
φµ

2. Threshold Autoregressive (TAR) Models
• Example: when st-k
= yt-k
we have a self-exciting TAR (SETAR) model:
• Consider k = 1. Parameters to be estimated:
µ1, µ2,σ1,σ2,
– r
• Estimation method: least squares with r estimated by a grid search.
• There are many possible variations of this simple model:
• Switching in only some of the parameters
• More than 2 regimes
• Different threshold variables
• Alternative dynamic specifications
Can use AIC or other information criteria to select models



≥++
<++
=
−−
−−
ryifuy
ryifuy
y
kttt
kttt
t
2122
1111
φµ
φµ

3. EXAMPLE: Threshold error correction (cointegration) model
2
4
6
8
10
12
14
16
18
1960 1965 1970 1975 1980 1985 1990
R3 R120

4. EXAMPLE: Threshold error correction (cointegration) model
-3
-2
-1
0
1
2
3
4
5
1960 1965 1970 1975 1980 1985 1990
SPREAD

5. EXAMPLE: Threshold error correction (cointegration) model
EVIEWS program:
series y = d(r120)
series x = d(r3)
series spread = r120 - r3
scalar th = 3.22
series _d = ( spread(-1) < th )
equation tar.ls y c y(-1) y(-2) x(-1) x(-2) _d*spread(-1) (1-_d)*spread(-1)

6. EXAMPLE: Threshold error correction (cointegration) model

7. EXAMPLE: Threshold error correction (cointegration) model