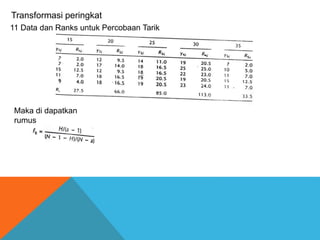
Dokumen ini membahas analisis regresi faktor tunggal untuk menguji pengaruh satu variabel bebas terhadap variabel tergantung. Model regresi linier digunakan untuk memprediksi nilai variabel tergantung berdasarkan nilai variabel bebas. Analisis varians digunakan untuk menguji signifikansi pengaruh variabel bebas tersebut dengan membandingkan jumlah kuadrat antara kelompok dan dalam kelompok.

2. FAKTOR TUNGGAL
Persamaan 1
karena μ muncul dalam semua pengamatan N r muncul hanya ¡n
pengamatan n diambil di bawah perawatan pertama, r2 hanya muncul di
(ne n observasi yang diambil di bawah perawatan kedua
Persamaa2
karena pengamatan dalam pengobatan pertama mengandung r, (ini
memberikan Y. sebagai sisi kanan), p dan r, muncul persis n timcs di y1,
dan semua r lainnya, muncul nol kali, Secara umum, kiri- yang sisi dari
setiap persamaan normal adalah nilai yang diharapkan dari sisi kanan.

3. untuk mencari pengurangan jumlah kuadrat dengan memasang model tertentu
untuk data.
Jumlah derajat kebebasan yang terkait dengan penurunan ¡n jumlah kuadrat,
seperti R (u, r), selalu sama dengan jumlah persamaan yang normal bebas linear.
Sisanya variabilitas belum ditemukan oleh model ditemukan dari
Kuantitas ini digunakan dalam penyebut dari statistik uji untuk H0: r; O.

4. uji signifikansi regresi umum untuk faktor
tunggal
persamaan nomial Kendala O
yang memiliki derajat
kebebasan karena ada
persamaan linear normal

5. analisis faktor tunggal model berbeda
dengan pengobatan = 3
Model regresi setara ¡s
menjadi

6. Analisis varians non parametrik
Uji kruskal walis
Jka n cukup besar, hipotesis nol ditolak

7. Transformasi peringkat
11 Data dan Ranks untuk Percobaan Tarik
Maka di dapatkan
rumus

8. data untuk faktor tunggal diulang Meansure Desain
Menggunakan sampel acak dari beberapa populasi
Pertimbangkan analisis partisi varians dari total jumlah kuadrat
jumlah kuadrat yang dihasilkan dari perbedaan antara subjek dan jabatan kedua
sebagai jumlah kuadrat
SSt=SSbeetween subject + SSwithinsubjects