The document provides an overview of circles in pre-calculus, including definitions, properties, and equations of circles with a focus on their significance in mathematics and real-life applications. It includes group activities aimed at helping students understand the concepts better and highlights the relevance of circles in fields like engineering and astronomy. The standard form for the equation of a circle is also presented, along with several examples.

1. Understanding
Circles
in Pre-Calculus
Marlon L. Dacanay
Mathematics Teacher
Grade 11-STEM

2. "Mathematics is the language in
which God has written the
universe." - Galileo Galilei

3. Color Name!
ACTIVITY 1:
Chord
Diameter
Tangent
Secant
Radius
Center

4. Color Name!
ACTIVITY 1:
Chord
Diameter
Tangent
Secant
Radius
Center

5. Color Name!
ACTIVITY 1:
Chord
Diameter
Tangent
Secant
Radius
Center

6. Color Name!
ACTIVITY 1:
Chord
Diameter
Tangent
Secant
Radius
Center

7. Color Name!
ACTIVITY 1:
Chord
Diameter
Tangent
Secant
Radius
Center

8. Color Name!
ACTIVITY 1:
Chord
Diameter
Tangent
Secant
Radius
Center

9. Color Name!
ACTIVITY 1:
Chord
Diameter
Tangent
Secant
Radius
Center

10. OBJECTIVES:
 Define a circle and write its equation
in standard form.
Derive and manipulate the standard
form of the equation of a circle.
Appreciate the significance of circles
in mathematics and everyday life.

11. Define me!
GROUP
ACTIVITY:

12. Define me!
GROUP
ACTIVITY:
A circle is point set equidistant
of in a plane all points that
center are the given from a
called the.

13. Circle
 A circle is the set of all points
in a plane that are
equidistant from a given
point called the center.

14. Standard Form of the Equation of a Circle
(x - h)² + (y - k)² = r²
where (h, k) is the center and r is the radius
(h, k)
r

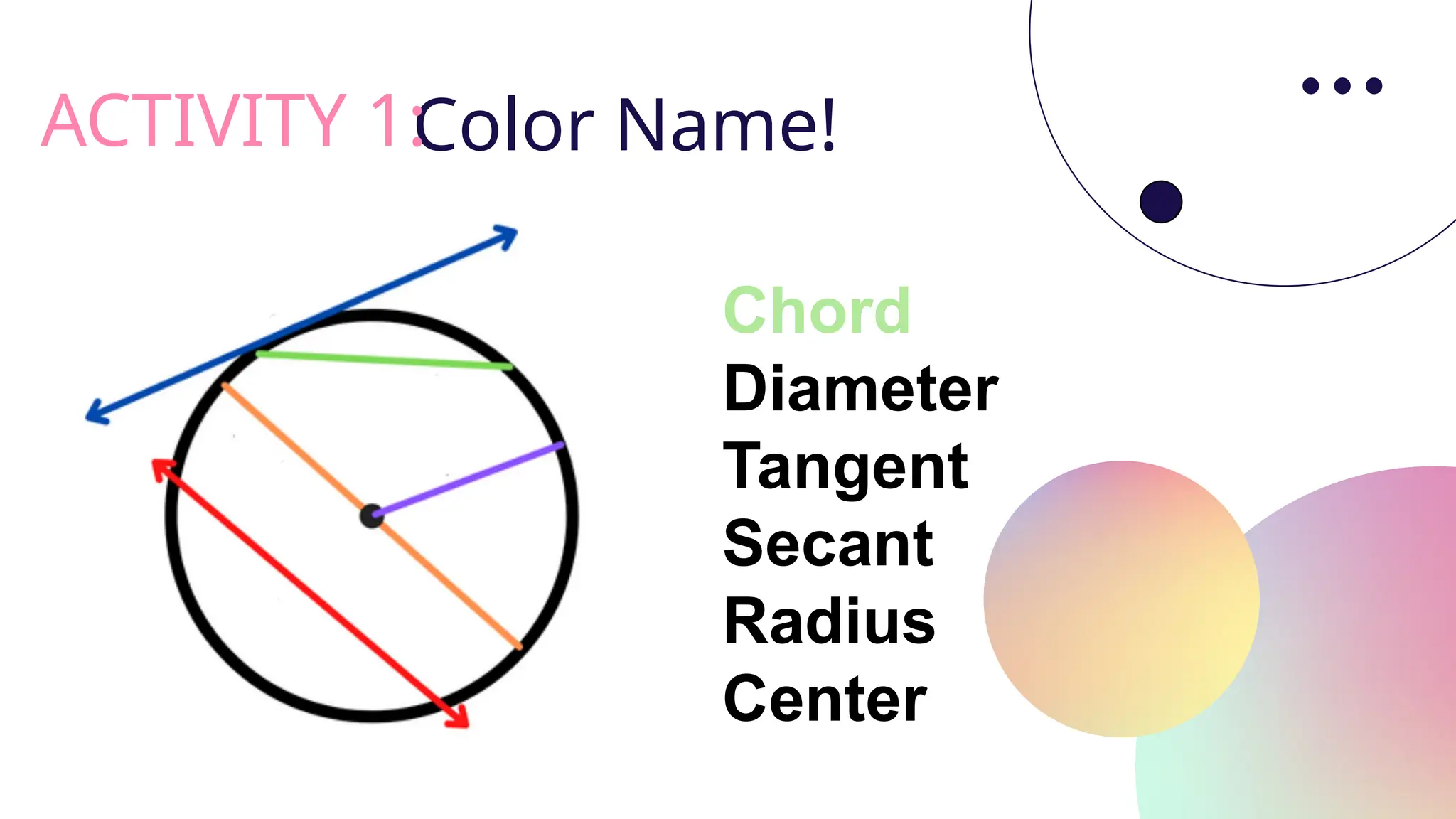
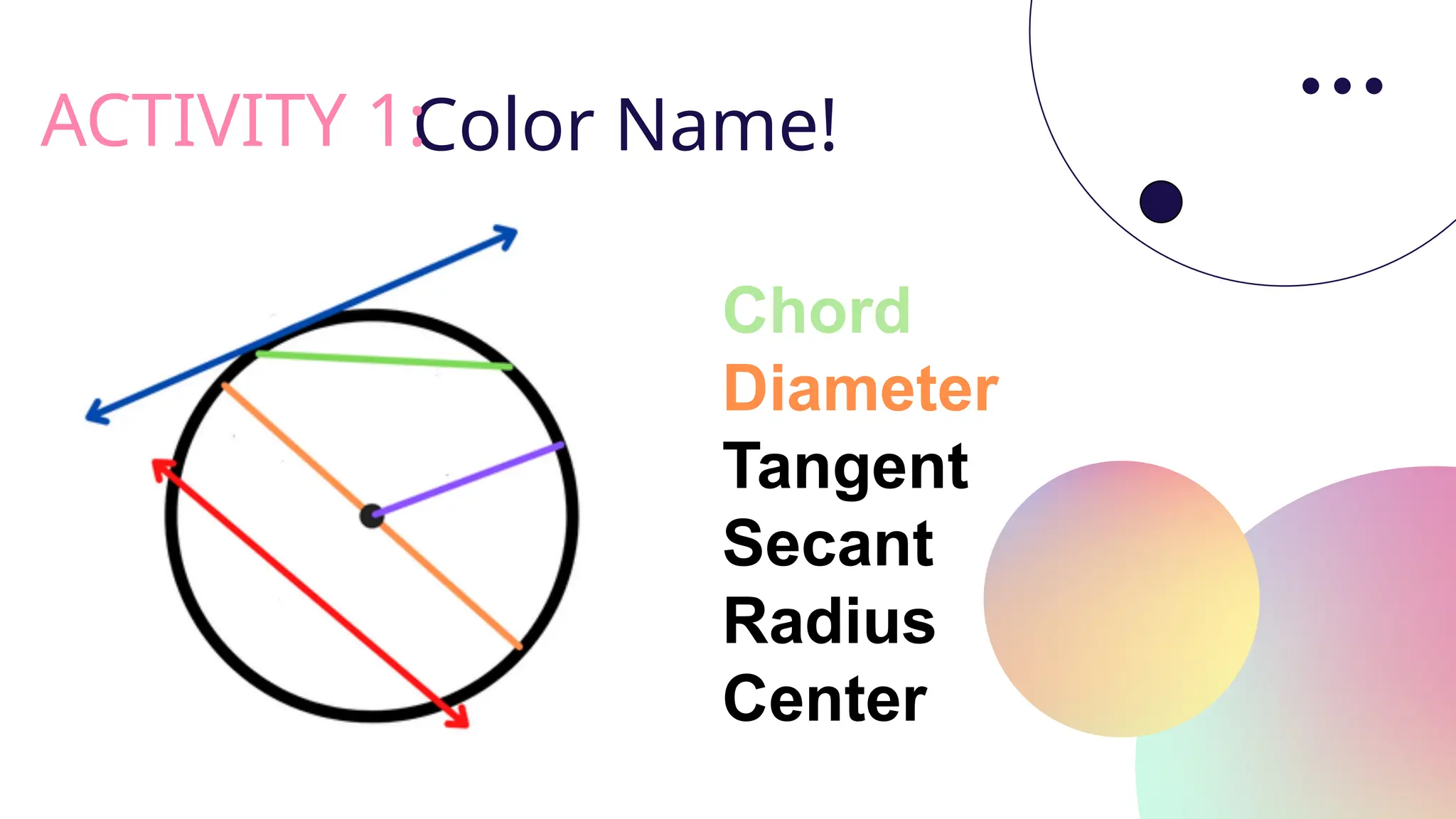
15. Examples:
1: Circle with center at (0, 0)
and radius 5:
(x-0)² + (y-0)² = (5)²
x² + y² = 25
2. Circle with center at (3, -2)
and radius 4:
(x - 3)² + [y -(- 2)]² = (4)²
(x - 3)² + (y + 2)² = 16
(x - h)² + (y - k)² = r²
x² + y² = r²

16. Examples:
3. Center: (0, 0), Radius: 4
(x - h)² + (y - k)² = r²
(x-0²) + (y-0)² = (40) ²
x² + y² = 16
4. Center: (2, -1), Radius: 3
(x - h)² + (y - k)² = r²
(x-2²) + [y-(-1)]² = (3) ²
(x - 2)² + (y + 1)² = 9
(x - h)² + (y - k)² = r²

17. Examples:
5. x² + (y - 3)² = 25
Center: (0, 3), Radius: 5
4. (x + 4)² + y² = 1
Center: (-4, 0), Radius: 1
5. (x - 1)² + (y - 1)² = 4
Center: (1, 1), Radius: 2
(x - h)² + (y - k)² = r²

18. Group Activity: Find My Equation!

19. Group Activity: Find My Equation!
Group 1 Group 2

20. • Understanding the properties
and equations of circles is
fundamental in geometry and
has numerous applications in
various fields.
• Importance: Circles are not just
theoretical concepts but are
widely used in engineering,
astronomy, and everyday
Generalization

21. 1. Astronomy: The orbits of
planets are often
approximated as circles.
2. Engineering: Gears and
pulleys are designed based on
circular motion.
Real-life Relation

22. Relating Across Discipline
Physics: Understanding circular
motion and centripetal force is
crucial in physics, especially in
mechanics. For instance, the
principles of circular motion are
applied when analyzing the
forces acting on a car moving
along a curved path.

23. Isaiah 40:22 (NIV): "He sits enthroned
above the circle of the earth, and its
people are like grasshoppers. He
stretches out the heavens like a canopy,
and spreads them out like a tent to live
in."

24. Any question?