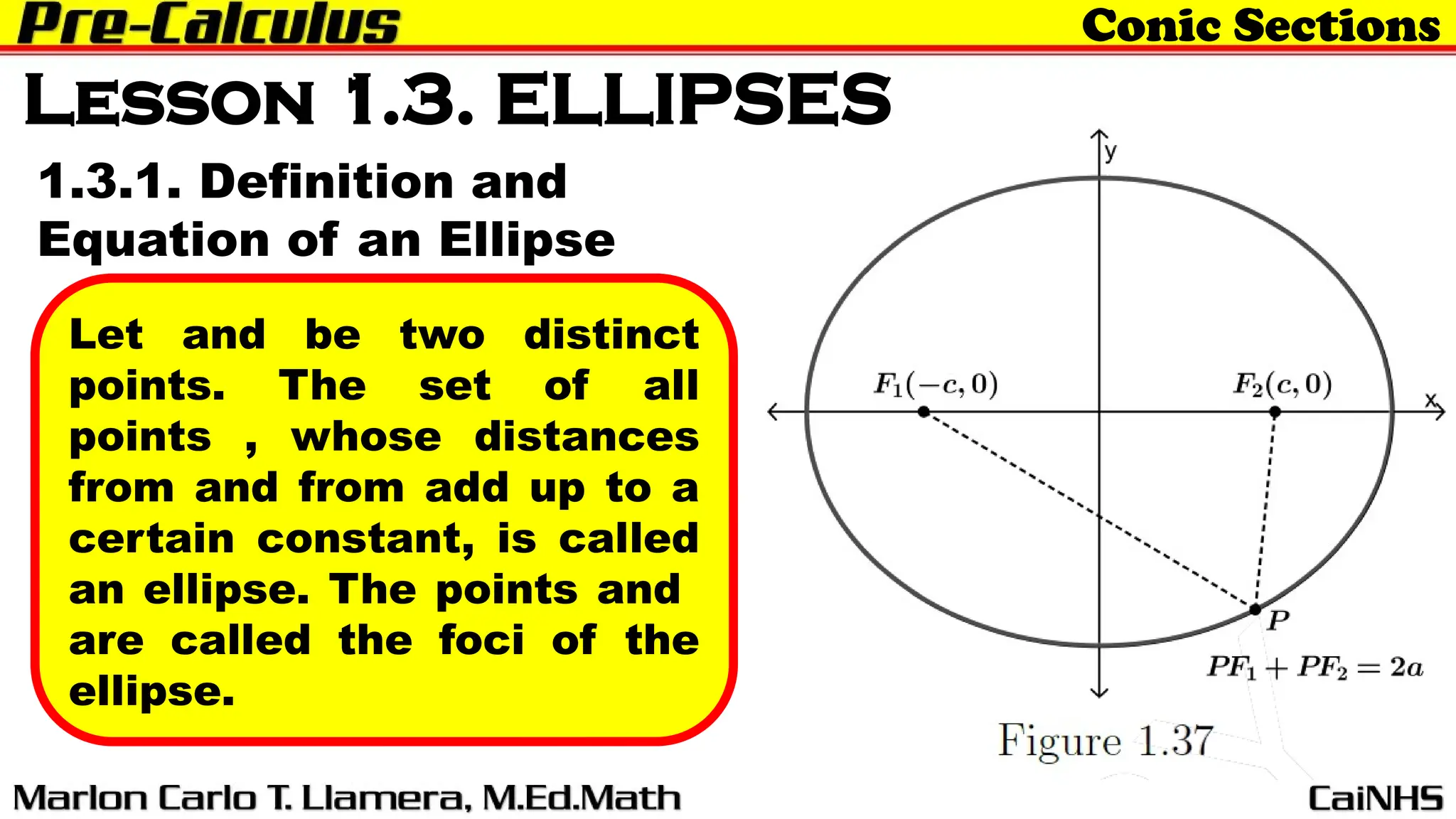
The document outlines a lesson on ellipses as part of conic sections, detailing learning outcomes such as defining an ellipse, determining its standard equation, graphing, and solving problems related to ellipses. It introduces the definition and properties of ellipses, including their geometric characteristics and applications, such as planetary orbits. The lesson aims to provide students with a comprehensive understanding of ellipses in a mathematical context.

1. Conic Sections
Lesson 1.3. ELLIPSES
Learning Outcomes of the Lesson
At the end of the lesson, the student is able to:
1. define an ellipse;
2. determine the standard form of equation of
an ellipse;
3. graph an ellipse in a rectangular coordinate
system; and
4. solve situational problems involving conic
sections (ellipses).

2. Lesson 1.3. ELLIPSES
Lesson Outline
1. Definition of an ellipse
2. Derivation of the standard equation of an
ellipse
3. Graphing ellipses
4. Solving situational problems involving ellipses
Conic Sections

3. Lesson 1.3. ELLIPSES
Introduction
Unlike circle and parabola, an ellipse is one of the
conic sections that most students have not
encountered formally before. Its shape is a bounded
curve which looks like a flattened circle. The orbits of
the planets in our solar system around the sun happen
to be elliptical in shape. Also, just like parabolas,
ellipses have reflective properties that have been
used in the construction of certain structures. These
applications and more will be encountered in this
lesson.
Conic Sections

4. Lesson 1.3. ELLIPSES
1.3.1. Definition and
Equation of an Ellipse
Consider the points and ,
as shown in Figure 1.36.
What is the sum of the
distances of from and
from ? How about the sum
of the distances of (and )
from and from ?
Conic Sections

5. Lesson 1.3. ELLIPSES
1.3.1. Definition and
Equation of an Ellipse
There are other points
such that . The collection
of all such points forms a
shape called an ellipse.
Conic Sections

6. Lesson 1.3. ELLIPSES
1.3.1. Definition and
Equation of an Ellipse
Conic Sections
Let and be two distinct
points. The set of all
points , whose distances
from and from add up to a
certain constant, is called
an ellipse. The points and
are called the foci of the
ellipse.

7. Lesson 1.3. ELLIPSES
Conic Sections