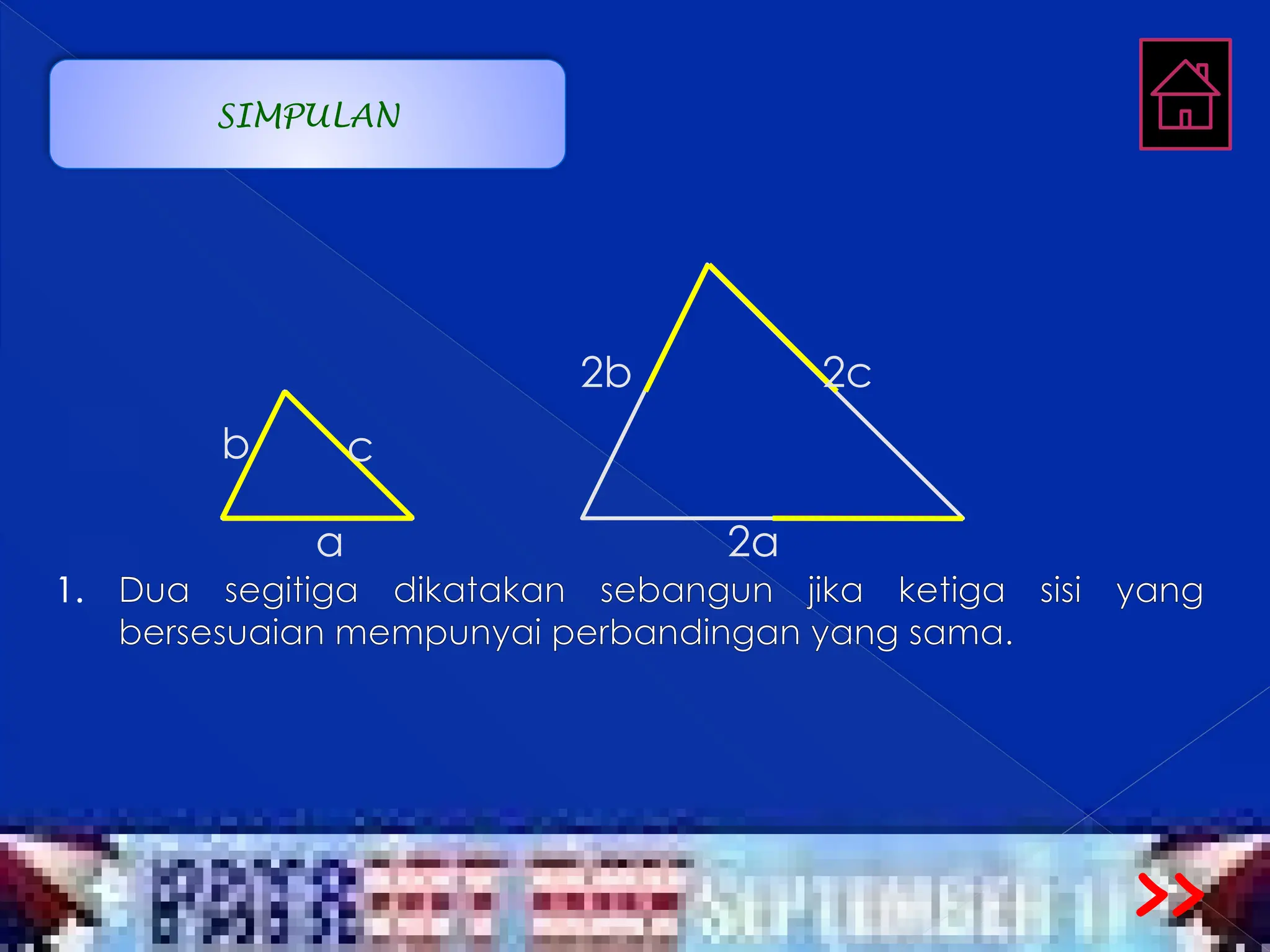
Dokumen ini membahas tentang kesebangunan segitiga pada materi matematika untuk tingkat SMP dan MTs. Penjelasan mencakup pengertian dan sifat-sifat segitiga yang sebangun, serta memberikan contoh dan latihan soal untuk pemahaman. Kesimpulannya, segitiga dikatakan sebangun jika memiliki perbandingan sisi yang sama dan dua pasang sudut bersesuaian yang sama besar.