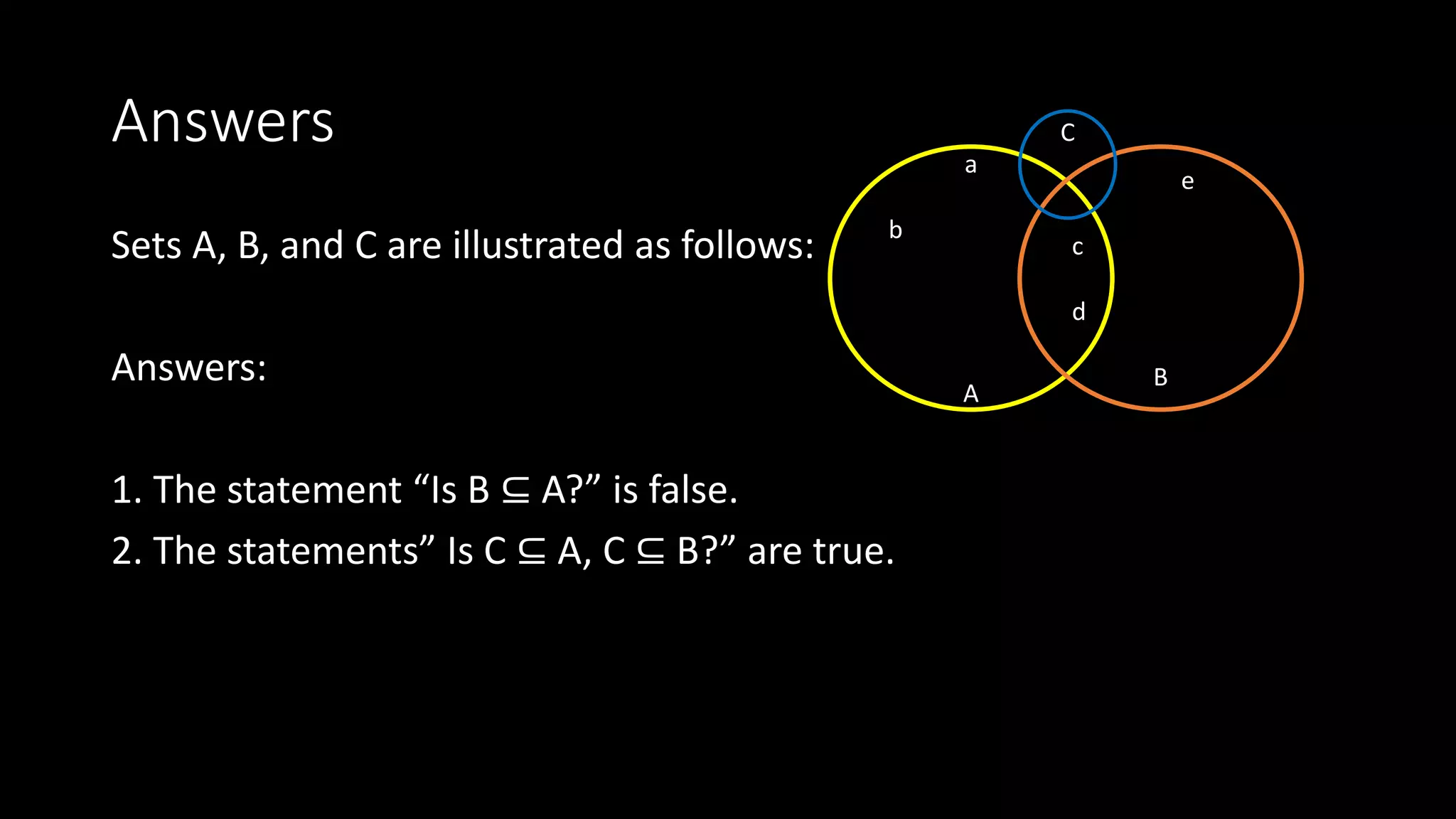
1. A subset is a set where all elements are contained within a larger set, called the superset. A proper subset is where the subset is not equal to the superset. 2. Set union combines all elements contained in both sets. 3. Set intersection filters elements to only those contained in both sets.

1. Set binary operations
Jay Vaughn G. Pelonio, M.A.
Teacher 1

2. Subset and Proper Subset
Let: A={1,2,3,4} ; B={1,2}
Elements {1,2} of set B can be found in set A.
Therefore, Set B is a subset of Set A. B ⊆ A
Subset - a set of which all the elements are contained in another set.

3. Subset and Proper Subset (cont.)
A
3
4
1 2
B
The previous example is illustrated in this figure:
A={1,2,3,4} ; B={1,2}
Since all the elements of set B are in set A, B ⊆ A.
Conversely, Set A is said to be the “superset” set B.
Moreover, All the elements in set B are also in set B.
Therefore, B ⊆ B since B = B.

4. Subset and Proper Subset (cont.)
Proper subset
In the diagram, the following
relationships between sets A and B can
be deduced:
1. B ⊆ A
2. B ≠ A
∴ Set B is proper subset of set A
B ⊂ A.
A
3
4
1,2
B

5. Exercises – Sets and Subsets
• Let:
A={a,b,c,d}; B={c,d,e}; C={ }
• Is B ⊆ A?
• Is C ⊆ A, C ⊆ B?

6. Answers
Sets A, B, and C are illustrated as follows:
Answers:
1. The statement “Is B ⊆ A?” is false.
2. The statements” Is C ⊆ A, C ⊆ B?” are true.
a
b
A
e
c
d
B
C

7. A
Binary Operations - Union
Let: A={1,2,3,4} ; B={1,2} ; C = {3,4,5,6}
1 2
B
3
4
5
6
C
Set Union is the collection of all the
elements in the sets involved.
i.e.:
B U C – Union of B and C:
B = {1,2} C={3,4,5,6}
B U C = {1,2,3,4,5,6,}

8. Binary Operations - intersection
Using the Previous example: A={1,2,3,4} ; B={1,2} ; C = {3,4,5,6}
A
1 2
B
3
4
5
6
C
The intersection of sets is the
collection of elements that are both
present in the sets involved.
i.e.:
𝐴 ∩ 𝐶 – Intersection of A and C
A = {1,2,3,4} C={3,4,5,6}
𝑨 ∩ 𝑪 = {𝟑, 𝟒}
𝑨 ∩ 𝑪 = {𝟑, 𝟒}

9. Exercises:
1. Let: S= {x|x is used at school}
B= {x|x are in the bookstore}
Answer the following questions:
a. Is B ⊆ S ?
b. Write 𝑆 ∪ 𝐵 in set-builder notation
c. Write 𝑆 ∩ 𝐵 in set builder notation

10. Exercises (cont.)
Answers to number 1:
a. Is B ⊆ S? – depending on your point of view, it may be true or false.
b. 𝑆 ∪ 𝐵 may be illustrated this way:
x elements not in B
S
x elements not used
at school
B
x elements used at
school and found in B
S U B= {x|x is used at school or x is in the bookstore}

11. Exercises (cont.)
c. Using the previous Illustration:
x elements not in B
S
x elements not used
at school
B
x elements used at
school and found in B
𝐴 ∩ 𝐵 = {x|x is used at school, x is found in B}

12. Exercises (cont.):
2. Let: A = {1,2,3}
B = {4,5}
Find: a. 𝐴 ∪ 𝐵
b. 𝐴 ∩ 𝐵

13. Exercises (cont.)
2. Let: A = {1,2,3}; B = {4,5}
a. 𝐴 ∪ 𝐵 = {1,2,3,4,5}
b. 𝐴 ∩ 𝐵 = ∅

14. Summary
1. A subset is a set of which all the elements are contained in
another set. Meanwhile, a proper subset is a set which all
elements are contained in another set and its not equal to that
same set.

15. Summary (cont.)
2. Set union is a binary set operation that combines all the elements
that are contained in the sets involved.
3. Set intersection is an operation that filters only the elements that are
contained on both of the sets involved.

16. Assessment – Online Quiz
Let A = {a,b,c,d}; B = {e,f,g}; C = {a,e,f}
Find:
1. A U (B U C) = ?
2. 𝐵 ∩ 𝐶 =?
3. 𝐴 ∩ 𝐵 ∩ 𝐶 =?
4. | 𝐴 ∩ 𝐵 ∩ 𝐶|=?
5. |𝐵 ∩ 𝐶| =?
*submit your answers to my email