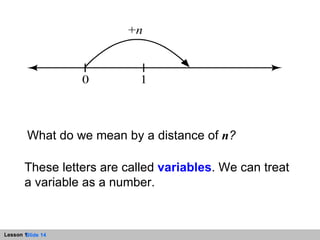
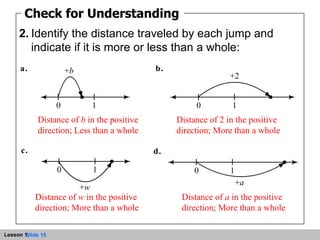
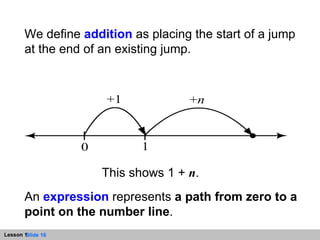
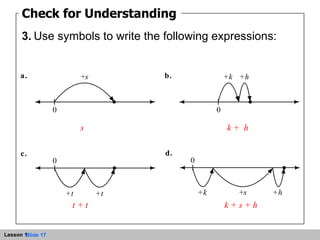
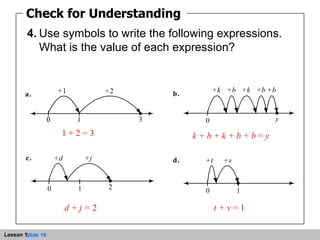
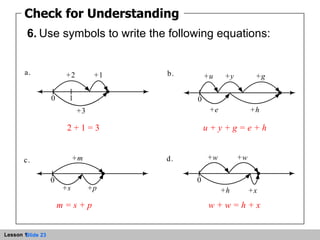
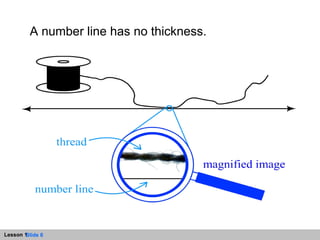
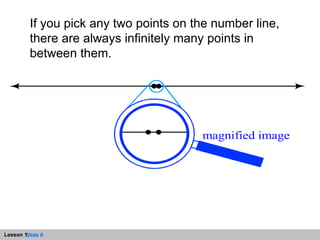
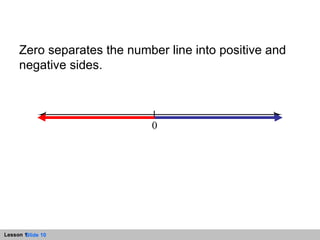
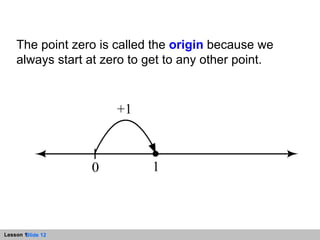
This document introduces key concepts about using the number line to represent expressions and equations: - An expression represents a path from zero to a point on the number line. Variables can be used in expressions to represent unknown numbers. - An equation is a statement that two expressions are equal. Equations can be written symbolically and represented on the number line. - The number line is a straight line that extends infinitely in both directions, with zero as the origin point. Jumps along the number line can represent addition and determine the value of expressions.

1. Chapter 1 Lesson 1 Your First Trip to the Number Line Copyright 2010 MIND Research Institute For use only by licensed users EE.1 Understand that an expression is a path to a point on the number line. EE.2 Understand that an equation is a statement that two expressions are equal. EE.3 Understand that a variable represents an unknown or unspecified number. EE.4 Represent expressions and equations with number line diagrams. Translate number line representations of expressions and equations into symbolic notation.

2. Objectives Use variables in simple expressions and equations. Represent expressions and equations on the number line.

3. Remember from Before How do symbolic notation and the number line fit into our strategy for success this year?

4. Get Your Brain in Gear 1. Count from 0 to 10 as fast as you can. 2. Count by 10’s from 0 to 100 as fast as you can. 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

5. The number line is a perfectly straight line that goes on forever in both directions.

6. A number line has no thickness.

7. The number line is made up of infinitely many points.

8. If you pick any two points on the number line, there are always infinitely many points in between them.

9. There are two important points on the number line that we will use to define where all the other points are located.

10. Zero separates the number line into positive and negative sides.

11. Check for Understanding 1 1. Which of the following points are positive? Which are negative? Explain your reasoning. Check for Understanding The points z and w are negative because they are to the left of 0. The points b , y , and t are positive because they are to the right of 0.

12. The point zero is called the origin because we always start at zero to get to any other point.

13. Jumps can also be shown below the number line. A whole is the distance from 0 to 1 on the number line.

14. What do we mean by a distance of n ? These letters are called variables . We can treat a variable as a number.

15. 2. Identify the distance traveled by each jump and indicate if it is more or less than a whole: Check for Understanding Distance of b in the positive direction; Less than a whole Distance of 2 in the positive direction; More than a whole Distance of w in the positive direction; More than a whole Distance of a in the positive direction; More than a whole

16. We define addition as placing the start of a jump at the end of an existing jump. This shows 1 + n . An expression represents a path from zero to a point on the number line .

17. 3. Use symbols to write the following expressions: Check for Understanding s k + h t + t k + s + h

18. An expression tells us how to get to a point on the number line. That point is called the value of the expression . This expression has a value of 6.

19. 4. Use symbols to write the following expressions. What is the value of each expression? Check for Understanding 1 + 2 = 3 k + b + k + b + b = y d + j = 2 t + v = 1

20. How is this new expression written? How is each expression written using symbols? Consider the following two expressions:

21. Check for Understanding 5 5. Use symbols to write the addition of the following two expressions: Check for Understanding g +f +w

22. By stating that two expressions are equal, we form an equation .

23. 6. Use symbols to write the following equations: Check for Understanding 2 + 1 = 3 u + y + g = e + h m = s + p w + w = h + x

24. Multiple Choice Practice 1. A letter that is used to represent a number is called: the origin a variable a whole an equation

25. Find the Errors 1 Find the Errors No errors. The second jump does not begin at the end of the first jump. Student has +1 less than a whole. The first jump does not start at 0.