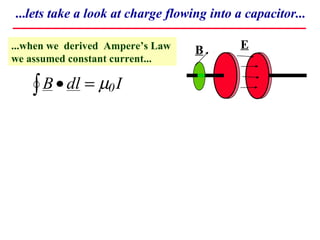
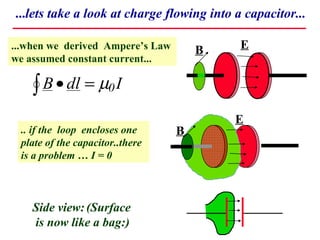
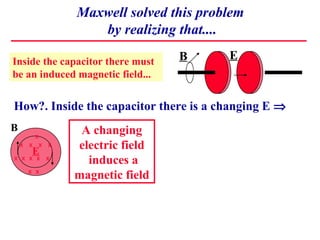
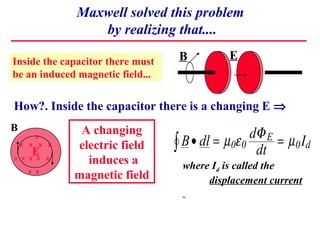
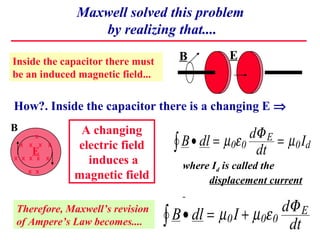
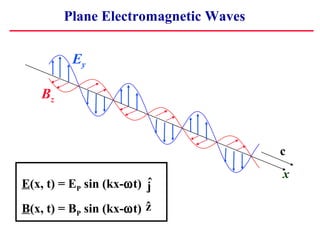
1) Maxwell derived equations showing that changing electric fields induce magnetic fields and vice versa, allowing electromagnetic waves to propagate through space. 2) These electromagnetic waves travel at the speed of light and have oscillating electric and magnetic fields perpendicular to each other and the direction of propagation. 3) Plane electromagnetic waves satisfy the wave equation and can be described by sinusoidal functions with the electric and magnetic fields in phase but oriented at 90 degrees to each other.

1. Chapter 32
The Laws of Electromagnetism
Maxwell’s Equations
Displacement Current
Electromagnetic Radiation

2. The Electromagnetic Spectrum
Radio waves infra ultra
-red -violet γ -rays
µ -wave x-rays

3. The Equations of Electromagnetism
(at this point …)
q
Gauss’ Law for Electrostatics ∫ E • dA = ε0
Gauss’ Law for Magnetism ∫ B • dA = 0
dΦB
Faraday’s Law of Induction ∫ E • dl = − dt
Ampere’s Law ∫ B • dl = µ0 I

4. The Equations of Electromagnetism
Gauss’s Laws ..monopole..
q
1
∫ E • dA = ε0
2
∫ B • dA = 0 ?
...there’s no
magnetic monopole....!!

5. The Equations of Electromagnetism
Faraday’s Law .. if you change a
.. if you change a
dΦ B magnetic field you
magnetic field you
3 ∫ E • dl = − dt induce an electric
induce an electric
field.........
field.........
Ampere’s Law
4 ∫ B • dl = µ0 I .......is the reverse
.......is the reverse
true..?
true..?

6. ...lets take a look at charge flowing into a capacitor...
...when we derived Ampere’s Law B E
we assumed constant current...
∫ B • dl = µ0 I

7. ...lets take a look at charge flowing into a capacitor...
...when we derived Ampere’s Law B E
we assumed constant current...
∫ B • dl = µ0 I
E
.. if the loop encloses one B
plate of the capacitor..there
is a problem … I = 0
Side view: (Surface
is now like a bag:)

8. Maxwell solved this problem
by realizing that....
Inside the capacitor there must B E
be an induced magnetic field...
How?.

9. Maxwell solved this problem
by realizing that....
Inside the capacitor there must B E
be an induced magnetic field...
How?. Inside the capacitor there is a changing E ⇒
B A changing
x
x x x x
E
electric field
x x x x x induces a
x x
magnetic field

10. Maxwell solved this problem
by realizing that....
Inside the capacitor there must B E
be an induced magnetic field...
How?. Inside the capacitor there is a changing E ⇒
B A changing dΦ E
∫ B • dl = µ 0ε 0 dt = µ 0 Id
x
x x x x
E
electric field
x x x x x induces a where Id is called the
x x
magnetic field displacement current

11. Maxwell solved this problem
by realizing that....
Inside the capacitor there must B E
be an induced magnetic field...
How?. Inside the capacitor there is a changing E ⇒
B A changing dΦ E
∫ B • dl = µ 0ε 0 dt = µ 0 Id
x
x x x x
E
electric field
x x x x x induces a where Id is called the
x x
magnetic field displacement current
dΦ E
∫ B • dl = µ 0 I + µ 0ε 0 dt
Therefore, Maxwell’s revision
of Ampere’s Law becomes....

12. Derivation of Displacement Current
dq d( EA )
For a capacitor, q = ε0 EA and I = dt = ε0 dt .
d(Φ E )
Now, the electric flux is given by EA, so: I = ε 0 dt ,
where this current , not being associated with charges, is
called the “Displacement current”, Id.
dΦ E
Hence: I d = µ0 ε0
dt
and: ∫ B • ds = µ0( I + Id )
⇒ ∫ B • ds = µ0 I + µ0ε 0 dΦ E
dt

13. Derivation of Displacement Current
dq d( EA )
For a capacitor, q = ε0 EA and I = dt = ε0 dt .
d(Φ E )
Now, the electric flux is given by EA, so: I = ε 0 dt ,
where this current, not being associated with charges, is
called the “Displacement Current”, Id.
dΦ E
Hence: I d = µ0 ε0
dt
and: ∫ B • dl = µ0( I + Id )
⇒ ∫ B • dl = µ 0 I + µ 0ε 0 dΦ E
dt

14. Maxwell’s Equations of
Electromagnetism
q
Gauss’ Law for Electrostatics
∫ E • dA = ε0
Gauss’ Law for Magnetism
∫ B • dA =0
dΦ B
Faraday’s Law of Induction ∫ E • dl = − dt
dΦ E
Ampere’s Law
∫ B • dl = µ0 I + µ0ε0 dt

15. Maxwell’s Equations of Electromagnetism
in Vacuum (no charges, no masses)
Consider these equations in a vacuum.....
......no mass, no charges. no currents.....
q
∫ E • dA = ε 0 ∫ E • dA = 0
∫ B • dA = 0 ∫ B • dA = 0
dΦB dΦ B
∫ E • dl = − dt ∫ E • dl = − dt
B • dl = µ0 I + µ0ε 0 dΦ E
dΦ E
∫ dt ∫ B • dl = µ0ε 0 dt

16. Maxwell’s Equations of Electromagnetism
in Vacuum (no charges, no masses)
∫ E • dA = 0
∫ B • dA = 0
dΦ B
∫ E • dl = − dt
dΦ E
∫ B • dl = µ0ε 0 dt

17. Electromagnetic Waves
Faraday’s law: dB/dt electric field
Maxwell’s modification of Ampere’s law
dE/dt magnetic field
dΦ E dΦB
∫ B • dl = µ0ε0 dt ∫ E • dl = − dt
These two equations can be solved simultaneously.
ˆ
E(x, t) = EP sin (kx-ωt) j
The result is:
ˆ
B(x, t) = BP sin (kx-ωt) z

18. Electromagnetic Waves
dΦ E dΦ B
∫ B • dl = µ0ε 0 dt ∫ E • dl = − dt
B 
dE E 
dB
dt
dt

19. Electromagnetic Waves
dΦ E dΦ B
∫ B • dl = µ0ε 0 dt ∫ E • dl = − dt
v
B 
dE E 
dB
dt
dt
 
Special case..PLANE WAVES... E = E y ( x ,t ) 
j 
B = Bz ( x ,t )k
∂ 2ψ 1 ∂ 2ψ
satisfy the wave equation = 2 2
∂x 2 ν ∂t
Maxwell’s Solution ψ = A sin( ωt + φ )

20. Plane Electromagnetic Waves
Ey
Bz
c
x
ˆ
E(x, t) = EP sin (kx-ωt) j
ˆ
B(x, t) = BP sin (kx-ωt) z

21. F(x) λ
Static wave
F(x) = FP sin (kx + φ)
k = 2π / λ
k = wavenumber
x λ = wavelength
F(x) λ
Moving wave
F(x, t) = FP sin (kx - ωt )
v
ω = 2π / f
ω = angular frequency
x
f = frequency
v=ω /k

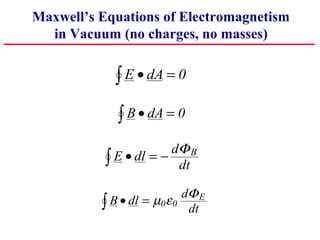
22. F
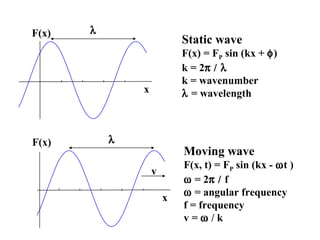
v Moving wave
x F(x, t) = FP sin (kx - ωt )
What happens at x = 0 as a function of time?
F(0, t) = FP sin (-ωt)
For x = 0 and t = 0 ⇒ F(0, 0) = FP sin (0)
For x = 0 and t = t ⇒ F (0, t) = FP sin (0 – ωt) = FP sin (– ωt)
This is equivalent to: kx = - ωt ⇒ x = - (ω/k) t
F(x=0) at time t is the same as F[x=-(ω/k)t] at time 0
The wave moves to the right with speed ω/k

23. Plane Electromagnetic Waves
Ey ˆ
E(x, t) = EP sin (kx-ωt) j
ˆ
B(x, t) = BP sin (kx-ωt) z
Bz
Notes: Waves are in Phase, c
but fields oriented at 900.
k=2π/λ. x
Speed of wave is c=ω/k (= fλ)
c = 1 / ε0µ0 = 3 ×108 m / s
At all times E=cB.