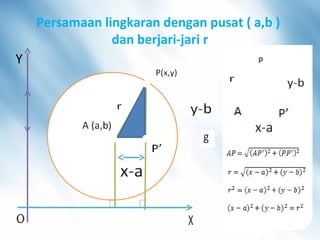
Dokumen ini membahas tentang persamaan lingkaran dengan memberikan contoh rumus lingkaran dengan titik pusat (a,b) dan (0,0) serta soal-soal untuk mengecek pemahaman peserta didik. Peserta didik diajak memahami konsep persamaan lingkaran dan bagaimana rumusnya diperoleh baik untuk lingkaran dengan titik pusat di luar maupun di dalam koordinat.