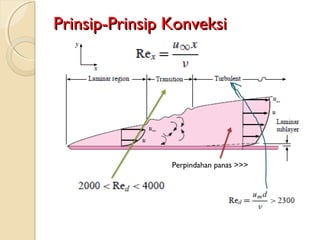
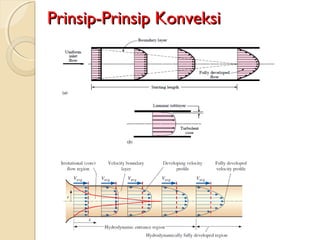
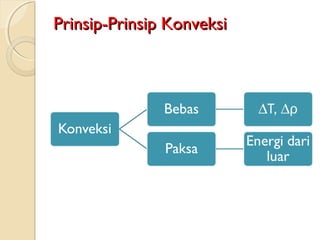
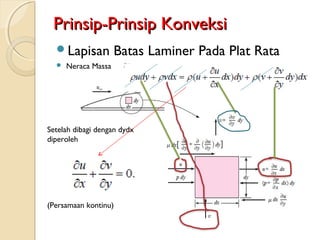
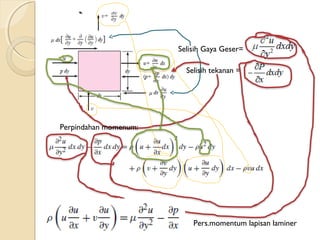
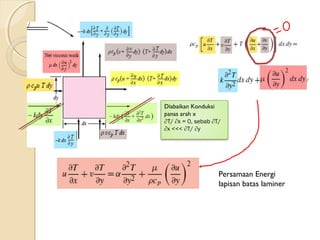
Dokumen ini membahas konsep perambatan panas melalui konveksi, konduksi, dan radiasi, serta pentingnya lapisan batas dalam aliran fluida. Prandtl memperkenalkan konsep lapisan batas pada tahun 1904, yang mempengaruhi analisis gesekan dalam aliran. Penjelasan lanjut termasuk panjang masukan dalam aliran laminar dan turbulen, serta koefisien konveksi dalam keadaan tertentu.

1. PERAMBATANPERAMBATAN / PERPINDAHAN/ PERPINDAHAN
PANASPANAS
((HeatTransferHeatTransfer))
Marfizal, ST, MT
Program Studi Teknik Mesin STITEKNAS Jambi
KONVEKSI
KONDUKSI
RADIASI
KUANTITAS
KALOR
PENGANTAR
PERAMBATAN
KALOR

2. Konsep lapisan batas pertama kali dikemukakan pada tahun 1904 oleh Ludwig Prandtl,
seorang ahli aerodinamika Jerman. Analisa gerak aliran fluida umumnya dapat dibagi
menjadi dua bagian yang pengaruh gesekannya besar yaitu di daerah lapisan batas dan
di luarnya adalah aliran yang tanpa pengaruh gesekan.
Pada aliran fluida bergesekan, pengaruh gesekan akan menimbulkan lapisan batas.
Lapisan Batas adalah daerah yang melingkupi permukaan aliran, dimana tepat di
bawah lapisan batas terdapat hambatan akibat pengaruh gesekan fluida dan tepat di
atas lapisan batas aliran fluida adalah tanpa hambatan, sehingga untuk menganalisa
pengaruh gesekan fluida, penting untuk diketahui konsep tentang lapisan batas
tersebut.
Lapisan BatasLapisan Batas ((Boundary layerBoundary layer))

3. Lapisan batas pada aliran internal akan berkembang terbatas sampai dapat meliputi seluruh
penampang aliran fluida dan hanya terjadi pada daerah di sekitar lubang masuk aliran
sehingga pada umumnya dapat diabaikan dan aliran dianggap seragam. Namun pada aliran
eksternal pertumbuhan lapisan batas tidak terbatas sehingga umumnya pembahasan
perkembangan lapisan batas menjadi sangat penting.
Lapisan batas ini akan berkembang terus sampai suatu panjang tertentu yang disebut
sebagai panjang masukan (entrance length) kemudian lapisan batas tidak dapat
berkembang lagi (Fully developed flow). Untuk aliran internal dan laminar yaitu dengan
Re< 2300 maka panjang masukan, LE adalah fungsi angka Reynold yaitu:
LE/D ≈ 0,06 ρ v D/µ
LE ≈ 0,06 x Re x D ≈138D
Sedangkan untuk aliran internal turbulen, dari hasil percobaan, panjang masukannya
adalah antara 25D atau 40D.
Lapisan Batas (Lapisan Batas (Boundary layer)

4. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Perpindahan panas >>>

5. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi

6. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi

7. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Lapisan Batas Laminer Pada Plat Rata
 Neraca Massa
Setelah dibagi dengan dydx
diperoleh
(Persamaan kontinu)

8.  Selisih Gaya Geser=
Selisih tekanan =
Perpindahan momenum:
Pers.momentum lapisan laminer

9. Diabaikan Konduksi
panas arah x
∂T/ ∂x = 0, sebab ∂T/
∂x <<< ∂T/ ∂y
Persamaan Energi
lapisan batas laminer

10. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Bila pada u∼u∞ dan y∼δ, maka
Sehingga dan
Untuk aliran laminer (u rendah), maka:
Def:
Jadi aliran viskos dan v kecil:
Pengaruh viskos
Pengaruh
konduksi
u∞ =70 m/s T =20 C◦
=293 K p=1 atm, Pada
kondisi cp =1005 J/kg
C and Pr =0◦ .7,
sehingga

11. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
 Batas-batas Termal
Koefisien panas konveksi pada
lapisan batas terma plat rata,
dimana pemanasan dimulai
pada x = xo:
Dimana: v = μ/ρ
Bila xo = 0, pemanasan pada satu titik:
Koefisien konveksi rata pada ruas-ruas plat:
:x/k

12. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Untuk pemansan sepanjang plat :
Bila ∆T dinding dan fluida >>
Tf = suhu lapisan

13. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
 Bula fluks kalor tetap berlaku hubungan:
 Atau dpt dinyatakan fluks kalor dinding dan beda suhu:
 Beda suhu rata-rata sepanjang plat:

14. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Hubungan lain: bila Pr << pada logam
cair, atau Pr>> pada minyak berat
persamaan adalah:

15. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Contoh:Udara pada 27◦C dan 1 atm mengalir
melalui plat dng kec. 2 m/s. Andaikan plat
dipanaskan seluruhnya sampai 60o
C. Hitung : q
pada x= 20 cm dan x= 40 cm. Viscositas
udara pada 27◦C = 1.85×10−5 kg/m· s.
Penyelesaian:
Suhu film:
Sifat fluida (App.3)

16. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Pada x = 20 cm:
Nilai rata-rata koef. h:
Aliran panas adalah:

17. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Andaikan satu satuan kedalam arah z:
Pada x = 40 cm

18. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Contoh:
Hit. ∆T pada sepanjang plat dan tepi belakang
Penyelesaian:
Tf = ?  hitung kondisi aliran bebas
Q = 1 kW
Udara, 27o
C, 1atm, u∞ =
5 m/s
Ukuran plat: 60 x 60 cm

19. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
Pada tepi belakang , gunakan

20. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
 Udara 1 atm dan 300 K mengalir melalui plat bujur sangkar 20 cm
dan kecepatan 20 m/s. Setangah plat terakhir dipanaskan untuk
memerpoleh suhu 350 K. Hitung panas yang hilang pada plat.
 Penyelesaian:
Tentukan suhu T:
Untuk udara diperoleh harga :
Pemanasan dimulai pada posisi x = 0,1 m

21. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
 Lebar plat dipanaskan 0.2 m, sehingga panas yang
ditansfer adalah integrasi sepanjang xo<x<L
 Setelah diintegrasikan diperoleh:
 Nilai rata-rata koefisien perpindahan panas pejang
daerah yang dipanaskan adalah:
 W = lebar plat
 Untuk memeudhkan perhitungan dapat gunakan rumus:
 diperoleh:

22. Prinsip-Prinsip KonveksiPrinsip-Prinsip Konveksi
 Hubungan antara Friksi Fluida dan Perpindahan
Panas
 Def: 