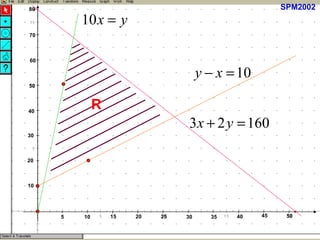
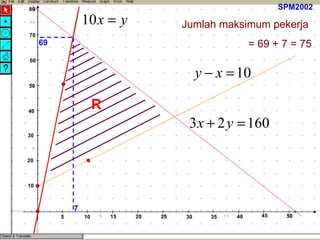
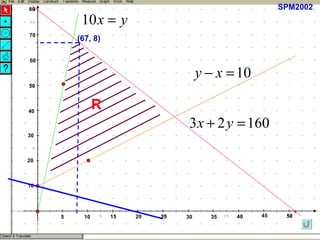
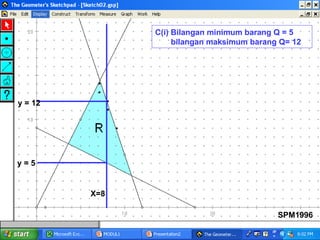
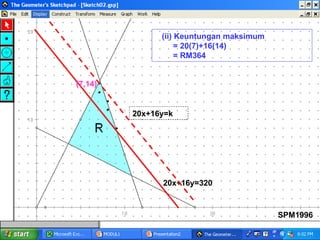
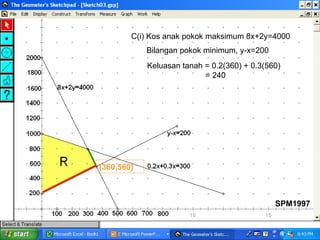
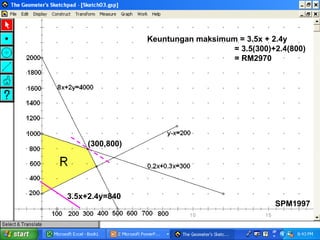
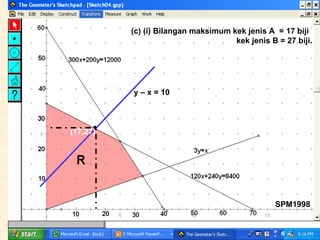
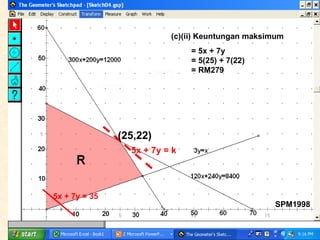
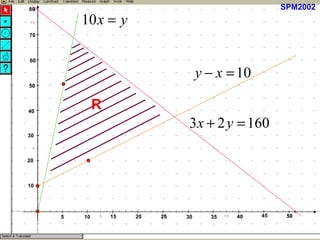
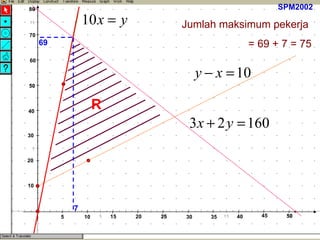
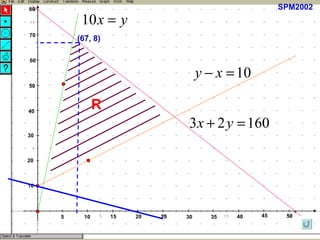
Kilang spm2002 sedang mengambil pekerja baru sebagai penyelia dan operator dengan peruntukan gaji keseluruhan RM32,000. Terdapat syarat bahawa bilangan operator harus melebihi penyelia sebanyak 10 orang dan penyelia mesti sekurang-kurangnya 10% daripada bilangan operator. Berdasarkan ketaksamaan yang ditetapkan, jumlah maksimum pekerja yang dapat diambil ialah 75, dan jumlah maksimum elaun lebih masa yang perlu dibayar adalah RM664.