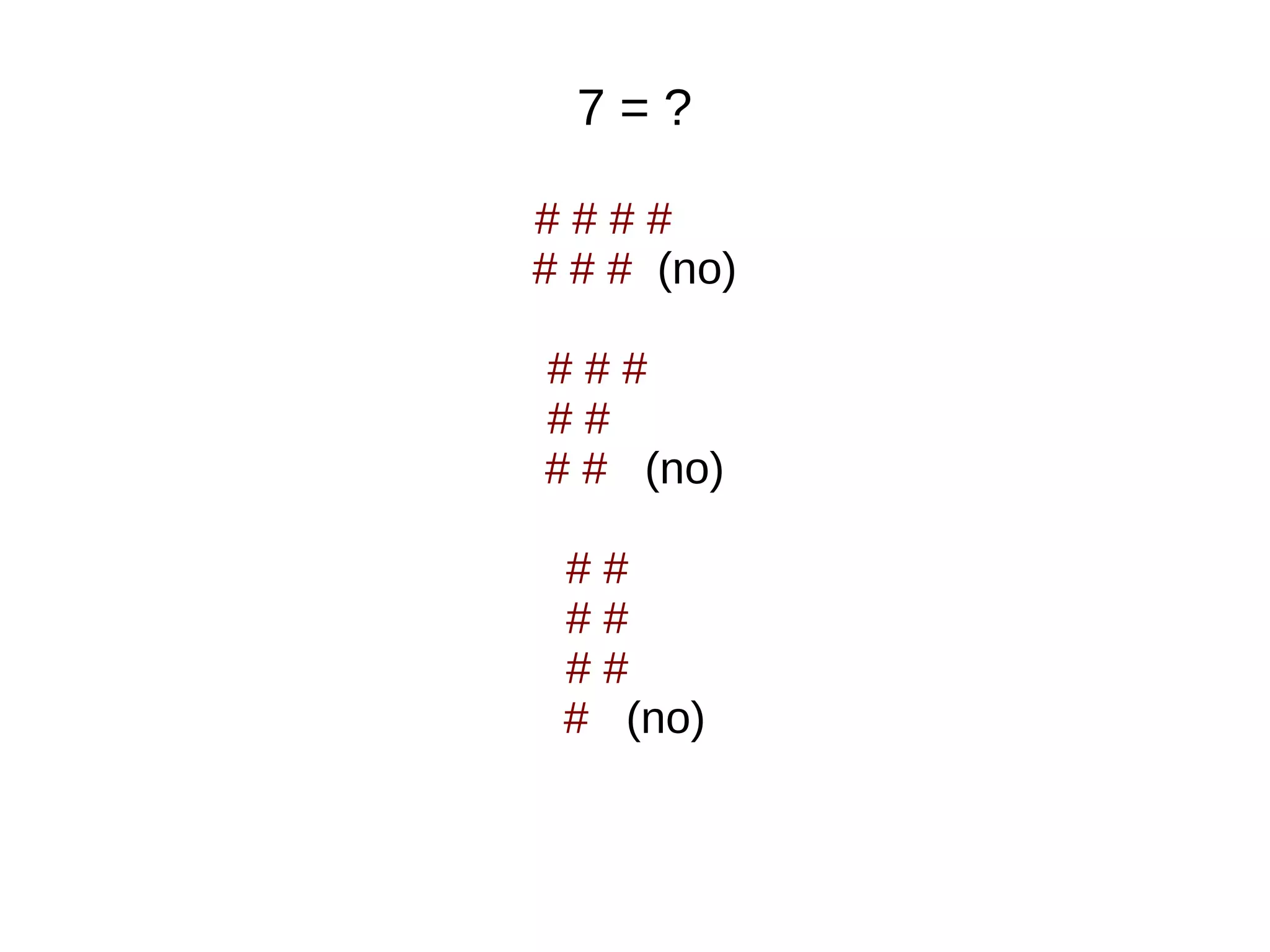
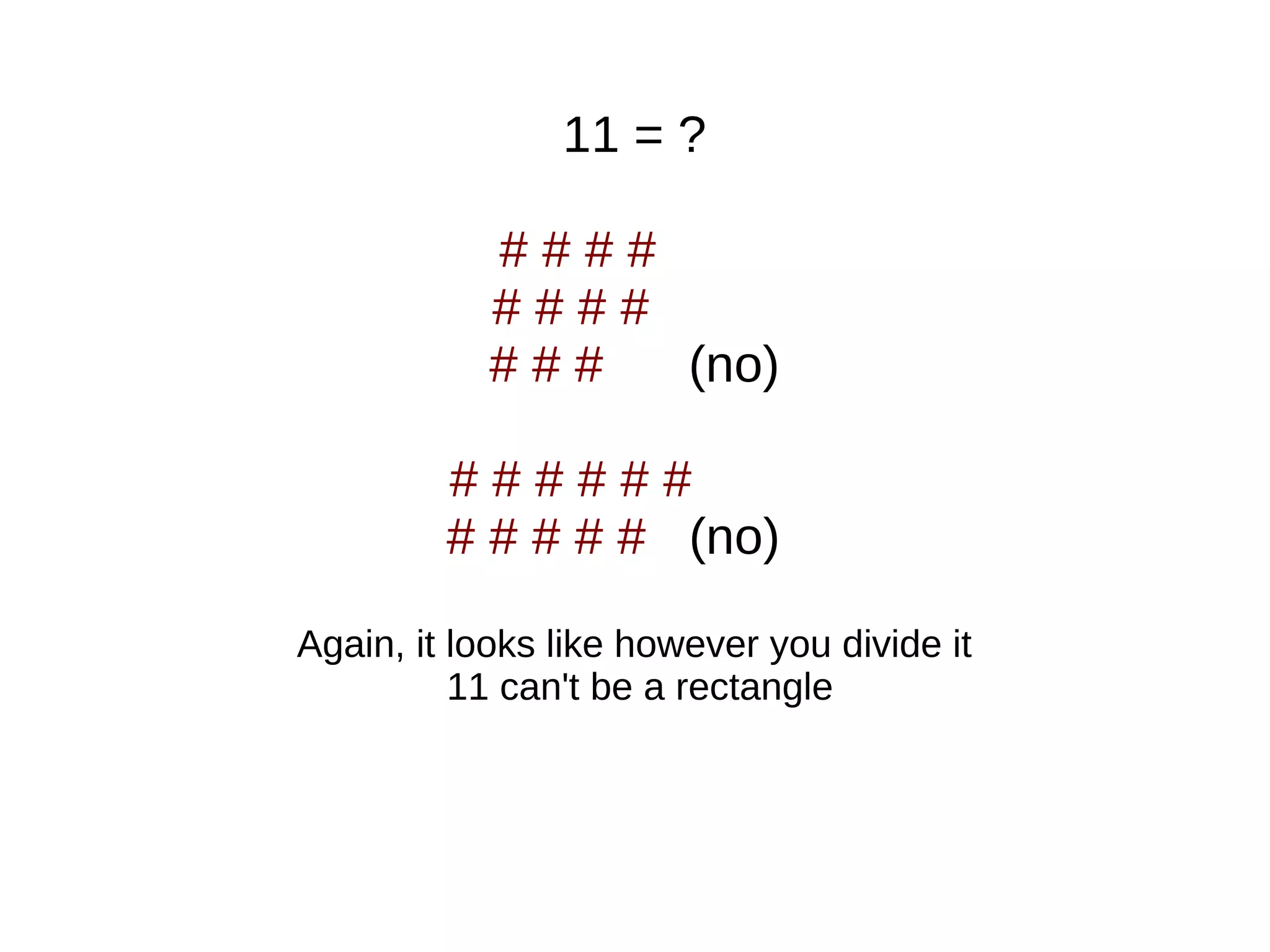
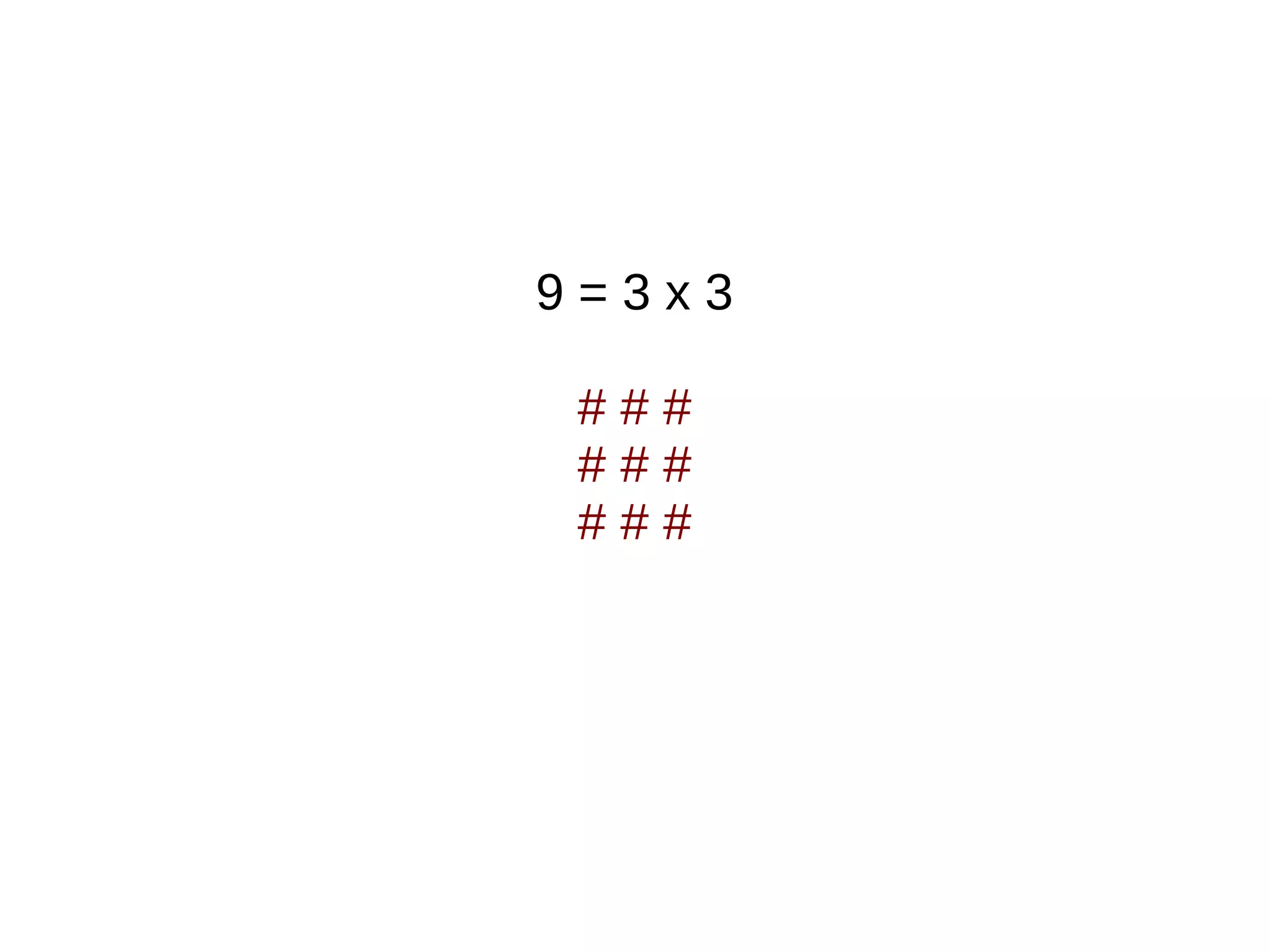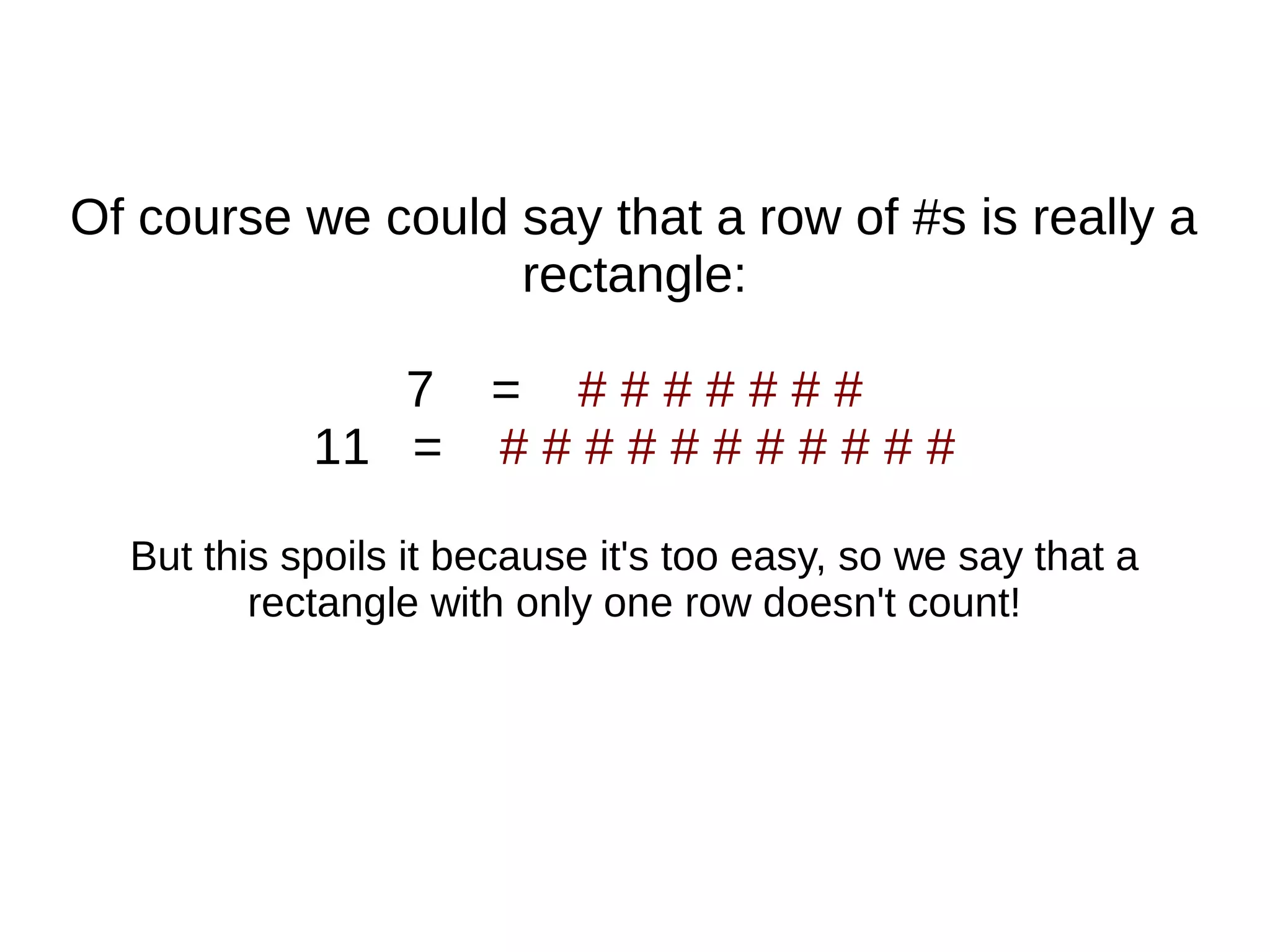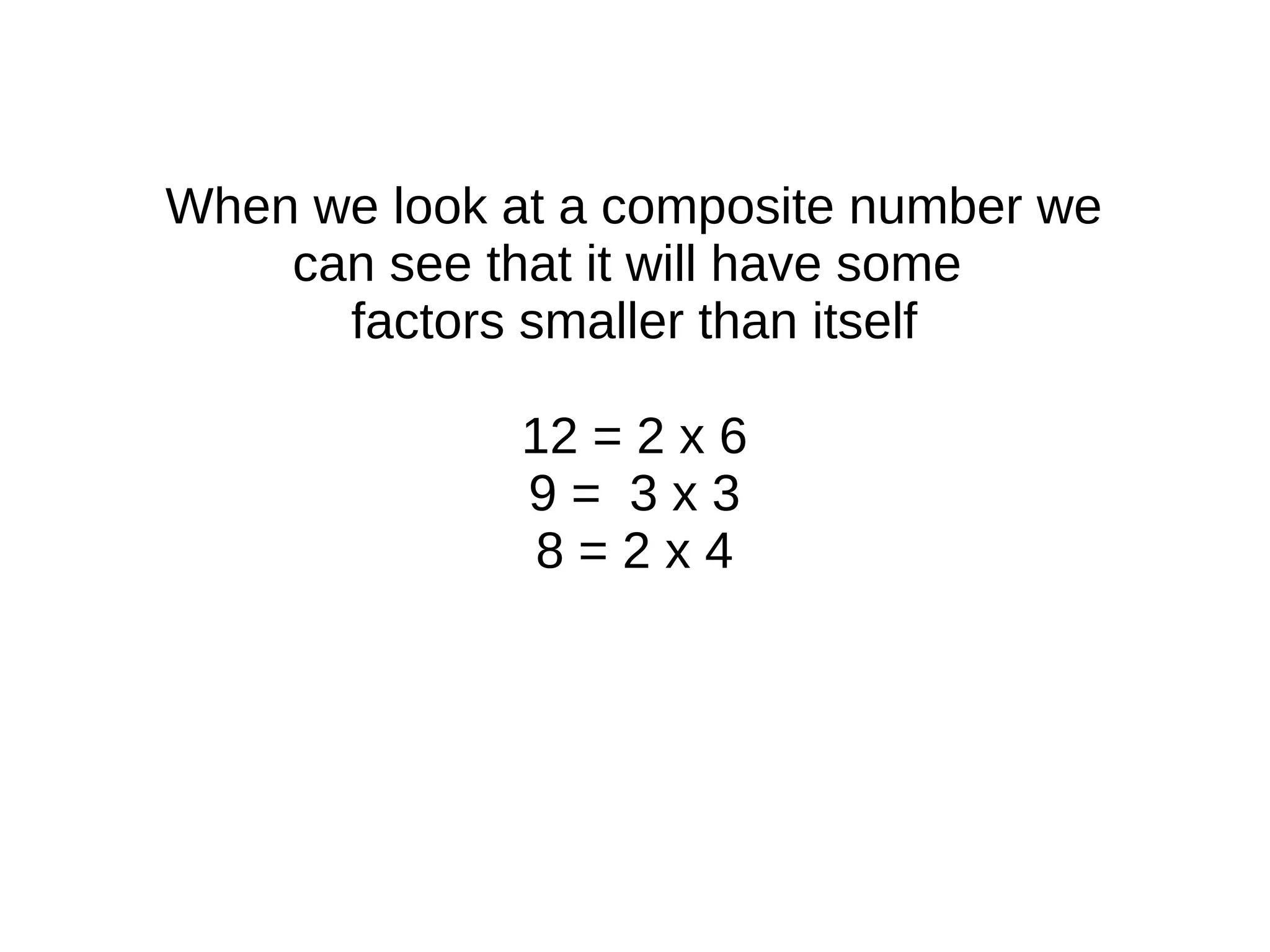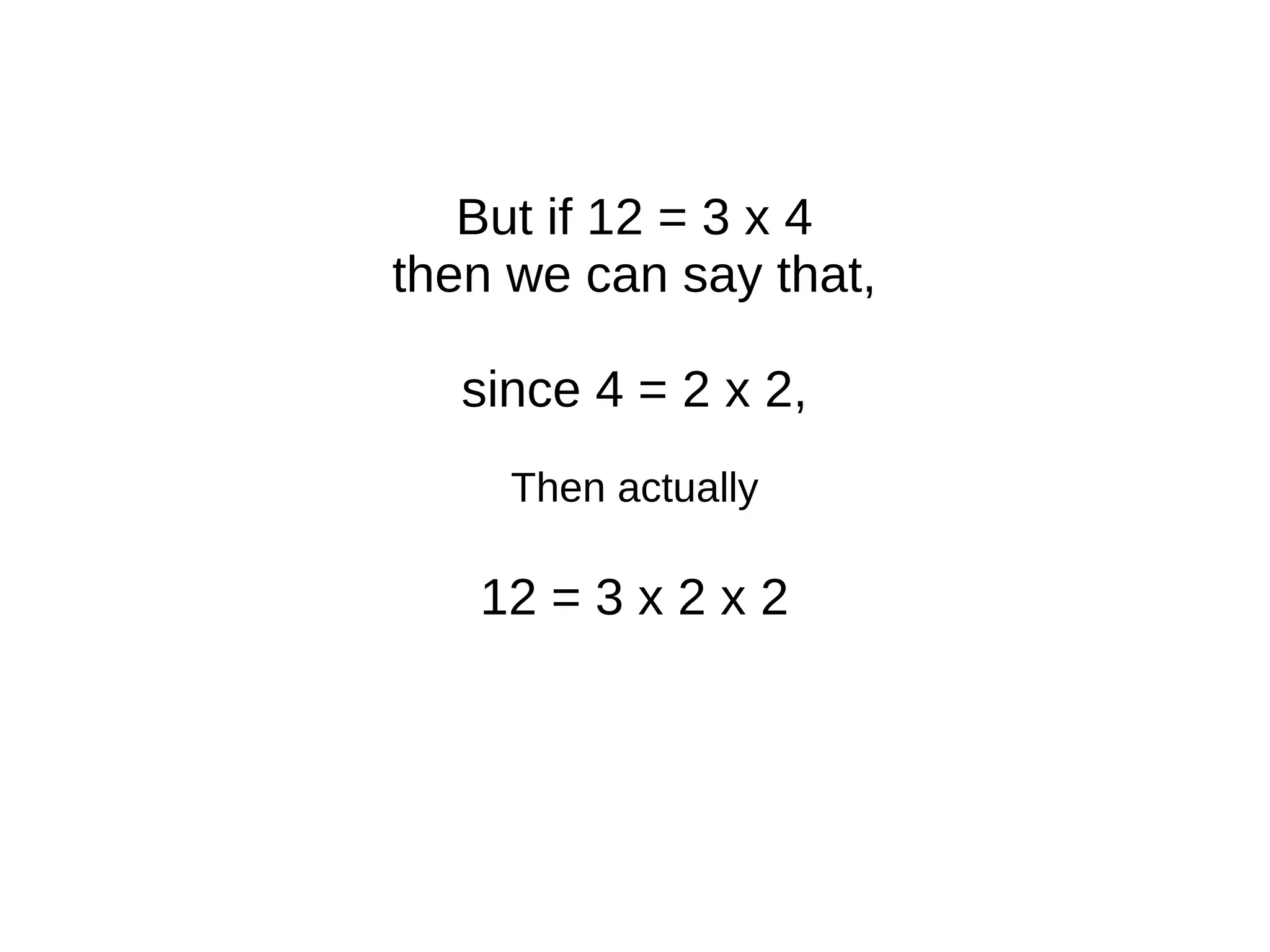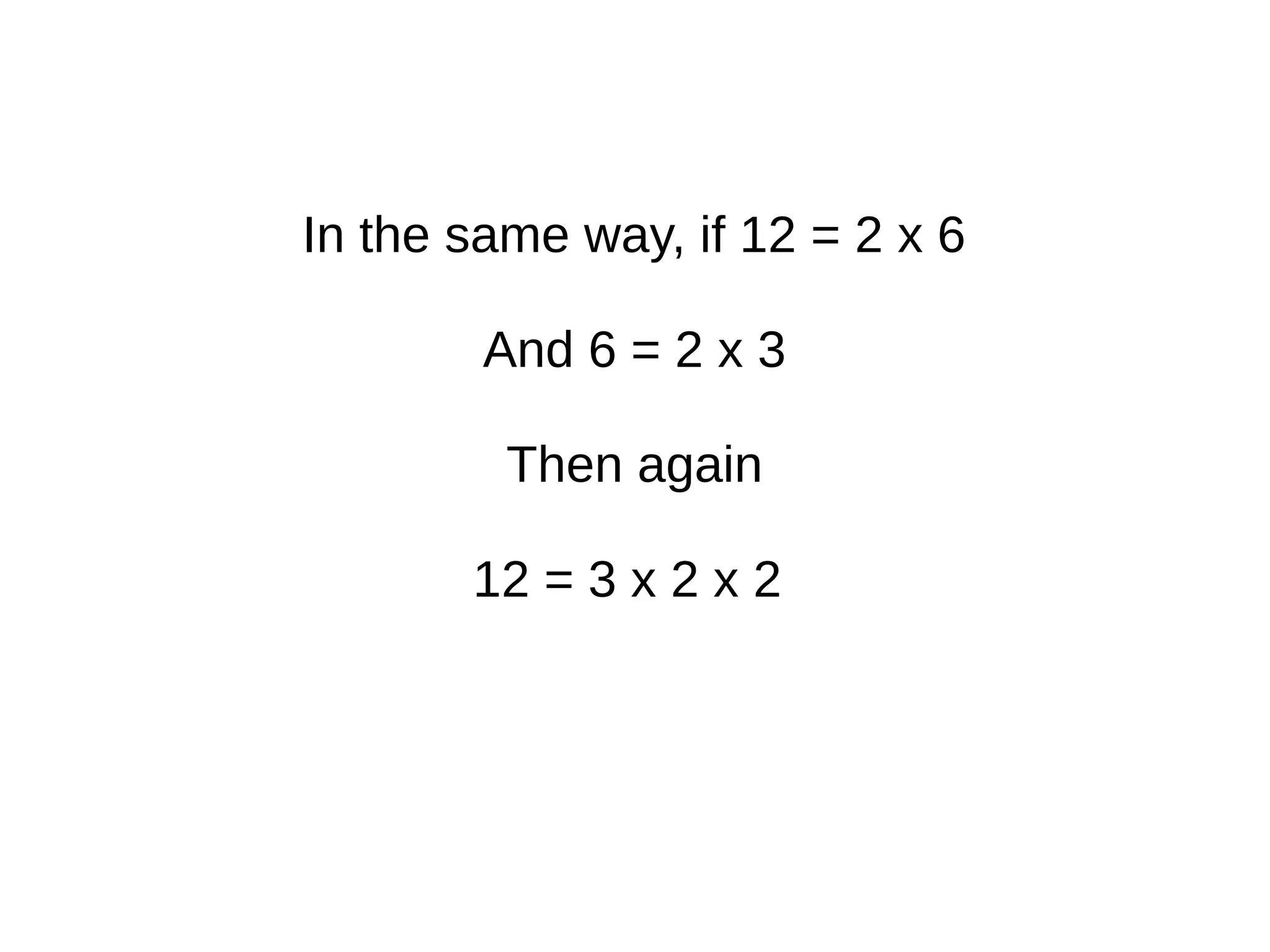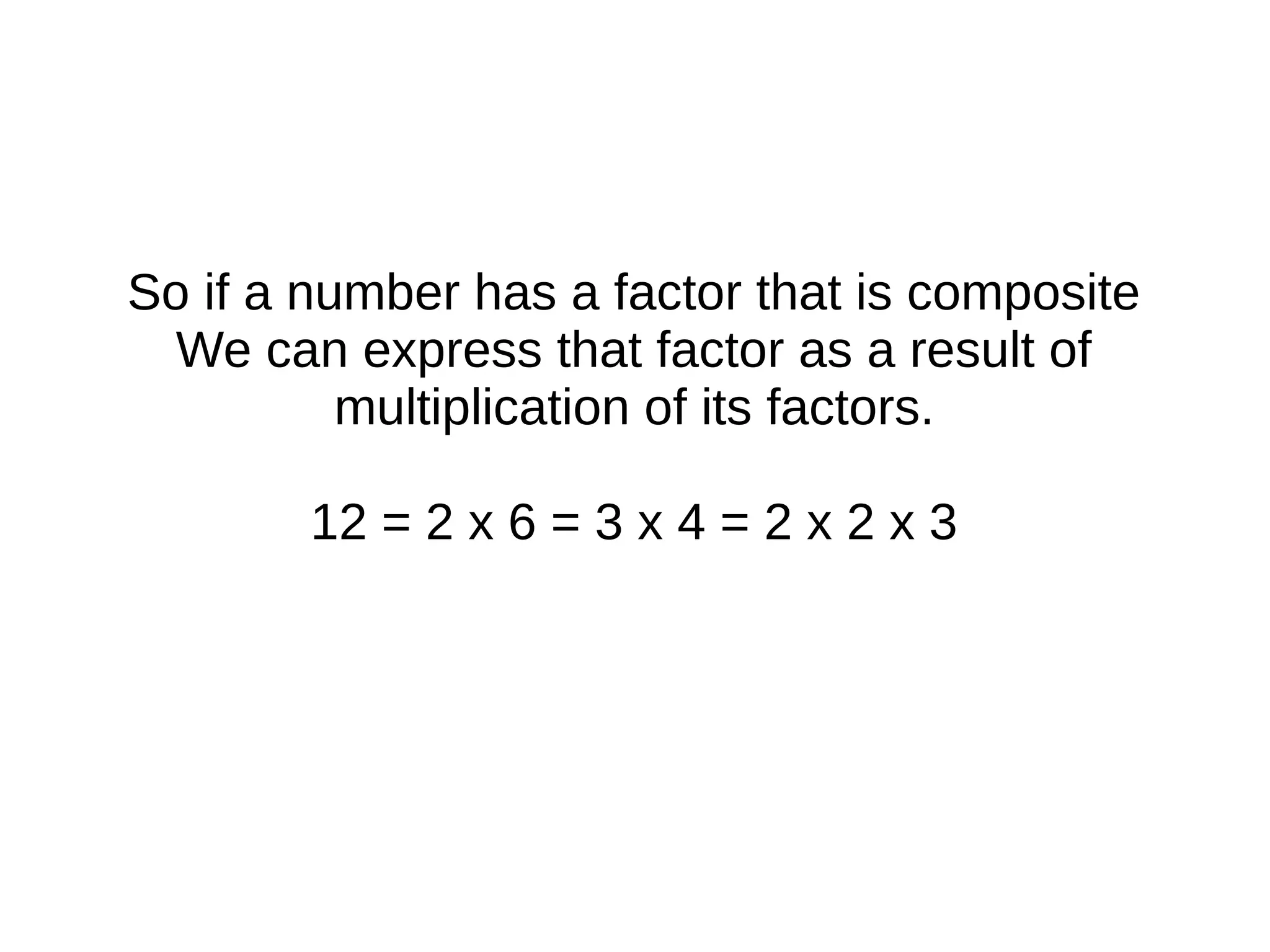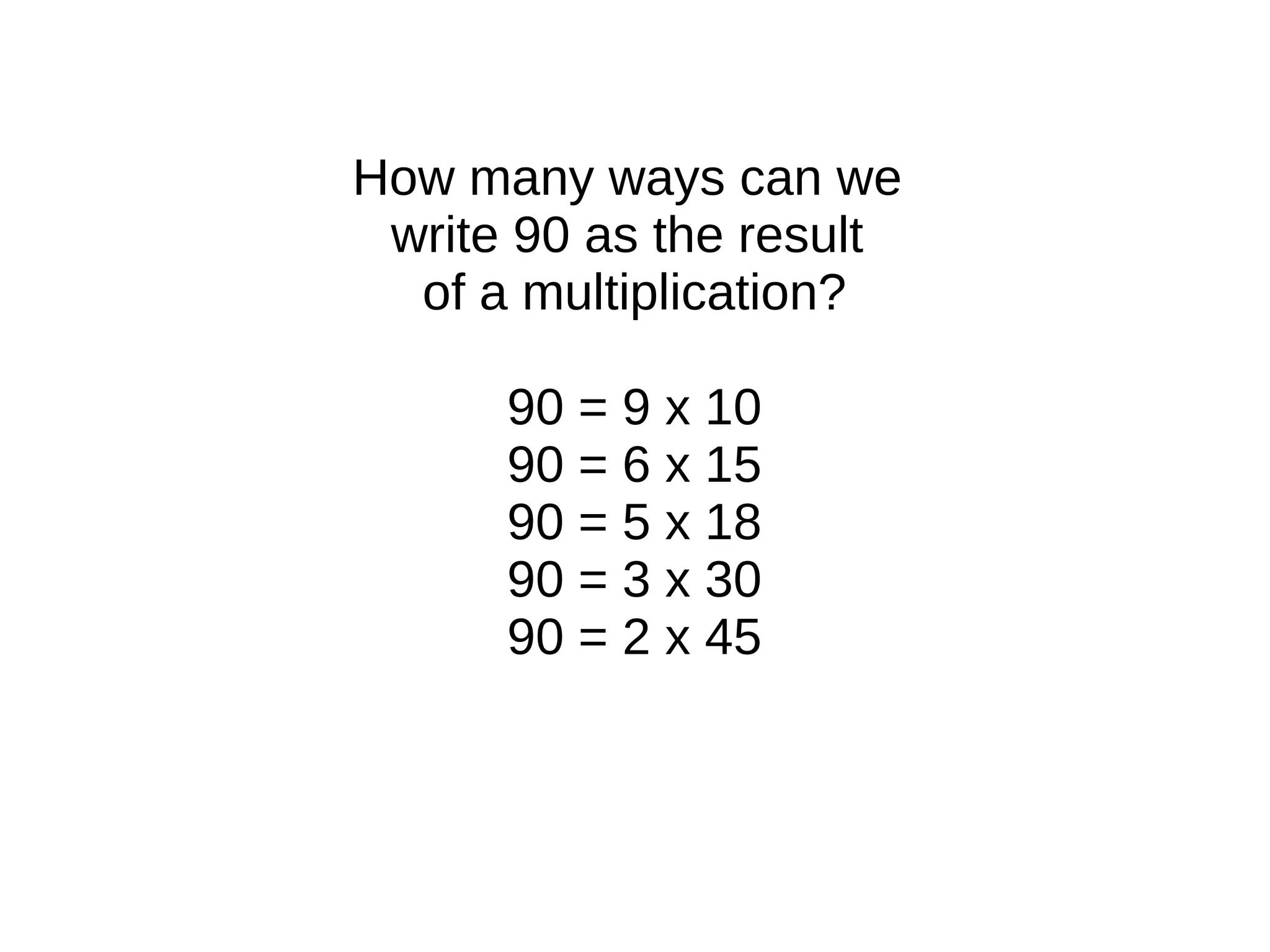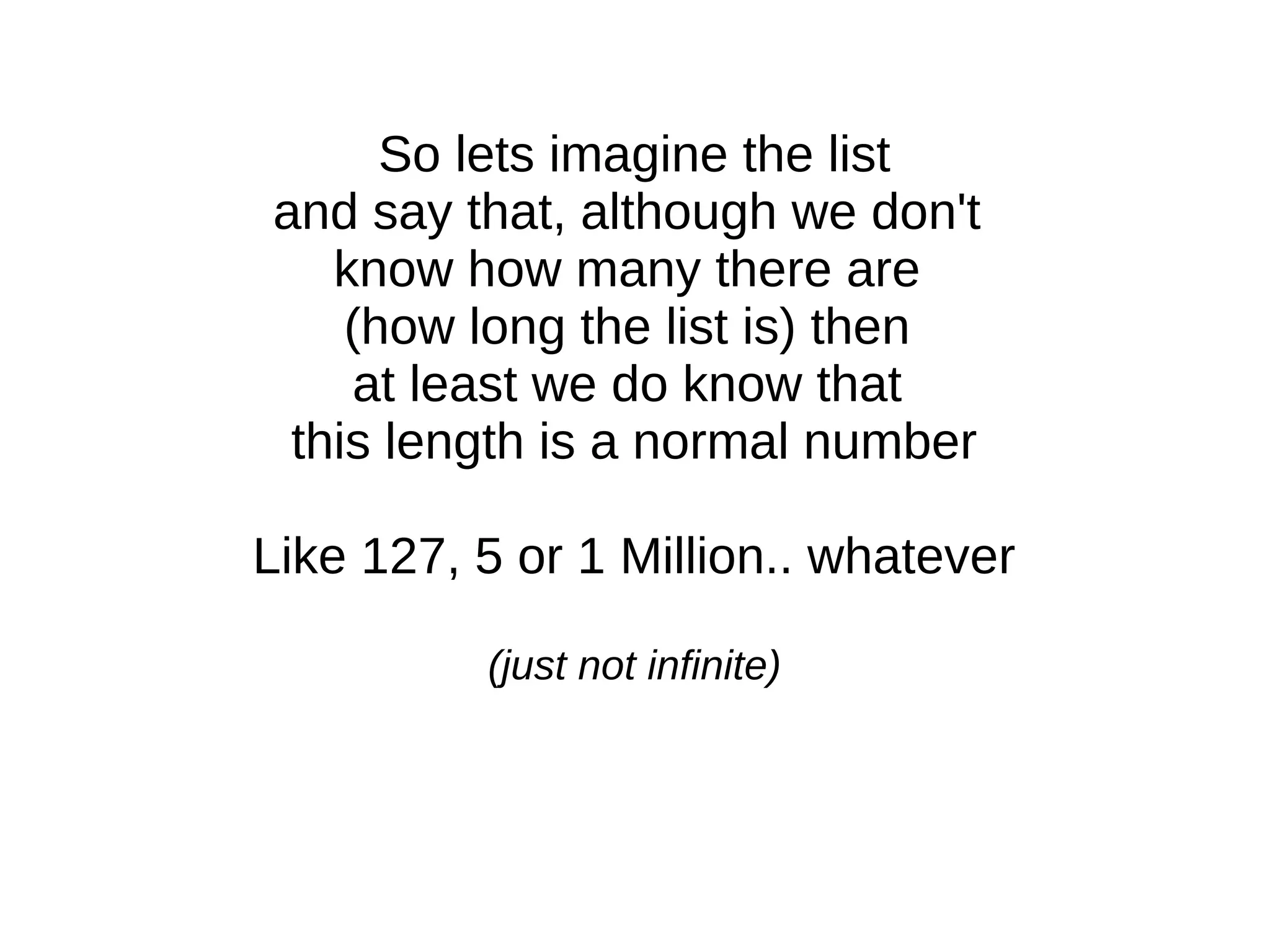The document explains how numbers can be represented as rectangles of dots, introducing the concepts of prime and composite numbers based on their factors. It discusses factorization and the method of breaking composite numbers into their prime constituents. Finally, it presents Euclid's proof demonstrating that there are an infinite number of prime numbers, concluding that a finite list of primes leads to contradictions.