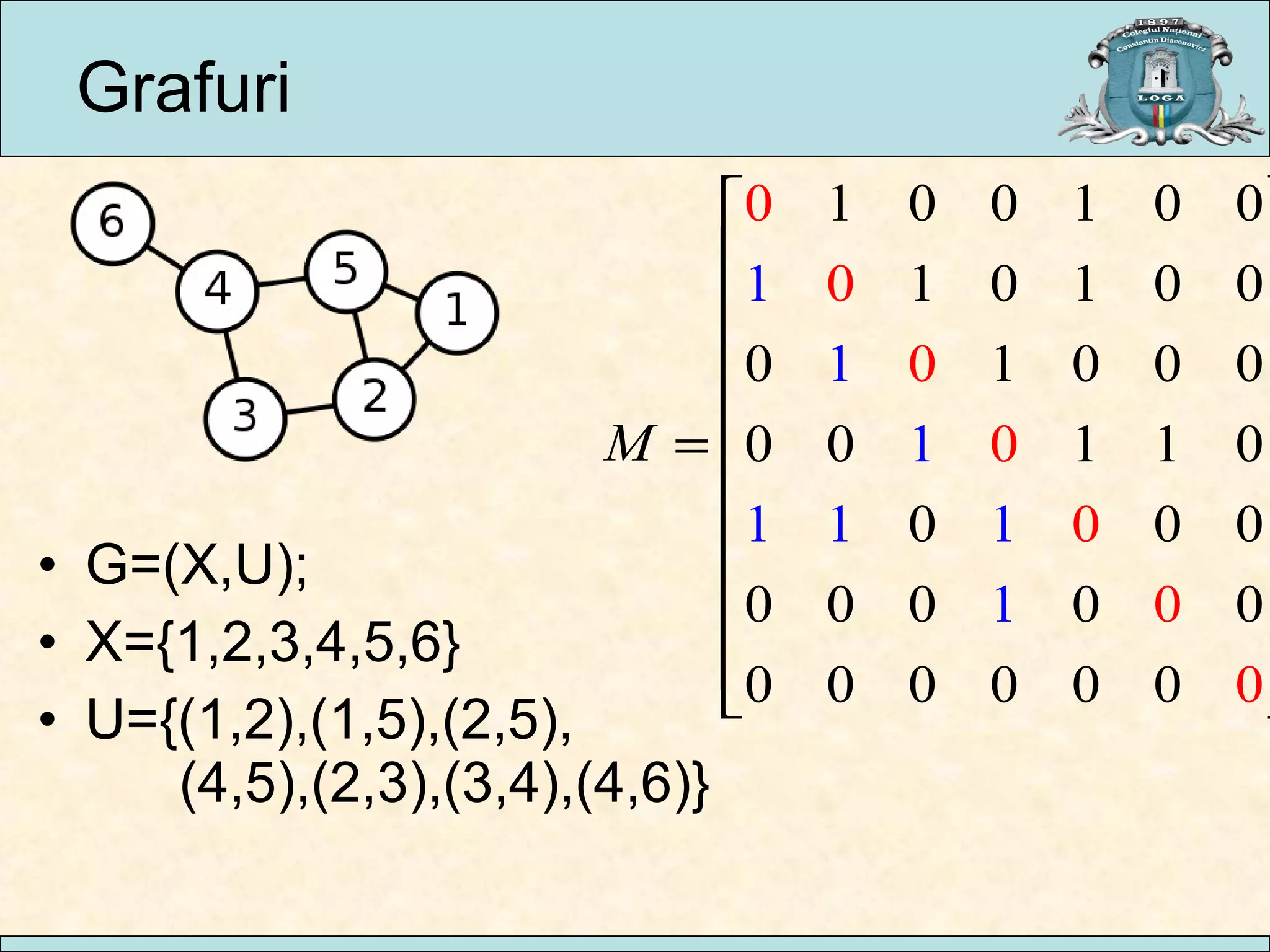
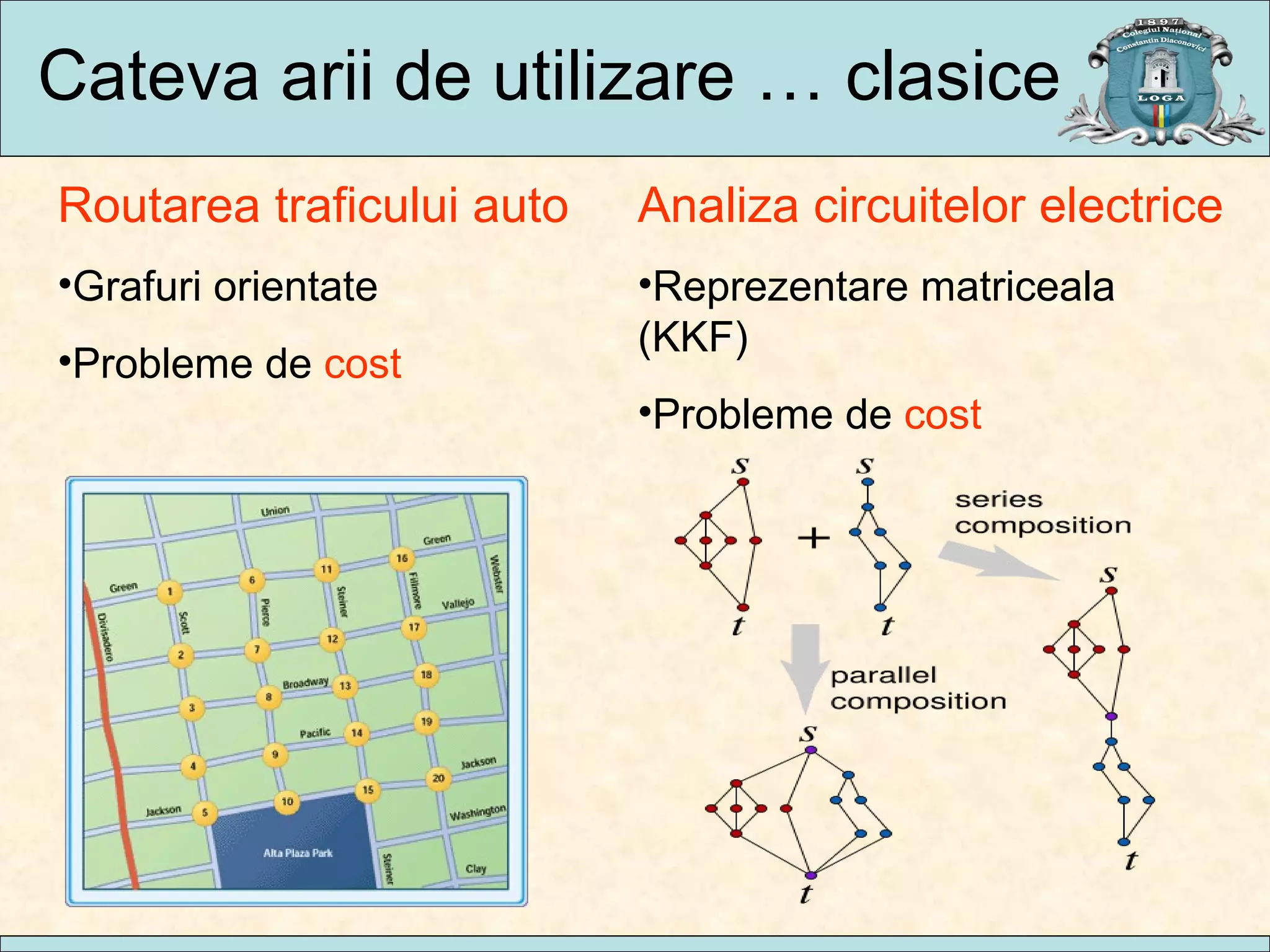
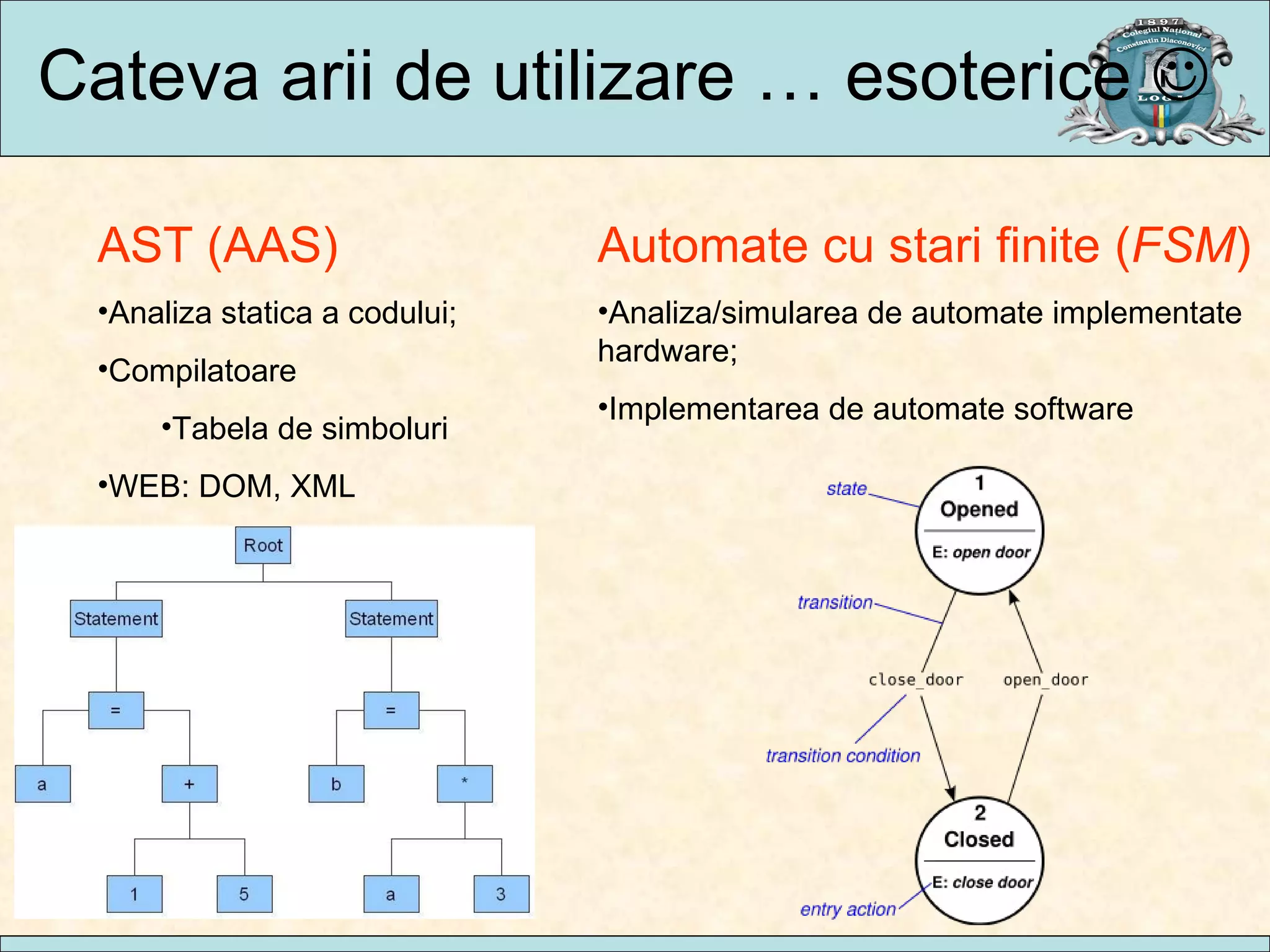
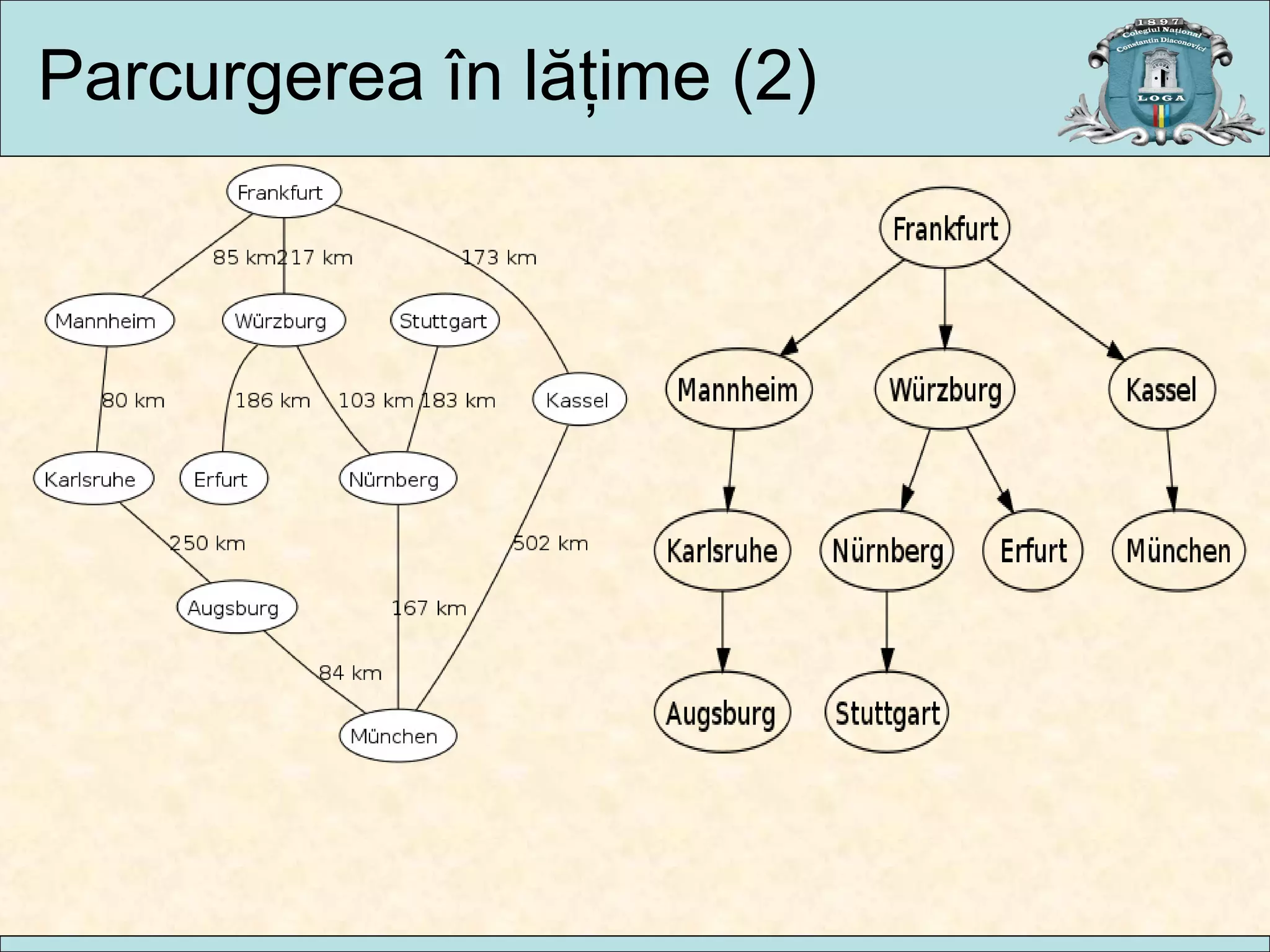
Documentul analizează parcurgerea grafurilor neorientate, prezentând algoritmi precum parcurgerea în lățime și parcurgerea în adâncime, împreună cu aplicații practice în diverse domenii. Se discută despre complexitatea acestor algoritmi și implementarea lor, oferind exemple de utilizare în analiza circuitelor electrice, rutarea traficului și analiza codului. Concluziile indică faptul că traversarea graficelor este esențială pentru accesul la noduri și că diversitatea algoritmilor permite adaptarea la diferite necesități.

1. Dilbert moment 

2. Parcurgerea grafurilor neorientate ing. Alexandru IOVANOVICI februarie 2010 Colegiul Na ţional “C. D. Loga”, Timi şoara

3. Ce vom face ? Scurta recapitulare: grafuri; Cateva domenii de aplicare a grafurilor Mai simple … si mai esoterice. Traversarea grafurilor: Algoritmi; + Implementare Particularitati; Aplicatii

4. Ce veti stii ? Sa parcurgeti toate nodurile unui graf; Sa aplicati prelucrari asupra nodurilor; Sa alegeti intre diferiti algoritmi in functie de necesitati.

5. Grafuri G =(X,U); X={1,2,3,4,5,6} U={(1,2),(1,5),(2,5), (4,5),(2,3),(3,4),(4,6)}

6. Cateva arii de utilizare … clasice Routarea traficului auto Grafuri orientate Probleme de cost Analiza circuitelor electrice Reprezentare matriceala (KKF) Probleme de cost

7. Cateva arii de utilizare … esoterice  AST (AAS) Analiza statica a codului; Compilatoare Tabela de simboluri WEB: DOM, XML Automate cu stari finite ( FSM ) Analiza/simularea de automate implementate hardware; Implementarea de automate software

8. Cateva arii de utilizare … esoterice  Analize de fiabilitate Hardware & software

9. Concluzii ... pana acum Toate aplica ţiile de mai sus necesită accesul la noduri -> traversarea grafurilor

10. Traversarea grafurilor se referă la problema vizitării tuturor nodurilor dintr-un graf, într-o manieră organizată ; Traversarea poate implica vizitarea fiec ărui nod de mai multe ori ; Nu este necesar ă existenţa unui nod de tip radăcina -unica (root-node) Multe metode de traversare ... d intre care două sunt clasice : Parcurgerea in latime (Breath first traversal – BFT ); Parcurgerea in adancime/inaltime (Depth First Traversal – DFT )

11. Parcurgerea în lăţime Se incepe cu un nod ales drept radacina ( start ) şi se viz itează toate nodurile vecine ; Pentru fiecare vecin se vizitea ză vecinii neeploraţi ai acestuia ; Procedura se repetă până ce nu mai rămâne nicinun nod neeplorat. Observaţii : Este un algoritm exhaustiv : parcurge tot graful indiferent de cuno ştiinţele adunate pe parcurs (spre deosebire de unul euristic ). Ordinul de complexitate este O( |X|+|U|) - at ât în timp cât si în spaţiu ; A B C D E F G H

12. Parcurgerea în lăţime (2)

13. Parcurgerea în lăţime (3) Implementare http://www.iovanalex.ro/loga/src/bfs.cpp Pseudocod Adauga nodul de start in coada ; Scoate nodul din coada si aplica procesarea; Daca acest nod este ultimul ce se doreste a fi procesat TERMINA; Altfel adauga in coada succesorii acestui nod, care nu au fost procesati; Daca coada este goala inseamna ca toate nodurile au fost procesate -> TERMINA; Repeta pasul (2) Observatii: Procesul NU este inerent recursiv; Se poate implementa si recursiv; Mecanism de tip coada: FIFO (LILO)

14. Parcurgerea în lăţime (4) Observatii Complexitatea: Complexitatea spatiala este proportionala cu numarul de noduri ≈ O(b d ) – exponential cu adancimea ; Temporal: in cel mai rau caz se exploreaza TOATE nodurile (!!!) - ≈ O(bd) Algoritmul BFS este complet : daca exista o solutie, algoritmul o va gasi intotdeauna. Daca graful este infinit (ca si nr. de noduri) problema se complica 

15. Parcurgerea în lăţime (5) Aplica ţii : Gasirea tuturor nodurilor conectate la un nod; Prelucrari exhaustive ale nodurilor; Diversi algoritmi cu nume de persoane 

16. Aplicatie Se considera graful din figura Sa se precizeze ordinea nodurilor rezultata in urma traversarii BFS ; Se va presupune ca nodurile sunt ordonate alfabetic (daca exista mai multe alternative, nodurile se vor selecta in ordine alfabetica).

17. Parcurgerea în ad âncime Se incepe cu un nod ales drept radacina ( start ) şi se viz itează toate nodurile vecine în adâncimea garfului ; Ajungand la adancimea maxima algoritmul se intoarce pentru a explora o alta cale. Comportament de tip backtracking Observaţii : Este un algoritm exhaustiv : parcurge tot graful indiferent de cuno ştiinţele adunate pe parcurs (spre deosebire de unul euristic ). Ordinul de complexitate este O( |X|+|U|) - at ât în timp cât si în spaţiu ; (!!!) - La fel ca si BFS -> alegerea nu depinde de complexitate; A B C D E F G H

18. Parcurgerea în ad âncime (2) Plecare din A; Se aleg initial nodurile STANGA; DFS= {A,B,D,F,E,C,G} Fara marcarea vizitarii: {A, B, D, F, E, A, B, D, F, E, ………} algorithm dft(x) { visit(x); //prelucrez informatia din nod FOR (isEdge(x,y)) //exista muchie intre (x,y) DO IF notVisited(y) THEN dft(y);//vizitam nodul DONE ROF }

19. Parcurgerea în ad âncime (2) Parcurgere cu scopul ordonarii: Obtinem o reprezentare liniara, ordonata a grafului original; In preordine : ordinea in care au fost vizitate nodurile de algoritmul DFS. Este o reprezentare compacta de prezentare a evolutiei algoritmului. Daca este vb. de o expresie arith., obtinem Notatia Poloneza In postordine : invers decat ordinea de vizitare. Obtinem: RPN (notatia poloneza inversa); Inordine : se aplica pentru arbori (vom reveni). Postordine inversa : utila in analiza fluxurilor de control: IF-THEN-ELSE

20. Parcurgerea în înălţime (3) Implementare http://www.iovanalex.ro/loga/src/dfs.cpp Pseudocod Se adauga nodul de start in stiva ; Repeta Se scoate nodul din stiva (varful); Se prelucreaza acel nod; Se pun in stiva nodurile adiacente nodului curent; Pana cand stiva e vida. Observatii: Procesul ESTE inerent recursiv; Se poate implementa si iterativ; Mecanism de tip stiva: LILO Folosirea cozii in loc de stiva transforma algoritmul in BFS; De cele mai multe ori se apeleaza la recursivitate pentru a exploata stiva interna a sistemului ( stack )

21. Parcurgerea în înălţime (4) Observatii Complexitatea: La fel ca si DFS: O(|X|+|U|) Algoritmi de inteligenta artificiala: arborele solutiilor este fooooarte mare si adanc; Se folosesc algoritmi DFS cu limitarea adancimii; Sau alti algoritmi de cautare: αβ -pruning . Aplica ţii : Ca si la BFS – cautare + prelucrare; Serializare (!!!)

22. Tema (1) Fie graful cu nodurile notate cu literele de la A la M si cu arcele AB, AC, AF, AG, DE, DF, EG, HI, HJ, HK, JK, LM. Sa se reprezinte grafic graful; Sa se determine si sa se scrie matricea de adiacenta; Sa se determine gradul maxim si nodurile corespunzatoare (rezolvare C/C++); Sa se determine s ă se scrie lista nodurilor pentru parcuregerea in latime, cu plecare din A si din C.

23. Bibliografie Robert SEDGEWICK – Algorithms , Addison-Wesley 1983; Thomas H Cormen, Charles E Leiserson, Ronald L Rivest, Clifford Stein (CLR) - Introduction to Algorithms, McGraw-Hill 2 nd . edition, 2001; Robert Sedgewick - Algorithms in Java, Part 5: Graph Algorithms (3rd Edition) , Addison-Wesley Professional; 3 rd . Edition, 2003 Orice manual autorizat; Google 

24. Intrebari … ?