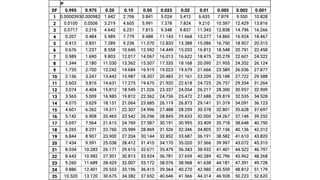
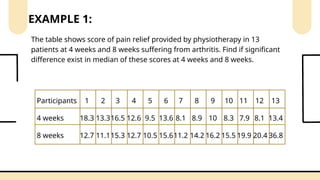
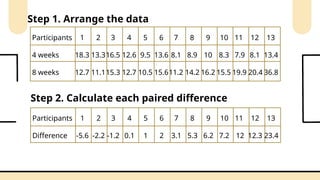
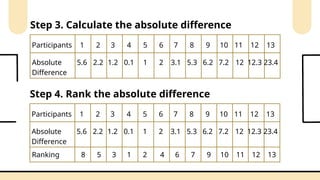
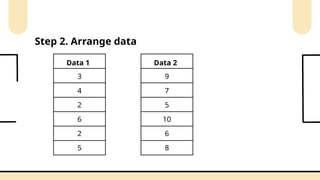
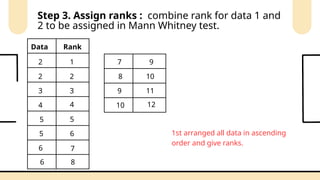
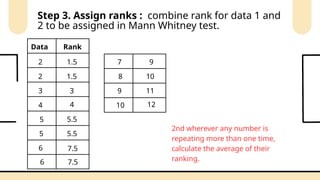
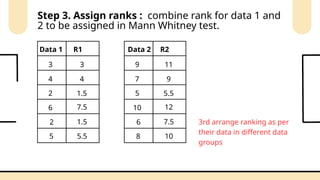
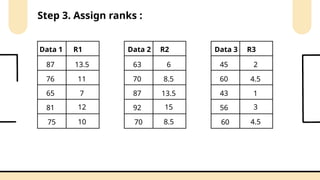
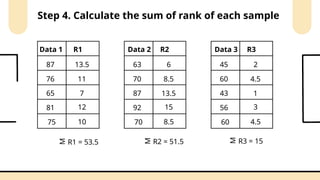
Non-parametric tests are crucial in statistical analysis as they provide a robust alternative to parametric tests when the assumptions of the latter are not met. They are particularly useful when dealing with ordinal data, data that is not normally distributed, or when the sample size is too small to assume normality.

1. NON-PARAMETRIC
TEST
Presented by
Rexiel Llene Pascua
Xhyra Villanueva
Riotes Richinel Raful
Shellie Heart Rafol

2. INTRODUCTION
(Something that decides or limits the way in which something can be done)
PARAMETER
Fixed Parameter
Parametric Statistics
Parametric Test
No fixed Parameter
Non-Parametric
Statistics
Non-Parametric Test

3. Parametric Test Non-Parametric Test
Parameter
Information about
population and parameter is
known
Information about
population and parameter is
known
Assumptions Assumptions are made No assumptions are made
Value for central
tendency Mean Median
Probability Distribution Normal Distribution Arbitrary
Distribution
Power More Powerful Less Powerful
Applicable for Variables Variables & Attributes
Null Hypothesis
Made on parameters of
population distribution
Free from parameters
DIFFERENCE BETWEEN PARAMETRIC AND NON-
PARAMETRIC TEST

4. Parametric Test Non-Parametric Test
Used for Ratio or interval data Nonminal or Ordinal data
Independent
measures (2 groups)
Intedendent measure
t-test Mann Whitney U test
One way independent
measure ANOVA
Kruskal Wallis test
Repeated measures (2
conditions)
Matched pair t-test Arbitrary
Distribution
Independent
measures (>2 groups)

5. • Non - parametric test also known as distribution free test.
• They DO NOT ASSUME that the outcome id approximately
normally distributed
• Situations in which outcome does not follow normal
distribution
NON-PARAMETRIC TESTS
1. When the outcome is an ordinal variable or Rank.
2. When there are definite outlier.
3. When the outcome has clear limit of detection.

6. 1.Mann Whitney U test
2.Kruskal Wallis test
3.Wilcoxon signed rank test
COMMONLY USED NON-
PARAMETRIC TEST

7. MANN WHITNEY
U TEST

8. With the help of Mann Whitney U test, find of significant differences exist
between the score of Treatment A and Treatment B.
EXAMPLE 1:
Treatment A
Treatment B
3, 4, 2, 6, 2, 5
9, 7, 5, 10, 6, 8

9. 1. Generate the hypothesis (Null & Alternative)
2. Arrange data
3. Assign ranks
4. Determine the sum of rank of each sample
5. Calculate U (test) for each sample
6. Take the smaller U (test) value
7. Compare smaller U (test) value with U (Critical) to
accept/reject null hypothesis.
8. Interpret
STEPS TO BE FOLLOWED:

10. Null hypothesis = There is no diference between Treatment A
and Treatment B.
Alternative hypothesis = There is significant difference
between Treatment A and Treatment B.
Step 1. Generate the hypothesis (Null &
Alternative)

11. Step 2. Arrange data
Data 1
3
4
2
6
2
5
Data 2
9
7
5
10
6
8

12. 1st arranged all data in ascending
order and give ranks.
Data
3
4
2
6
2
5
9
7
5
10
6
8
Rank
1
2
3
4
5
6
7
8
9
10
11
12
Step 3. Assign ranks : combine rank for data 1 and
2 to be assigned in Mann Whitney test.

13. 2nd wherever any number is
repeating more than one time,
calculate the average of their
ranking.
Data
3
4
2
6
2
5
9
7
5
10
6
8
Rank
1.5
1.5
3
4
5.5
5.5
7.5
7.5
9
10
11
12
Step 3. Assign ranks : combine rank for data 1 and
2 to be assigned in Mann Whitney test.

14. 3rd arrange ranking as per
their data in different data
groups
Data 1
2
6
4
3
2
5
R1
3
4
1.5
7.5
1.5
5.5
Step 3. Assign ranks : combine rank for data 1 and
2 to be assigned in Mann Whitney test.
Data 2
5
10
7
9
6
8
R2
11
9
5.5
12
7.5
10

15. Data 1
2
6
4
3
2
5
R1
3
4
1.5
7.5
1.5
5.5
Step 4. Calculate the sum of ranks of each sample
Data 2
5
10
7
9
6
8
R2
11
9
5.5
12
7.5
10
M
R1 = 23
M
R2 = 55

16. Step 5. Calculate U (test) for each Sample
U (test) = Rank sum - n (n + 1)
2
For Treatment A = 23 - 6(6+1)/2 =
2.0
For Treatment B = 55 - 6(6+1)/2
= 34.0
Step 6. Take the smaller U (test) value
Smaller U (test) value is 2.0 for Treatment A

18. Step 7. Compare smaller U (test) value with U
(Critical) to accept/reject hypothesis
U (test) = 2
U (Critical) = 6
U (test) < U (Critical)
Step 8. Interpretation if..
H (test) < H (Critical), reject null hypotheis
H (test) > H (Critical), accept null hypotheis
Null hypothesis rejected and alternative hypothesis is accepted
“There is signifact difference between Treatment A and Treatment B”

19. KRUSKAL
WALLIS TEST

20. 15 patients having complaint of tooth decay were randomly assigned to 3
groups of each. One group (group A) was given no treatment. Second
group (group B) was given drug A and third group (group C) was given
drug B. At the end of six weeks, the extent of tooth decay was eveluated
as % of tooth decay. We wish to know if there is a difference among three
groups.
EXAMPLE 1:
Drug A
Control Group 87
Drug B
63
45
81
76 65 75
70
60
87
43
92 70
60
56

21. 1. Generate the hypothesis (Null & Alternative)
2. Arrange data
3. Assign ranks
4. Determine the sum of rank of each sample
5. Calculate H (test)
6. Calculate degree of freedom
7. Compare H (test) value with H (Critical) to
accept/reject null hypothesis.
8. Interpret
STEPS TO BE FOLLOWED:

22. Null hypothesis = There is no difference in extent of tooth
decay among three groups.
Alternative hypothesis = There is a difference in extent of tooth
decay among three groups.
Step 1. Generate the hypothesis (Null &
Alternative)

23. Step 2. Arrange data
Data 1
87
76
65
81
75
Data 1 Data 1
63 45
70
87
92
70
60
43
56
60

24. Data 1
65
81
76
87
75
R1
13.5
11
7
12
10
Step 3. Assign ranks :
Data 2
87
92
70
63
70
R2
6
8.5
13.5
15
8.5
Data 3
43
56
60
45
60
R3
2
4.5
1
3
4.5

25. Data 1
65
81
76
87
75
R1
13.5
11
7
12
10
Step 4. Calculate the sum of rank of each sample
Data 2
87
92
70
63
70
R2
6
8.5
13.5
15
8.5
Data 3
43
56
60
45
60
R3
2
4.5
1
3
4.5
M
R1 = 53.5
M
R2 = 51.5
M
R3 = 15

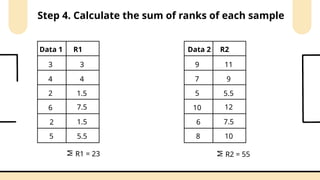
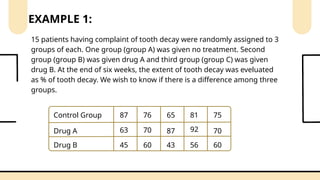
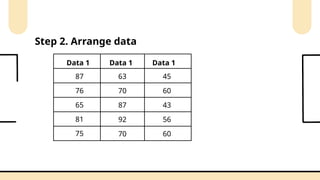
26. Step 5. Calculate H (test)
(12)
N (N=1)
H
=
[
M
(
M
R) 2]
n
- 3(N + 1)
N = Total # of participants
n = # of participant in one
group
(12)
15(15 + 1)
H
= 5
- 3(15 + 1)
(53.5)2
+
5
(51.5)2
+
5
(15)2
H (test) = 9.39

27. K (No. of groups) - 1 = 3 -1 = 2
Step 6. Calculate the degre of freedom
Step 7. Compare H (test) value with H (Critical) by
using chi-square table to accept/reject null
hypothesis
a = 0. 05
H(test)
H(Critical)
5.991 9.39 H(test) > H(Critical)

29. H (test) > H (Critical), reject the null hypothesis
H (test) < H (Critical), accept the null hypothesis
Step 8. Interpretation
“There is a difference in extent of tooth decay among three groups.”

30. WILCOXON
SIGNED RANK
TEST

31. • Also called the Wocoxon matched pairs test or the
Wilcoxon signed rank test.
• Appropriate for a repeated measure design where the
same subjects are evaluated under two different
conditions.
• For example, measurements taken every 15 min after
dosing for 2 hrs, each animal will be sampled once for base
line, and 8 times for treatment resulting in 8 comparisons.
However, these 8 groups are not independent as they are
all obtained from the same set of animals after the same
treatment.
WILCOXON SIGNED RANK
TEST

32. The table shows score of pain relief provided by physiotherapy in 13
patients at 4 weeks and 8 weeks suffering from arthritis. Find if significant
difference exist in median of these scores at 4 weeks and 8 weeks.
EXAMPLE 1:
Participants
4 weeks
8 weeks
1 2 3 4 5 6 7 8 9 10 11 12 13
18.3
12.7
13.3
11.1
16.5
15.3
12.6
12.7
9.5
10.5
13.6
15.6
8.1
11.2
8.9
14.2
10
16.2
8.3
15.5
7.9
19.9
8.1
20.4
13.4
36.8

33. Step 1. Arrange the data
Participants
4 weeks
8 weeks
1 2 3 4 5 6 7 8 9 10 11 12 13
18.3
12.7
13.3
11.1
16.5
15.3
12.6
12.7
9.5
10.5
13.6
15.6
8.1
11.2
8.9
14.2
10
16.2
8.3
15.5
7.9
19.9
8.1
20.4
13.4
36.8
Step 2. Calculate each paired difference
Participants
Difference
1 2 3 4 5 6 7 8 9 10 11 12 13
-5.6 -2.2 -1.2 0.1 1 2 3.1 5.3 6.2 7.2 12 12.3 23.4

34. Step 3. Calculate the absolute difference
Participants
Absolute
Difference
1 2 3 4 5 6 7 8 9 10 11 12 13
5.6 2.2 1.2 0.1 1 2 3.1 5.3 6.2 7.2 12 12.3 23.4
Step 4. Rank the absolute difference
Participants
Absolute
Difference
1 2 3 4 5 6 7 8 9 10 11 12 13
5.6 2.2 1.2 0.1 1 2 3.1 5.3 6.2 7.2 12 12.3 23.4
Ranking 1 2
3 4
5 6 7
8 9 10 11 12 13

35. Step 5. Calculate rank sum of positive value (T+)
and negative value (T-)
T(-) = 8 + 5 + 3 = 16
T(+) = 1 + 2 + 4 + 6 + 7 + 9 + 10 + 11 + 12 + 13 = 75
Step 6. Smaller T value will be W (test)
W (test) = 16
Step 7. Find out the W (Critical) value by using
wilcoxan signed rank test table
W (Critical) = 17

37. If W (test) < W (Critical), reject the null hypothesis
If W (test) > W (Critical), accept the null hypothesis
Step 8. Interpretation
“There is a significant difference between the median score of pain
reliefat hour and 8 hour duration”
W (test) < W (Critical)

38. Z test =
Z test statistics
T - T
SE
_
T = T (max)
T = 75
T = T (max) + T (min) / 2
_
T = 75 + 16 / 2
_
T = 45.5
_
SE = n (n + 1) (2n + 1)
24
SE = 13 (13 + 1) (2 (13) + 1)
24
SE = 14.30

39. Z test =
Z test statistics
T - T
SE
_
Z test =
75 - 45.5
14. 30
Z test = 2.06
If Z test is > 1.96 at 5% significance, reject the null hypothesis
If Z test is < 1.96 at 5% significance, accept the null hypothesis
In our study Z (test) is 2.06 which is > 1.96 thus null
hypothesis will be rejected.

40. • When parametric tests are not satisfied.
• When testing the hypothesis, it does not have any
distribution.
• For quick data analysis
• When unscaled data is available.
APPLICATIONS OF NON-
PARAMETRIC TEST

41. • Easily understandable
• Short calculations (weh?)
• Assumption of distribution is not required
• Applicable to al types of data
ADVANTAGES OF ON-
PARAMETRIC TEST

42. • Less efficient as compared to parametric test
• The results may or may not provide an accurate answer
because they are distribution free.
DISADVANTAGES OF ON-
PARAMETRIC TEST

43. THANK YOU
OKEY NA 2...
Made by Rexiel Llene Pascua CTTRO for Content