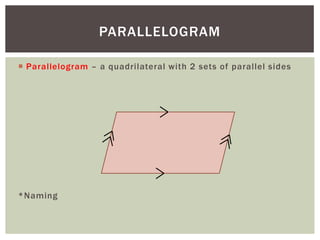
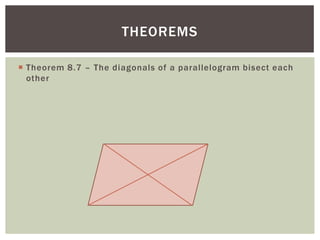
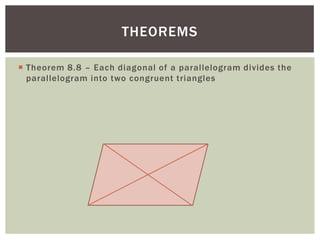
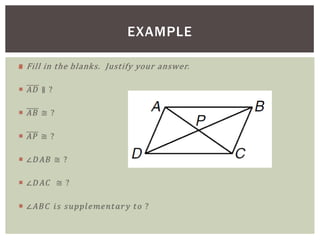
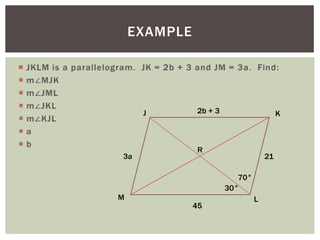
The document discusses properties of parallelograms. It defines a parallelogram as a quadrilateral with two pairs of parallel sides. The key properties are that opposite angles are congruent, opposite sides are congruent, and consecutive interior angles are supplementary. The diagonals of a parallelogram bisect each other and divide the parallelogram into two congruent triangles. Examples and a homework worksheet are provided to help students practice applying these properties.

1. SECTION 8.2 Parallelograms

2. PARALLELOGRAMS
 How can I recognize a parallelogram using the sides and
angles?
 How do I apply the properties of the diagonals of
parallelograms?

3. PARALLELOGRAM
 Parallelogram – a quadrilateral with 2 sets of parallel sides
*Naming

4. PROPERTIES (THEOREMS)
1. Opposite angles are congruent
2. Opposite sides are congruent
3. Consecutive interior angles are supplementary
4. If 1 angle is right, then all angles are right

5. THEOREMS
 Theorem 8.7 – The diagonals of a parallelogram bisect each
other

6. THEOREMS
 Theorem 8.8 – Each diagonal of a parallelogram divides the
parallelogram into two congruent triangles

7. EXAMPLE


8. EXAMPLE

J 2b + 3 K
R
3a 21
70°
30°
M L
45

9. EXAMPLES
 What are the coordinates of the intersection of the diagonals
of parallelogram MNPR, with vertices
M(–3, 0), N(–1 , 3), P(5, 4), and R(3, 1)?

10. HOMEWORK
 Worksheet

11. LESSON PLAN
 Intro
 The first quadrilateral we will discuss is the parallelogram
 Standards- 8.2 (Power)
 Supplies – slides, whiteboard, handouts,
 Timing - 1 day 1 review day and a quiz
 Essential Questions- slide 2
 Input – slides 3-6
 Guided Practice – slides 7-9
 Independent Practice – Worksheet