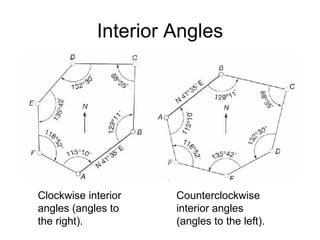
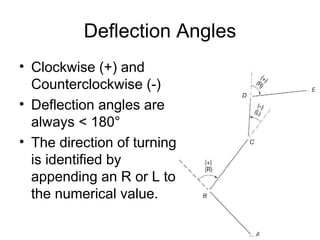
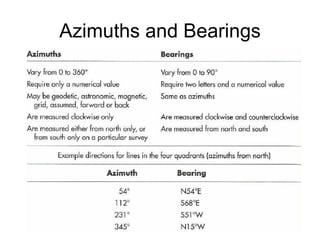
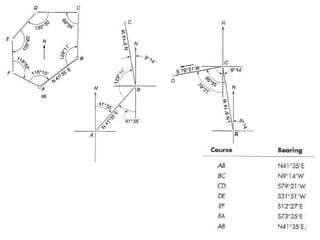
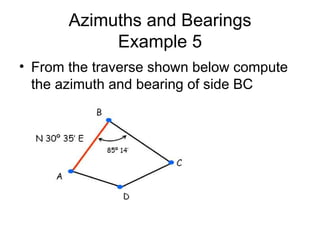
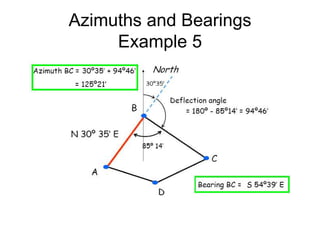
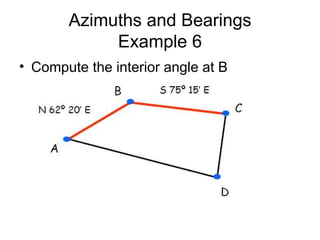
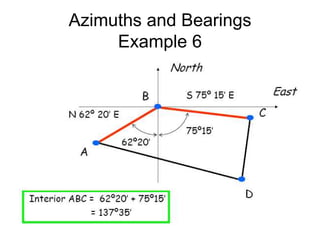
This document provides a comprehensive overview of surveying techniques, focusing on the measurement of angles, azimuths, and bearings. It details various types of angles used in surveying, including interior, exterior, and deflection angles, as well as the differences between azimuths and bearings as systems for designating directions. The document also describes the units of measurement and computation methods used in both the sexagesimal and centesimal systems.