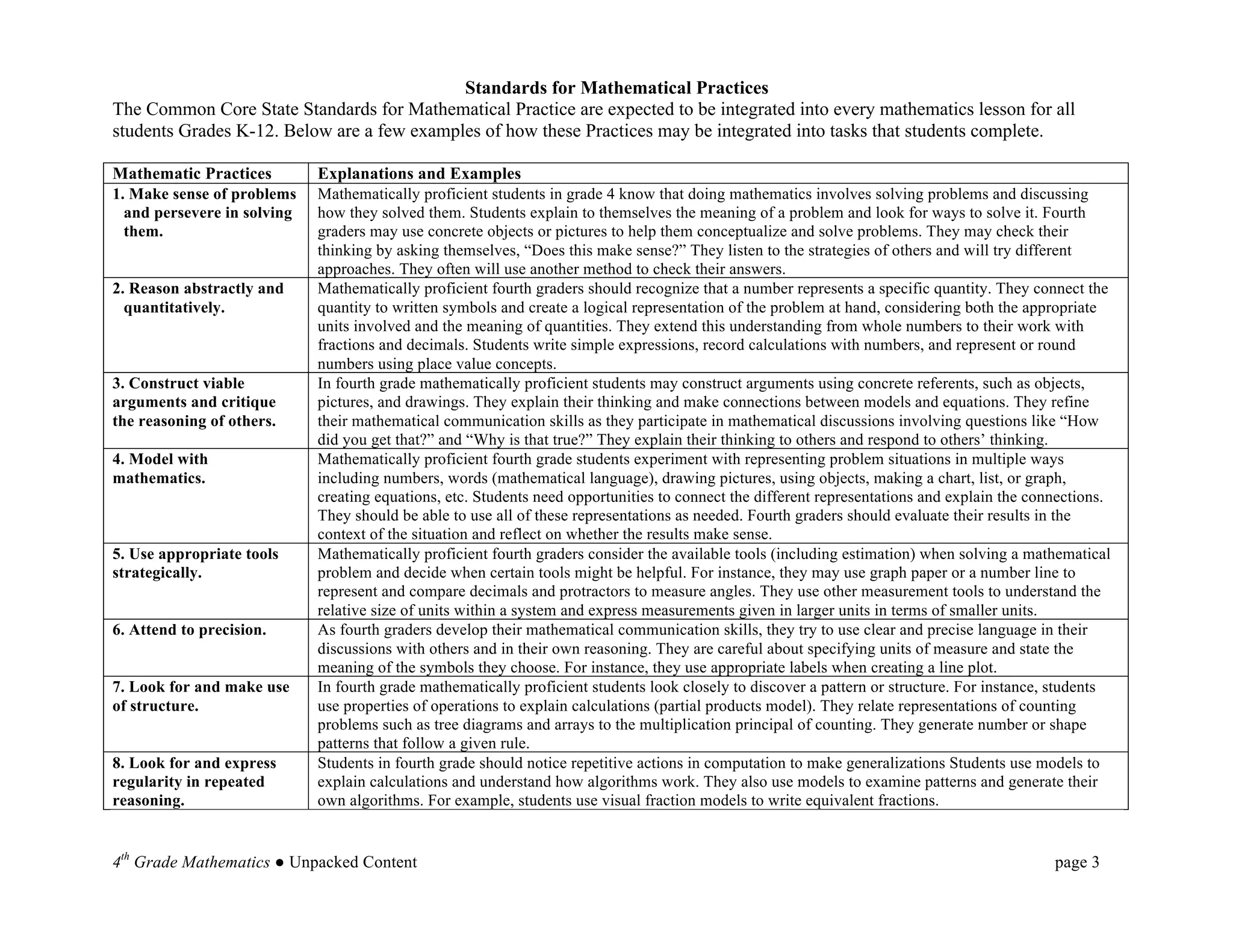
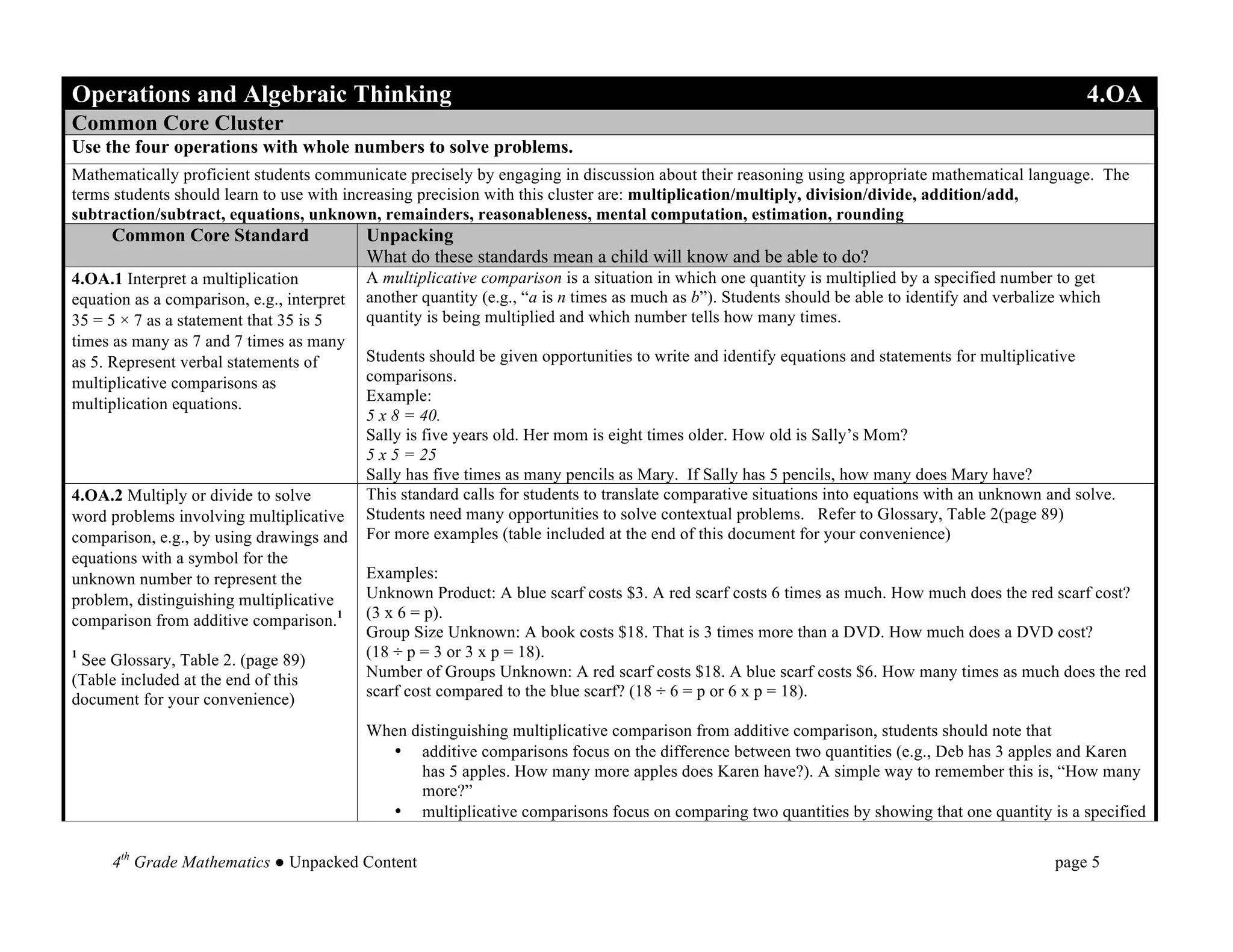
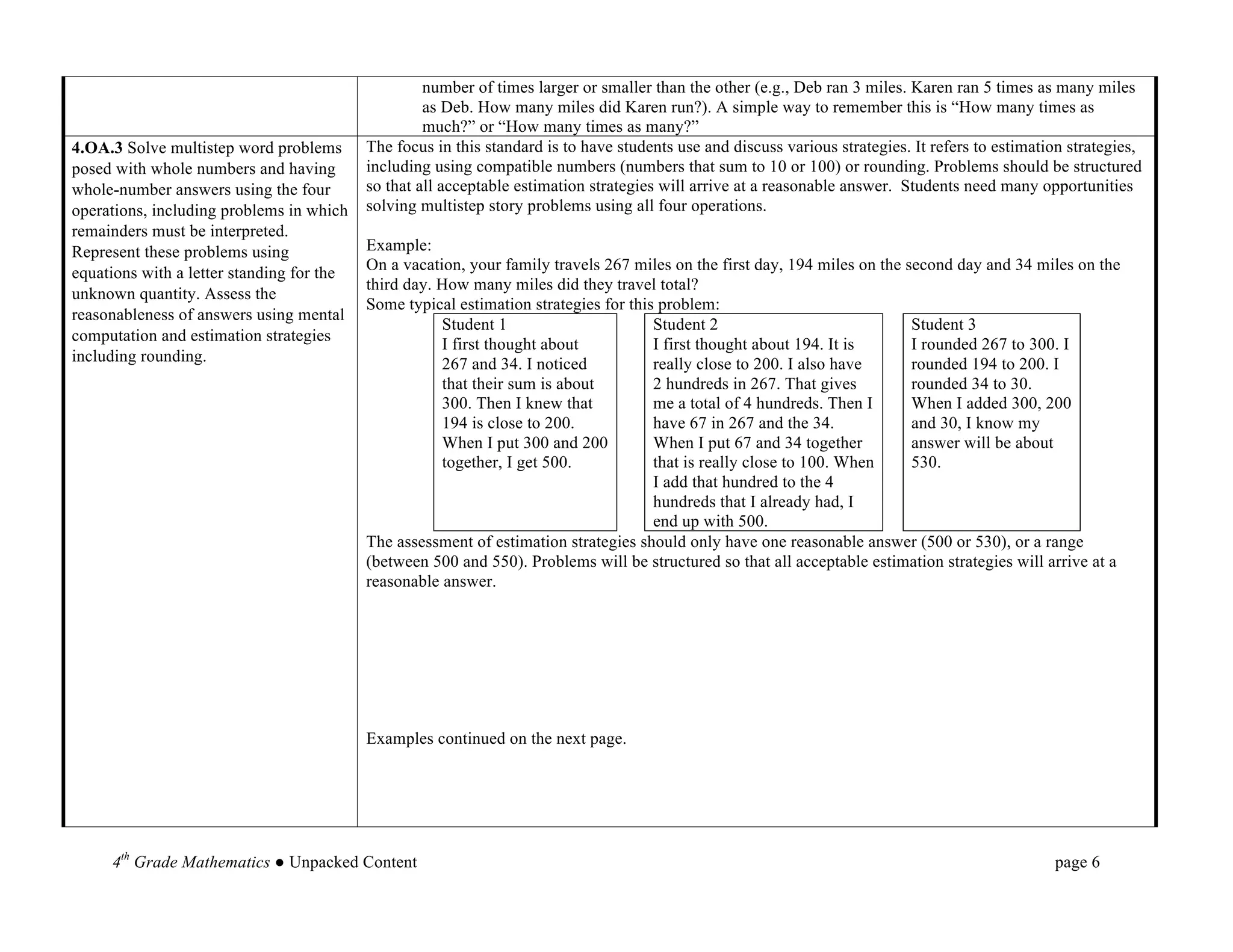
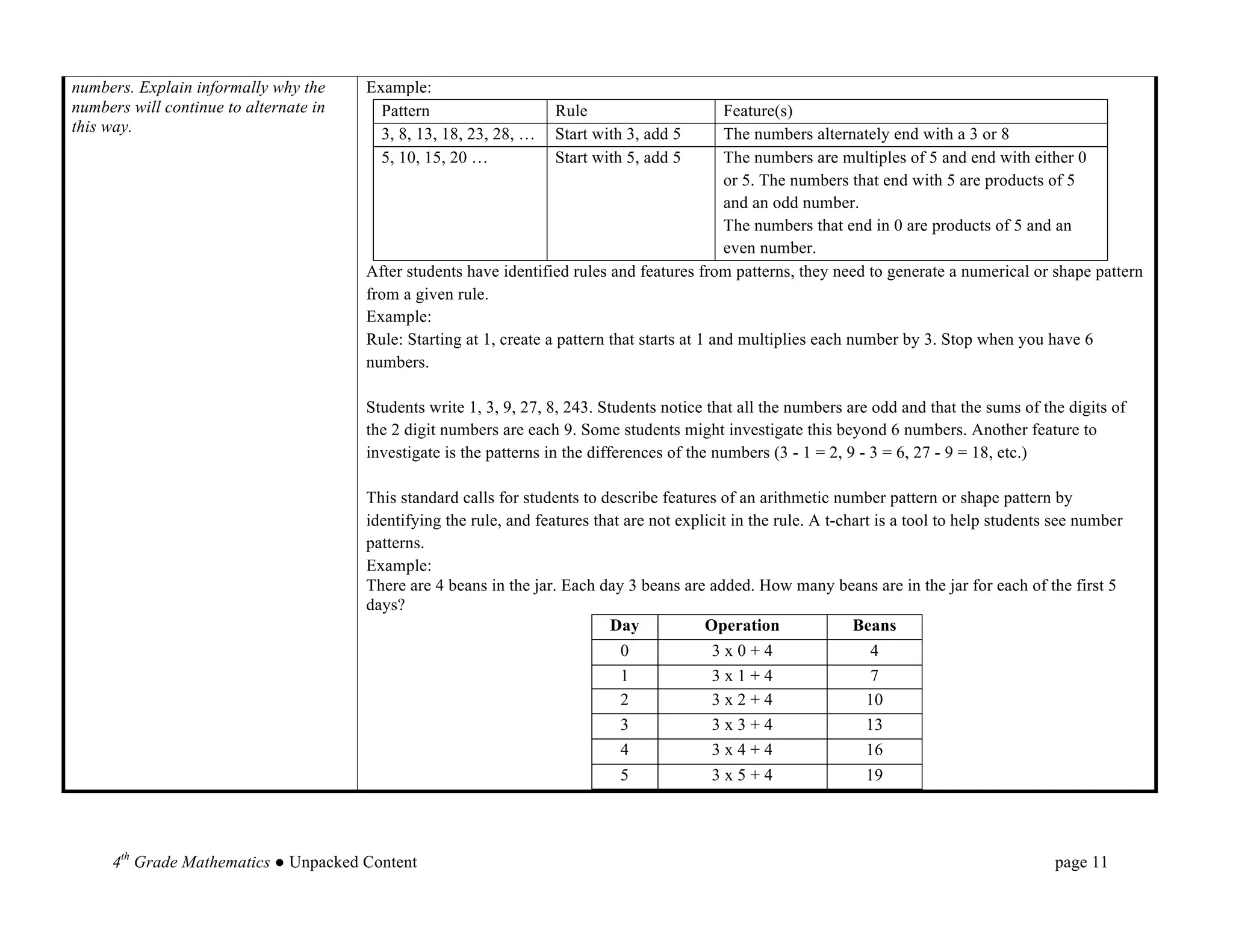
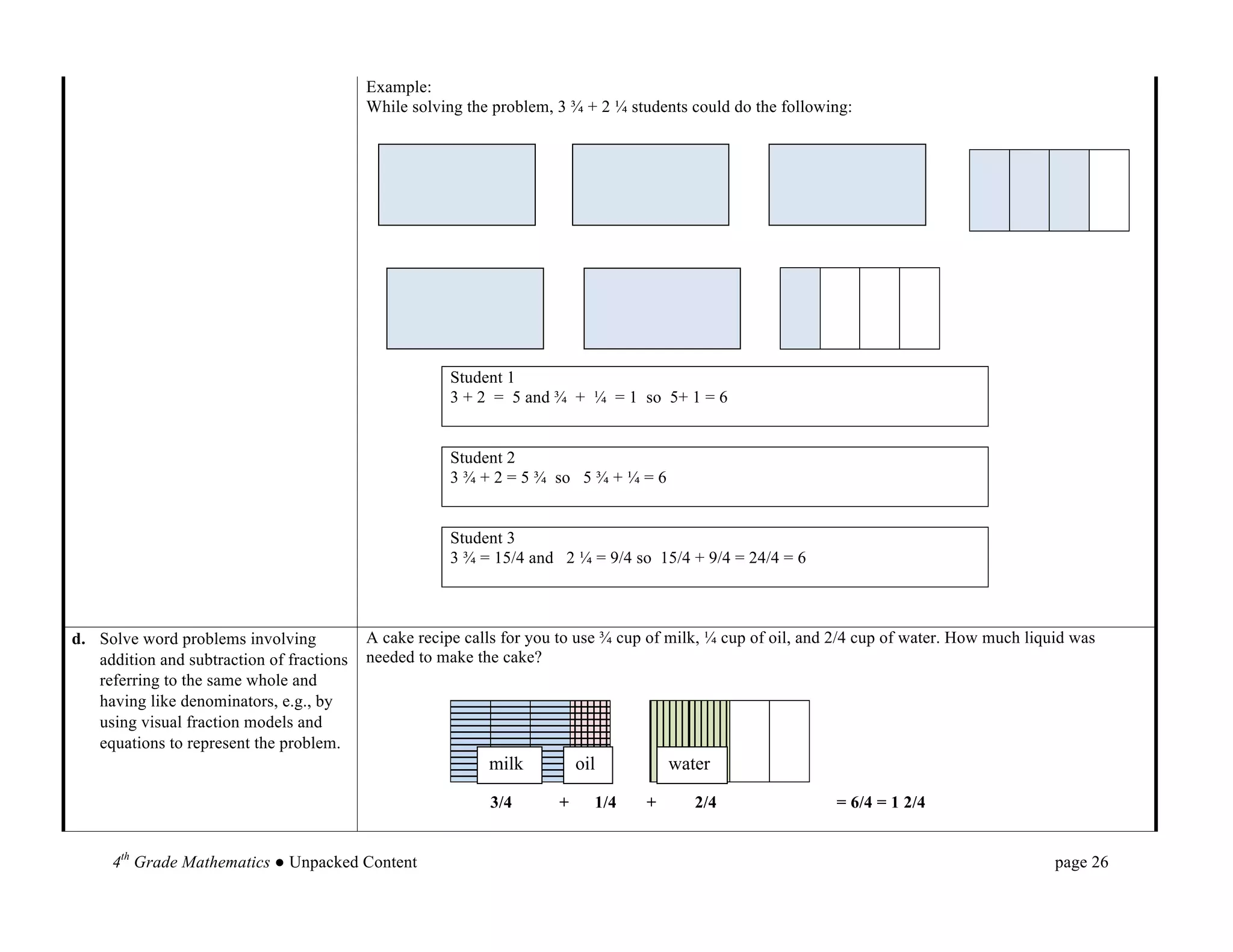
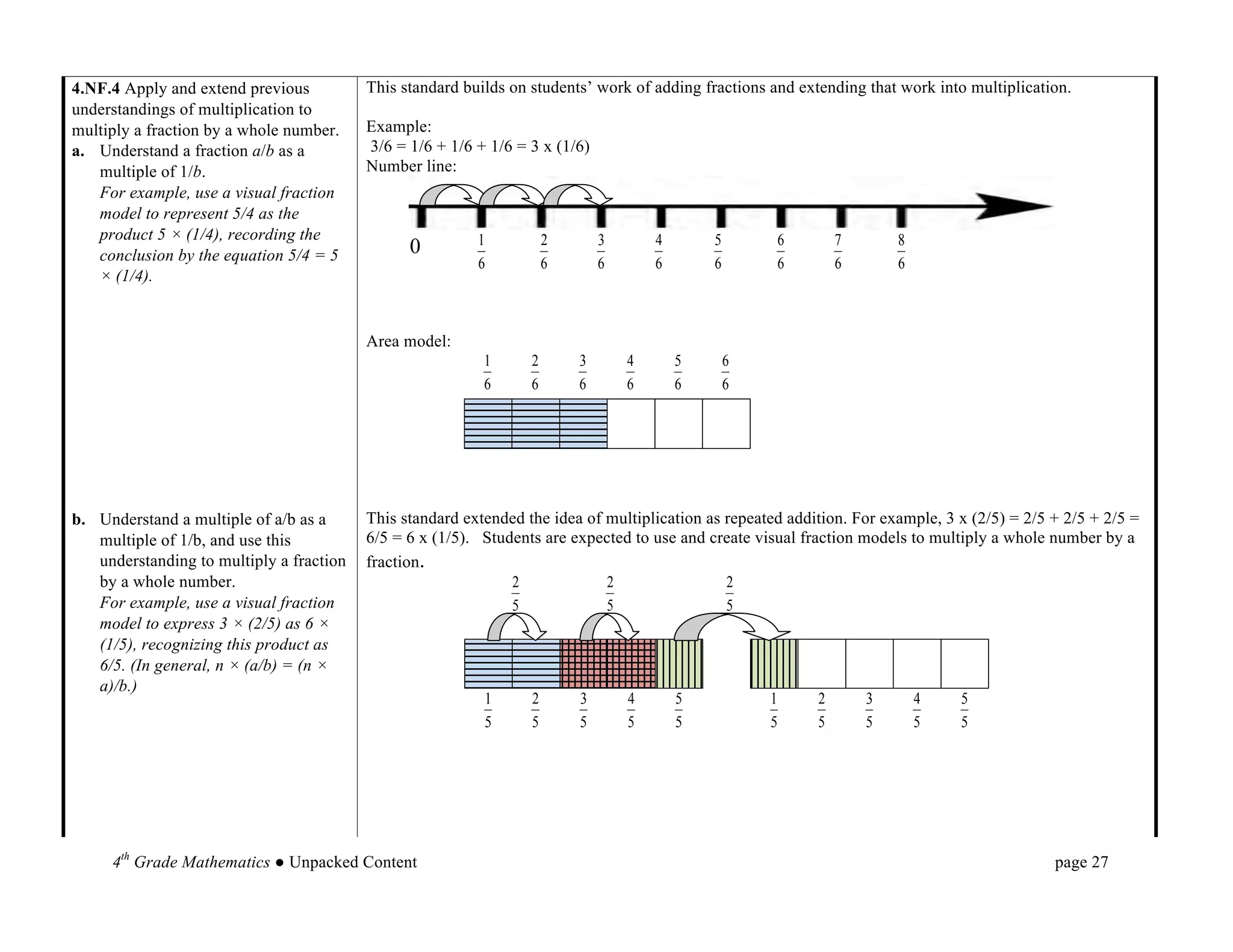
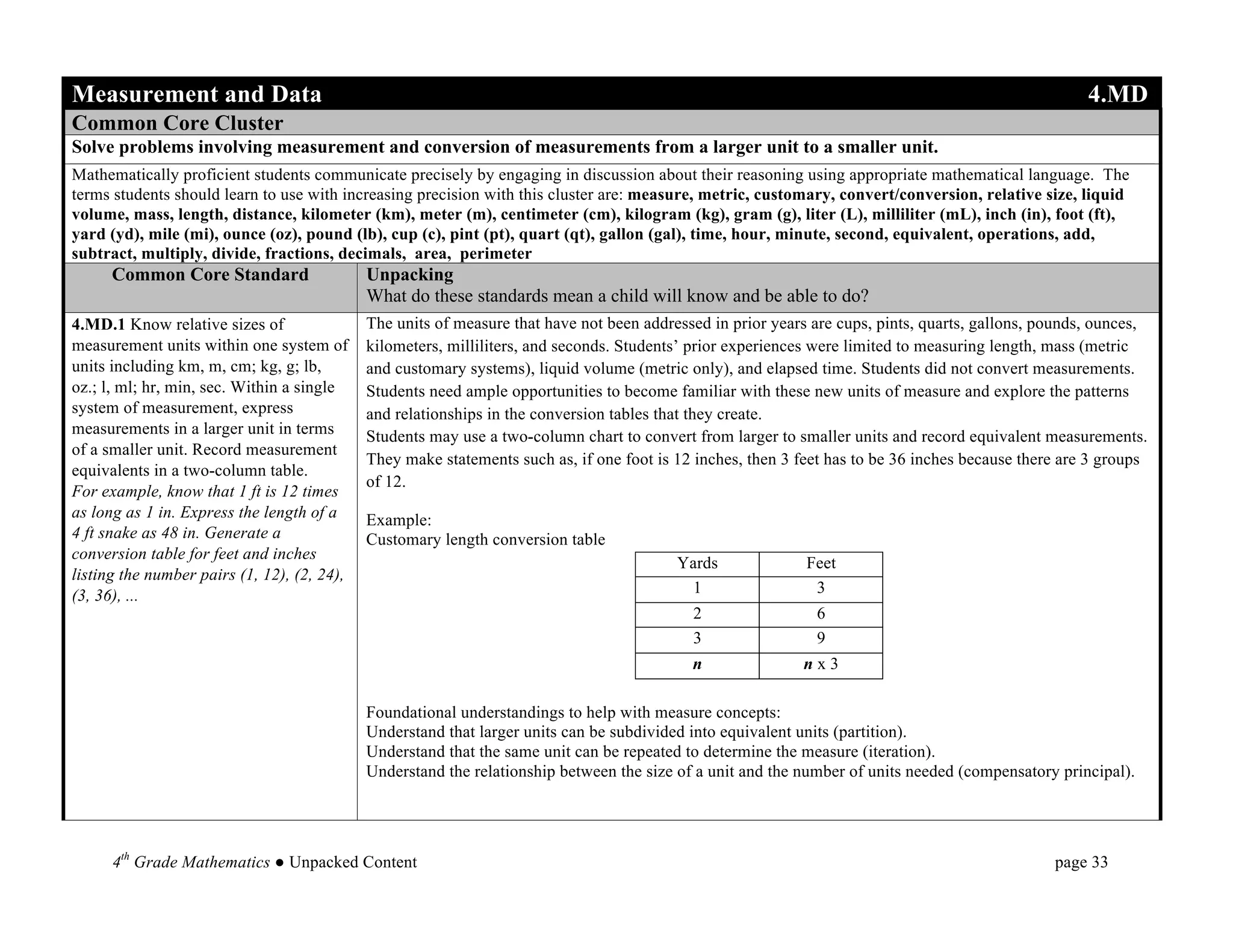
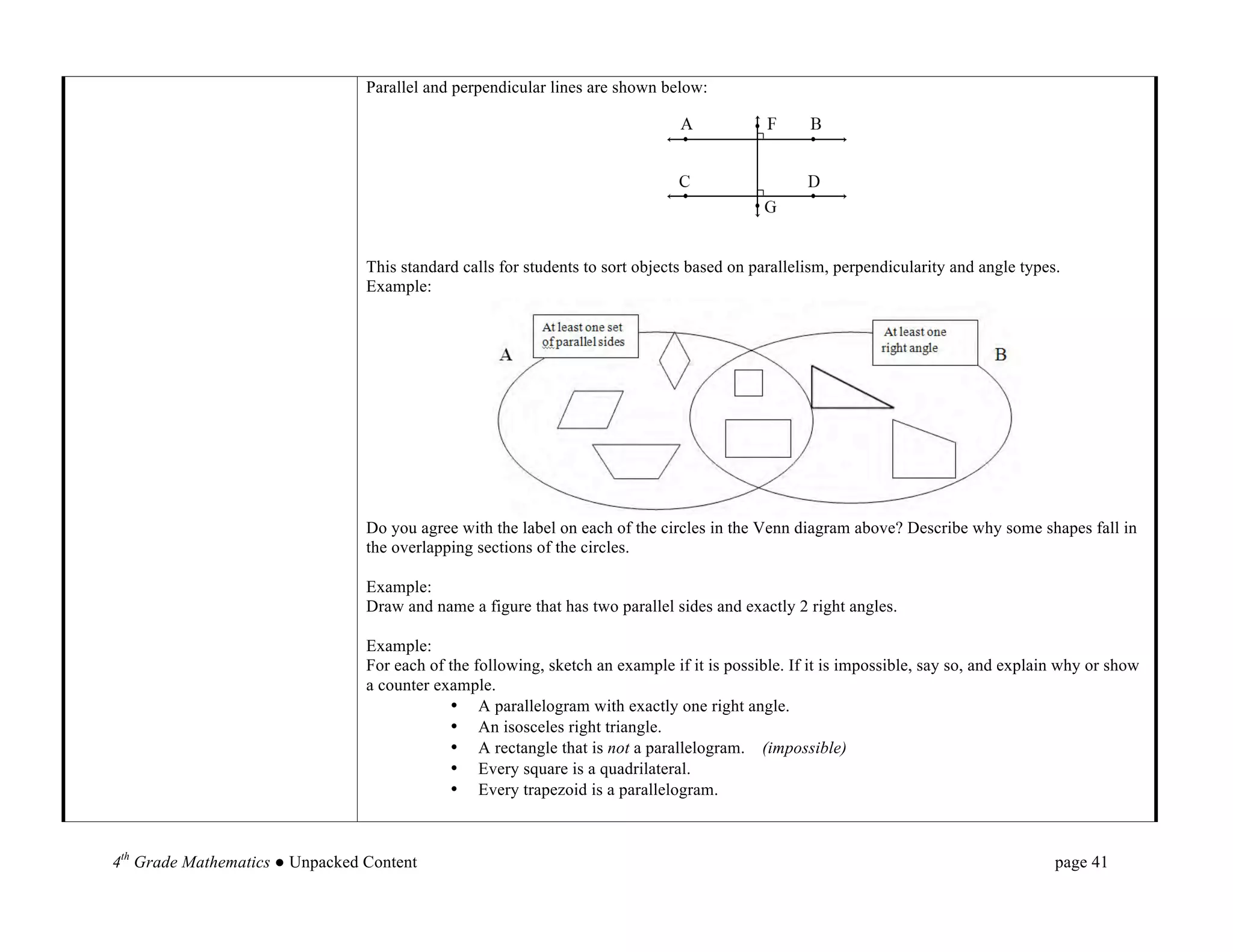
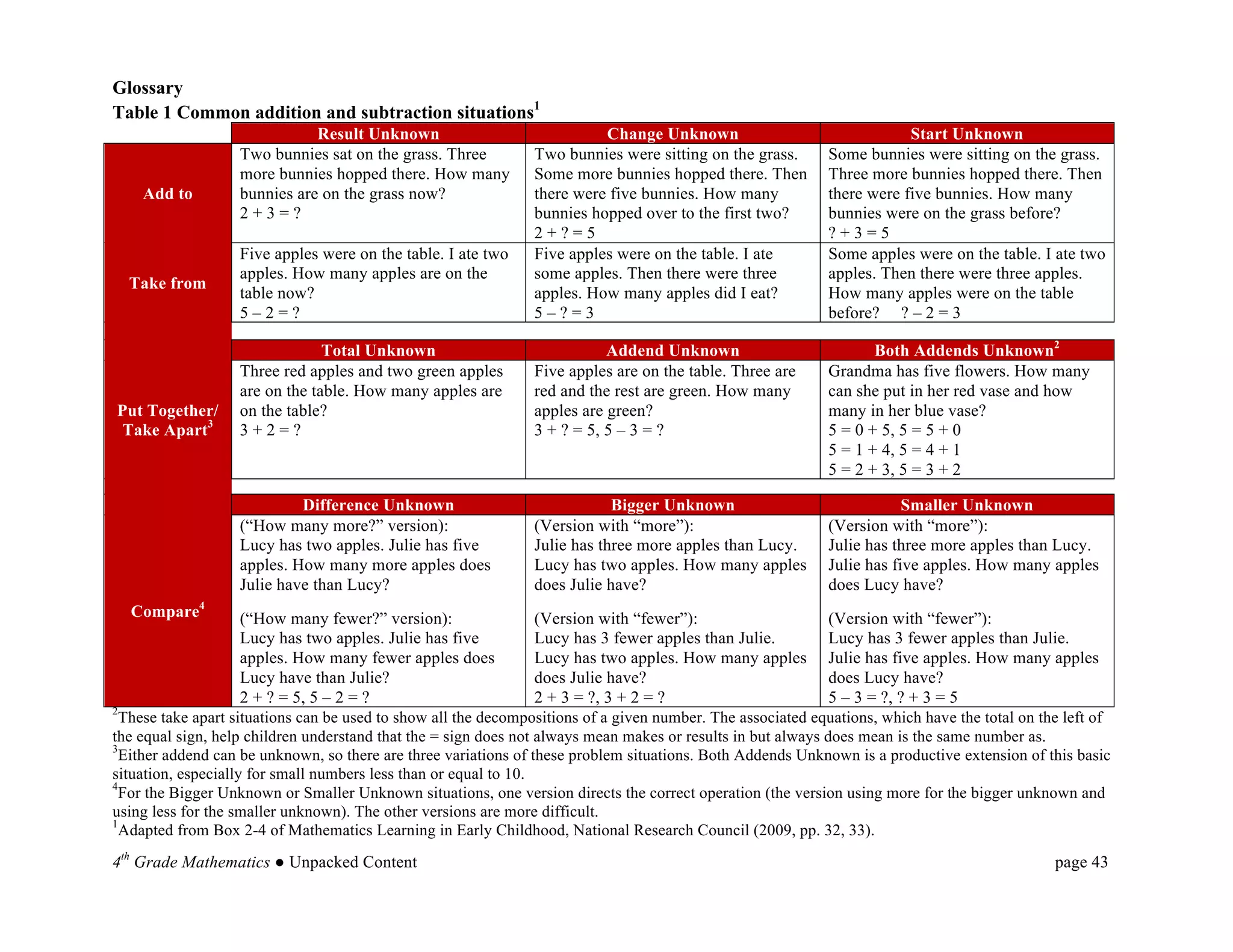
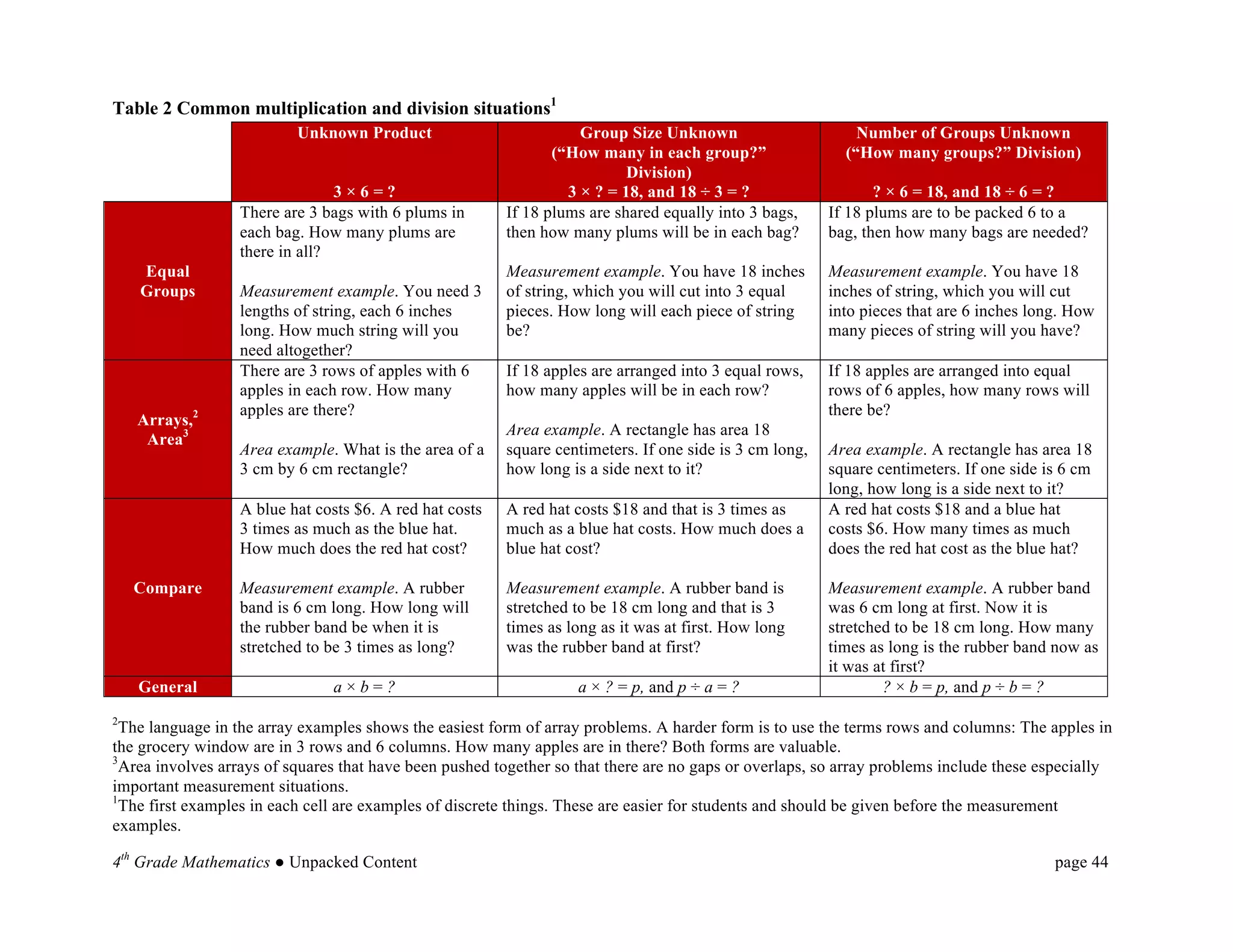
This document provides an overview and unpacking of the 4th grade mathematics Common Core State Standards that will be implemented in North Carolina schools in 2012-2013. It is intended to help educators understand what students need to know and be able to do to meet the standards. New concepts for 4th grade include factors and multiples, multiplying fractions by whole numbers, and angle measurement. The document also discusses the Standards for Mathematical Practice and the two critical areas of focus for 4th grade: multi-digit multiplication and division.