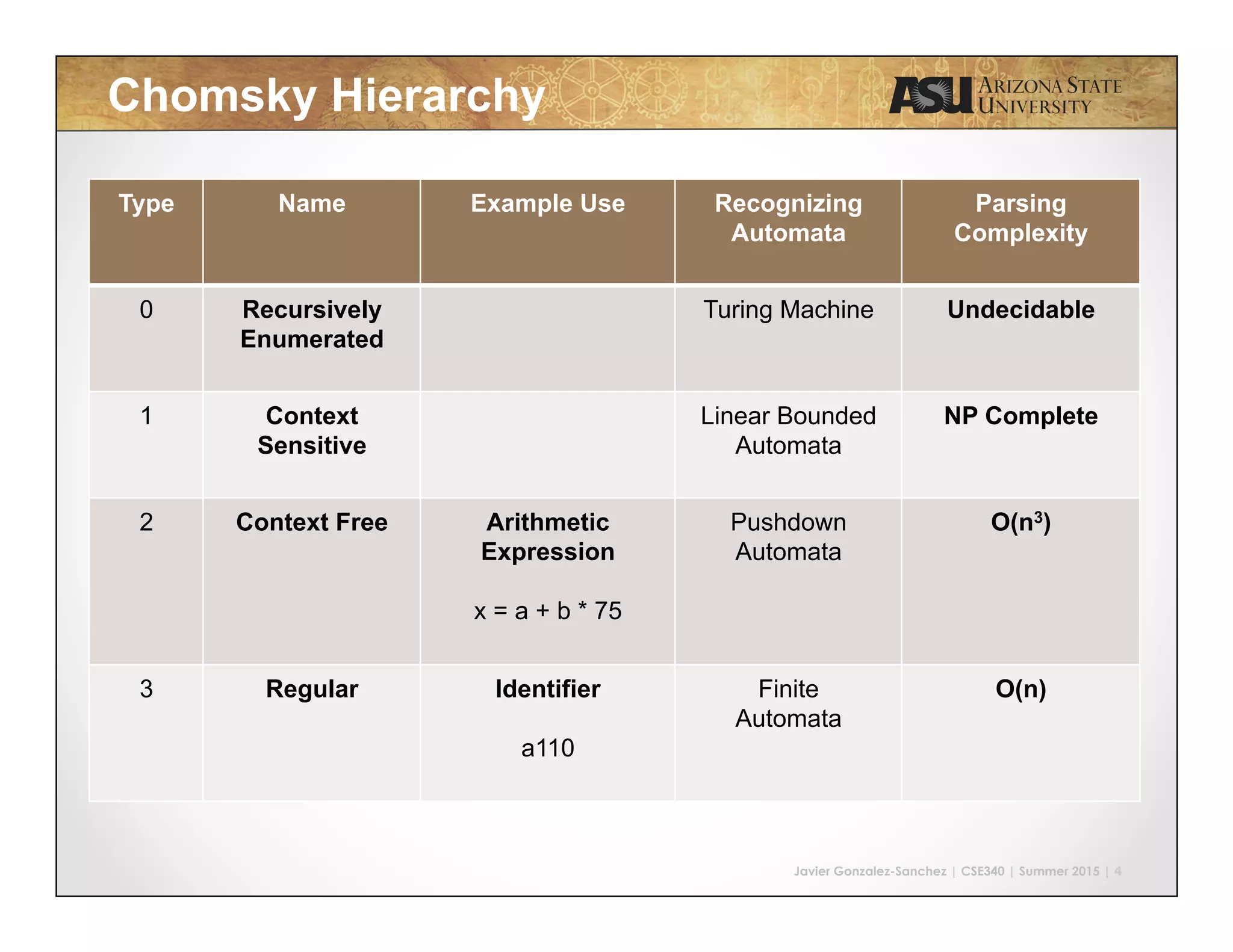
This document contains lecture slides on grammars from a CSE340 class taught by Javier Gonzalez-Sanchez in the summer of 2015. The slides cover the Chomsky hierarchy of formal grammars, including examples of regular, context-free, and context-sensitive grammars. Examples of derivations are provided and grammar types are classified. The slides conclude with a summary of the four grammar types in the Chomsky hierarchy.

1. CSE340 - Principles of
Programming Languages
Lecture 16:
Grammars III
Javier Gonzalez-Sanchez
javiergs@asu.edu
BYENG M1-38
Office Hours: By appointment

2. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 2
Chomsky Hierarchy
*Noam Chomsky

3. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 3
Chomsky Hierarchy

4. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 4
Chomsky Hierarchy
Type Name Example Use Recognizing
Automata
Parsing
Complexity
0 Recursively
Enumerated
Turing Machine Undecidable
1 Context
Sensitive
Linear Bounded
Automata
NP Complete
2 Context Free Arithmetic
Expression
x = a + b * 75
Pushdown
Automata
O(n3)
3 Regular Identifier
a110
Finite
Automata
O(n)

5. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 5
Chomsky Hierarchy
Type 0 - Recursively Enumerated
structure: α → β
where α and β are any string of terminals and nonterminals
Type 1 - Context-sensitive
structure: αXβ → αγβ
where X is a non-terminal, and α,β,γ are any string of terminals and nonterminals, (γ
must be non-empty).
Type 2 - Context-free
structure: X → γ|ε
where X is a nonterminal and γ is any string of terminals and nonterminals (may be
empty). It is discouraged to use only one nonterminal as γ.
Type 3 – Regular
structure: X → αY | α |ε
where X,Y are single nonterminals, and α is a string of terminals;

6. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 6
Regular Grammar
Type 3 – Regular
structure: X → αY | α |ε
where X,Y are single nonterminals, and α is a string of terminals;
<DIGIT> → integer| | integer<DIGIT>
<Q0> → a<Q1> | b<Q0>
<Q1> → a<Q1> | b<Q0> | ε
<S> → a<S> |b<A>
<A> → c<A> | ε
<A> → ε
<A> → a
<A> → <B>a

7. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 7
Regular Grammar
Right Regular Grammars:
Rules of the forms
<A> → ε
<A> → a
<A> → a<B>
A,B: nonterminals and
a: terminal
The Regular Grammars are either left of right:
Left Regular Grammars:
Rules of the forms
<A> → ε
<A> → a
<A> → <B>a
A,B: nonterminals and
a: terminal

8. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 8
Regular Grammar
• Key point: The derivation process is “linear”
• Example of Derivation process:
<S> → a<S> | b<A>
<A> → c<A> | ε
The grammar is equivalent to the regular expression a*bc*
S → aS → aaS → …
→ a…aS →a…abA →a…abcA
→ a…abccA → …
→ a…abc…c

9. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 9
Context-Free Grammar
Type 2 - Context-free
structure: X → γ|ε
where X is a nonterminal and γ is any string of terminals and
nonterminals (may be empty). It is discouraged to use only one
nonterminal as γ.
<S> → <A><S> | ε
<A> → 0 <A> 1| <A>1 | 0 1
<S> → <NP><VP>
<NP> → the <N>
<VP> → <V><NP>
<V> → sings | eats
<N> → cat | song | canary

10. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 10
Context-Sensitive Grammar
Type 1 - Context-sensitive
structure: αXβ → αγβ
where X is a non-terminal, and α,β,γ are any string of terminals
and nonterminals, (γ must be non-empty).
<S>→ a<S><B><C>
<S> → a<B><C>
<C><B> → <H><B>
<H><B> → <H><C>
<H><C> → <B><C>
a<B> → a b
b<B> → b b
b<C> → b c
c<C> → c c
*The language generated by this grammar is {anbncn|n ≥ 1} .

11. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 11
Chomsky Hierarchy
Type 0 - Recursively Enumerated
structure: α → β
where α and β are any string of terminals and nonterminals
Type 1 - Context-sensitive
structure: αXβ → αγβ
where X is a non-terminal, and α,β,γ are any string of terminals and nonterminals, (γ
must be non-empty).
Type 2 - Context-free
structure: X → γ|ε
where X is a nonterminal and γ is any string of terminals and nonterminals (may be
empty). It is discouraged to use only one nonterminal as γ.
Type 3 – Regular
structure: X → αY | α |ε
where X,Y are single nonterminals, and α is a string of terminals;

12. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 12
Exercise
G3 {
<s>à <B><A><B>
<s>à <A><B><A>
<A>à <A><B>
<A>à a<A>
<A>à ab
<B>à <B><A>
<B>à b
}
G4 {
<s>à <A><B>
<A>à a<A>
<A>à a
<B>à <B>b
<B>à b
<A><B>à <B><A>
}
G1 {
<s> à<A>
<s> à<A><A><B>
<A> àaa
<A>a à<A><B>a
<A><B> à<A><B><B>
<B>b à<A><B>b
<B> àb
}
G2 {
<s> à b<s>
<s> à a<A>
<s> à b
<A>à a<s>
<A>à b<A>
<A>à a
}

13. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 13
Examples

14. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 14
Types of Grammars
<E> → e<E>
<E> → <F>
<F> → <F>f
<F> → ε
Is this a regular grammar (X → αY | α |ε) ?
Is this a context-free grammar (X → γ|ε ) ?
Is this a context-sensitive grammar (αXβ → αγβ) ?

15. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 15
Types of Grammars
if <condition> then → if “(“ <condition> “)” then
<condition> → <A> “=“ <B>
Is this a regular grammar (X → αY | α |ε) ?
Is this a context-free grammar (X → γ|ε ) ?
Is this a context-sensitive grammar (αXβ → αγβ) ?

16. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 16
Types of Grammars
if “(“ <condition> “)” then → if <condition> then
<condition> → <A> “=“ <B>
Is this a regular grammar (X → αY | α |ε) ?
Is this a context-free grammar (X → γ|ε ) ?
Is this a context-sensitive grammar (αXβ → αγβ) ?

17. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 17
Types of Grammars
<A> → ε
Is this a regular grammar (X → αY | α |ε) ?
Is this a context-free grammar (X → γ|ε ) ?
Is this a context-sensitive grammar (αXβ → αγβ) ?

18. Javier Gonzalez-Sanchez | CSE340 | Summer 2015 | 18
Chomsky Hierarchy
Type 0 - Recursively Enumerated
structure: α → β
where α and β are any string of terminals and nonterminals
Type 1 - Context-sensitive
structure: αXβ → αγβ
where X is a non-terminal, and α,β,γ are any string of terminals and nonterminals, (γ
must be non-empty).
Type 2 - Context-free
structure: X → γ|ε
where X is a nonterminal and γ is any string of terminals and nonterminals (may be
empty). It is discouraged to use only one nonterminal as γ.
Type 3 – Regular
structure: X → αY | α |ε
where X,Y are single nonterminals, and α is a string of terminals;

19. CSE340 - Principles of Programming Languages
Javier Gonzalez-Sanchez
javiergs@asu.edu
Summer 2015
Disclaimer. These slides can only be used as study material for the class CSE340 at ASU. They cannot be distributed or used for another purpose.