Mutual exclusion

Mutual Exclusion
By Shiran Mizrahi

Critical Section
class Counter {
private int value = 1; //counter starts at one
public Counter(int c) { //constructor initializes counter
value = c;
}
public int inc() { //increment value & return prior value
int temp = value; //start of danger zone
value = temp+1; //end of danger zone
return temp;
}

Critical Section
 The problem occurs if two threads both read
the value field at the line marked “start of
danger zone”, and then both update that field
at the line marked “end of danger zone”.
int temp = value;
value = temp+1;

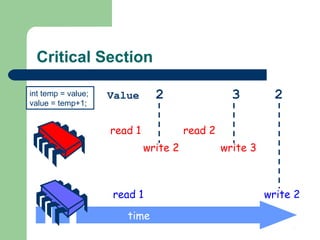
Critical Section
Value
read 1
read 1
write 2
read 2
write 3
write 2
2 3 2
time
int temp = value;
value = temp+1;

The mutual exclusion problem
remainder coderemainder code
entry codeentry code
critical sectioncritical section
exit codeexit code
The problem is to
design the entry
and exit code in a
way that
guarantees that
the mutual
exclusion and
deadlock-freedom
properties are
satisfied.

Good properties
 Mutual Exclusion: No two threads are in their critical sections at the
same time.
 Deadlock-freedom: If a thread is trying to enter its critical section, then
some thread, not necessarily the same one, eventually enters its
critical section.
 Starvation-freedom: If a thread is trying to enter its critical section, then
this thread must eventually enter its critical section.
 Starvation-freedom is a stronger property than Deadlock-freedom.
 Mutual Exclusion: No two threads are in their critical sections at the
same time.
 Deadlock-freedom: If a thread is trying to enter its critical section, then
some thread, not necessarily the same one, eventually enters its
critical section.
 Starvation-freedom: If a thread is trying to enter its critical section, then
this thread must eventually enter its critical section.
 Starvation-freedom is a stronger property than Deadlock-freedom.

Discussion Topics
 The mutual exclusion problem and proposed
algorithms
 Peterson’s algorithm
 Kessels’ single-writer algorithm
 Tournament algorithms
 The Filter algorithm
 The Bakery algorithm
 The mutual exclusion problem and proposed
algorithms
 Peterson’s algorithm
 Kessels’ single-writer algorithm
 Tournament algorithms
 The Filter algorithm
 The Bakery algorithm

Proposed solutions for two threads
We begin with two inadequate
but interesting algorithms

Some notations
 A  B
event A precedes event B
 CSA
thread A is in the critical section
 writeA(x=v)
the event in which thread A writes to x
 readA(x==v)
the event in which thread A reads from x

Algorithm 1
Thread 0
flag[0] = true
while (flag[1]) {}
critical section
flag[0]=false
Thread 1
flag[1] = true
while (flag[0]) {}
critical section
flag[1]=false

Mutual Exclusion
Algorithm 1 satisfies
mutual exclusion

Proof
 Assume in the contrary that two threads can be in their critical
section at the same time.
 From the code we can see:
write0(flag[0]=true)  read0(flag[1]==false)  CS0
write1(flag[1]=true)  read1(flag[0]==false)  CS1
 From the assumption:
read0(flag[1]==false)  write1(flag[1]=true)
Thread 0
flag[0] = true
while (flag[1]) {}
critical section
flag[0]=false
Thread 1
flag[1] = true
while (flag[0]) {}
critical section
flag[1]=false

Proof
 We get:
write0(flag[0]=true)  read0(flag[1]==false) 
write1(flag[1]=true) read1(flag[0]==false)
 That means that thread 0 writes (flag[0]=true) and then thread 1
reads that (flag[0]==false), a contradiction.
Thread 0
flag[0] = true
while (flag[1]) {}
critical section
flag[0]=false
Thread 1
flag[1] = true
while (flag[0]) {}
critical section
flag[1]=false

Deadlock freedom
Thread 0
flag[0] = true
while (flag[1]) {}
critical section
flag[0]=false
Thread 1
flag[1] = true
while (flag[0]) {}
critical section
flag[1]=false
 Algorithm 1 fails dead-lock freedom:
 Concurrent execution can deadlock.
 If both threads write flag[0]=true and flag[1]=true
before reading (flag[0]) and (flag[1]) then both
threads wait forever.

Algorithm 2
Thread 0
victim = 0;
while (victim == 0) {};
critical section
Thread 1
victim = 1;
critical section

Mutual Exclusion
Algorithm 2 satisfies
mutual exclusion

Proof
 Assume in the contrary that two threads can be in
their critical section at the same time.
 From the code we can see:
write0(victim=0)  read0(victim==1) CS0
write1(victim=1)  read1(victim==0)  CS1
Thread 0
victim = 0;
critical section
Thread 1
victim = 1;
critical section

Proof
 Since thread 1 must assign 1 to victim between the events
write0(victim=0) and read0(victim==1), and since this
assignment is the last, we get:
write0(victim=0)  write1(victim=1)  read0(victim==1)
 Once victim is set to 1, it does not change, so every read will
return 1, and this is a contradiction to the former equation:
write1(victim=1)  read1(victim==0)  CS1
Thread 0
victim = 0;
while (victim == 0) }{;
critical section
Thread 1
victim = 1;
critical section

Deadlock freedom
 Algorithm 2 also fails deadlock freedom.
 It deadlocks if one thread runs completely before
the other.
Thread 0
victim = 0;
critical section
Thread 1
victim = 1;
critical section

Algorithms for Two Threads
 We’ll describe two algorithms that solve the
mutual exclusion problem for two Threads.
They are also deadlock-free and starvation
free.

Peterson’s Algorithm
Thread 0
flag[0] = true
victim = 0
while (flag[1] and victim == 0)
}skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
victim = 1
while (flag[0] and victim == 1)
}skip{
critical section
flag[1] = false

Peterson’s Algorithm
 0/1 indicates that the thread is contending for the critical
section by setting flag[0]/flag[1] to true.
 victim shows who got last
 Then if the value of flag[i] is true then there is no contending
by other thread and the thread can start executing the critical
section. Otherwise the first who writes to victim is also the
first to get into the critical section
Thread 0
flag[0] = true
victim = 0
while (flag[1] and
victim == 0) }skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
victim = 1
while (flag[0] and
victim == 1) }skip{
critical section
flag[1] = false

Schematic for Peterson’s mutual exclusion algorithmSchematic for Peterson’s mutual exclusion algorithm
Indicate contending
flag[i] := true
Indicate contending
flag[i] := true
Barrier
victim := i
Barrier
victim := i
Contention?
flag[j] = true ?
Contention?
flag[j] = true ?
critical sectioncritical section
exit code
flag[i] = false
exit code
flag[i] = false
First to cross
the barrier?
victim = j ?
First to cross
the barrier?
victim = j ?yes
yes
no / maybe
no
The structure shows that the
first thread to cross the barrier is
the one which gets to enter the
critical section. When there is no
contention a thread can enter the
critical section immediately.

Mutual Exclusion
Peterson’s algorithm
satisfies mutual exclusion

Proof
 Assume in the contrary that two threads can be in their
critical section at the same time.
 From the code we see:
(*) write0(flag[0]=true)  write0(victim=0) 
read0(flag[1])  read0(victim)  CS0
write1(flag[1]=true)  write1(victim=1)  read1(flag[0])
 read1(victim)  CS1
Thread 0
flag[0] = true
victim = 0
while (flag[1] and
victim == 0) }skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
victim = 1
while (flag[0] and
victim == 1) }skip{
critical section
flag[1] = false

Proof
 Assume that the last thread to write to victim was 0. Then:
write1(victim=1)  write0(victim=0)
 This implies that thread 0 read that victim=0 in equation (*)
 Since thread 0 is in the critical section, it must have read
flag[1] as false, so:
write0(victim=0)  read0(flag[1]==false)
Thread 0
flag[0] = true
victim = 0
while (flag[1] and
victim == 0) }skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
victim = 1
while (flag[0] and
victim == 1) }skip{
critical section
flag[1] = false

Proof
 Then, we get:
write1(flag[1]=true)  write1(victim=1) 
write0(victim=0)  read0(flag[1]==false)
 Thus:
write1(flag[1]=true)  read0(flag[1]==false)
 There was no other write to flag[1] before the critical
section execution and this yields a contradiction.
Thread 0
flag[0] = true
victim = 0
while (flag[1] and
victim == 0) }skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
victim = 1
while (flag[0] and
victim == 1) }skip{
critical section
flag[1] = false

Starvation freedom
Peterson’s algorithm
is starvation-free

Proof
 Assume to the contrary that the algorithm is not
starvation-free
 Then one of the threads, say thread 0, is forced to
remain in its entry code forever
Thread 0
flag[0] = true
victim = 0
while (flag[1] and
victim == 0) }skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
victim = 1
while (flag[0] and
victim == 1) }skip{
critical section
flag[1] = false

Proof
 This implies that at some later point thread 1 will do
one of the following three things:
1. Stay in its remainder forever
2. Stay in its entry code forever, not succeeding and
proceeding into its critical section
3. Repeatedly enter and exit its critical section
Thread 0
flag[0] = true
victim = 0
while (flag[1] and
victim == 0) }skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
victim = 1
while (flag[0] and
victim == 1) }skip{
critical section
flag[1] = false
We’ll show that each of
the three possible cases
leads to a contradiction.

Proof
 In the first case flag[1] is false, and hence thread 0 can
proceed.
 The second case is impossible since victim is either 0 or 1, and
hence it always enables at least one of the threads to proceed.
 In the third case, when thread 1 exit its critical section and tries
to enter its critical section again, it will set victim to 1 and will
never change it back to 0, enabling thread 0 to proceed.
Thread 0
flag[0] = true
victim = 0
while (flag[1] and
victim == 0) }skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
victim = 1
while (flag[0] and
victim == 1) }skip{
critical section
flag[1] = false

Kessels’ single-writer Algorithm
What if we replace the multi-writer register victim with two single-
writer registers. What is new algorithm?
Answer (Kessels’ Alg.)
victim = 0  victim[0] =victim[1]
victim = 1  victim[0] ≠victim[1]

Kessels’ single-writer Algorithm
Thread 0
flag[0] = true
local[0] = victim[1]
victim[0] = local[0]
while (flag[1] and
local[0]=victim[1]) }skip{
critical section
flag[0] = false
Thread 1
flag[1] = true
local[1]=1-victim[0]
victim[1] = local[1]
while (flag[0] and
local[1] ≠ victim[0])) }skip{
critical section
flag[1] = false
Thread 0 can write the registers victim[0] and flag[0]
and read the registers victim[1] and flag[1]
Thread 1 can write the registers victim[1] and flag[1]
and read the registers victim[0] and flag[0]

Solutions for Many Threads
How can we use a two-thread algorithm to
construct an algorithm for many threads?
How can we use a two-thread algorithm to
construct an algorithm for many threads?

Tournament Algorithms
1 2 3 4 5 6 7 8

Tournament Algorithms
 A simple method which enables the construction an
algorithm for n threads from any given algorithm for
two threads.
 Each thread is progressing from the leaf to the root,
where at each level of the tree it participates in a two
thread mutual exclusion algorithm.
 As a thread advanced towards the root, it plays the
role of thread 0 when it arrives from the left subtree,
or of thread 1 when it arrives from the right subtree.

The Filter Algorithm for n Threads
 A direct generalization of Peterson’s algorithm
to multiple threads.
 The Peterson algorithm used a two-element
boolean flag array to indicate whether a
thread is interested in entering the critical
section. The filter algorithm generalizes this
idea with an N-element integer level array,
where the value of level[i] indicates the latest
level that thread i is interested in entering.
ncs
cslevel n-1

Filter
 There are n-1 “waiting rooms” called levels
 At each level
– At least one enters level
– At least one blocked if
many try
 Only one thread makes it through
ncs
cs
level 0
level n-1

The Filter Algorithm
Thread i
for (int L = 1; L < n; L++) {
level[i] = L;
victim[L] = i;
while ((∃ k != i level[k] >= L) and victim[L] == i ) {}
}
critical section
level[i] = 0;

Thread i
for (int L = 1; L < n; L++) {
level[i] = L;
victim[L] = i;
}
critical section
level[i] = 0;
Filter
One level at a time

Filter
Thread i
for (int L = 1; L < n; L++) {
level[i] = L;
victim[L] = i;
}
critical section
level[i] = 0;
Announce intention to enter level L

Filter
Thread i
for (int L = 1; L < n; L++) {
level[i] = L;
victim[L] = i;
}
critical section
level[i] = 0;
Give priority to anyone but me (at every level)

Filter
Thread i
for (int L = 1; L < n; L++) {
level[i] = L;
victim[L] = i;
}
critical section
level[i] = 0;
Wait as long as someone else is at same or higher level,
and I’m designated victim.
Thread enters level L when it completes the loop.

Claim
 There are at most n-L threads enter level L
 Proof: by induction on L and by contradiction
 At L=0 – trivial
 Assume that there are at most n-L+1 threads at level
L-1.
 Assume that there are n-L+1 threads at level L
 Let A be the last thread to write victim[L] and B any
other thread at level L

Proof structure
ncs
cs
Assumed to enter L-1
By way of contradiction
all enter L
n-L+1 = 4
n-L+1 = 4
A B
Last to
write
victim[L]
Show that A must have seen
B at level L and since victim[L] == A
could not have entered

Proof
 From the code we get:
 From the assumption:
writeB(level[B]=L)writeB(victim[L]=B)
writeA(victim[L]=A)readA(level[B])
writeB(victim[L]=B)writeA(victim[L]=A)
for (int L = 1; L < n; L++) {
level[i] = L;
victim[L] = i;
}
critical section
level[i] = 0;

Proof
 When combining all we get:
 Since B is at level L, when A reads level[B], it
reads a value greater than or equal L and so A
couldn’t completed its loop and still waiting
(remember that victim=A), a contradiction.
writeB(level[B]=L) readA(level[B])
for (int L = 1; L < n; L++) {
level[i] = L;
victim[L] = i;
}
critical section
level[i] = 0;

A conclusion
 The filter algorithm satisfies
mutual exclusion
 At level n-1 there are at most n-(n-1)=1
threads, which means at most one thread in
the critical section

Starvation-freedom
 Filter Lock satisfies properties:
– Just like Peterson algorithm at any level
– So no one starves

Fairness
 Starvation freedom guarantees that if a
thread is trying to enter its critical section, it
will eventually do so
 There is no guarantee about how long it will
take
 We wish for fairness: if thread A enters the
entry code before thread B, then A should
enter the critical section first

Bounded waiting
 We divide our method into two parts:
Doorway interval:
- Written DA
- always finishes in finite steps
Waiting interval:
- Written WA
- may take unbounded steps
entry code
exit code
critical
section
remainder
doorway
waiting

The mutual exclusion problem
 Mutual Exclusion
 Deadlock-freedom
 Starvation-freedom
 FIFO

r-Bounded Waiting
 For threads A and B:
– If DA
k
 DB
j
 A’s k-th doorway precedes B’s j-th doorway
– Then CSA
k
 CSB
j+r
 A’s k-th critical section precedes B’s (j+r)-th critical
section
 B cannot overtake A by more than r times
 First-come-first-served means r = 0.

Fairness in Filter Algorithm
 Filter satisfies properties:
– No one starves
– But very weak fairness
Not r-bounded for any r!
– That’s pretty lame…

Bakery Algorithm
 The idea is similar to a line at the bakery
 A customer takes a number greater than
numbers of other customers
 Each of the threads gets a unique identifier

Bakery Algorithm
Thread i
flag[i]=true;
number[i] = max(number[0], …,number[n-1])+1;
while (∃ k!= i
flag[k] && (number[i],i) > (number[k],k)) {};
critical section
flag[i] = false;

Bakery Algorithm
flag[i]=true;
while (∃ k!= i
critical section
flag[i] = false;
Doorway

Bakery Algorithm
flag[i]=true;
while (∃ k!= i
critical section
flag[i] = false;
I’m interested

Bakery Algorithm
flag[i]=true;
while (∃ k!= i
critical section
flag[i] = false;
Take an number
numbers are always increasing!

Bakery Algorithm
flag[i]=true;
while (∃ k!= i
critical section
flag[i] = false;
Someone is interested

Bakery Algorithm
flag[i]=true;
while (∃ k!= i
critical section
flag[i] = false;
There is someone with a lower
number and identifier.
pair (a,b) > (c,d) if a>c, or a=c and b>d
(lexicographic order)

Deadlock freedom
 The bakery algorithm is deadlock free
 Some waiting thread A has a unique least
(number[A],A) pair, and that thread can enter
the critical section

FIFO
 The bakery algorithm is first-come-first-
served
 If DA  DB then A’s number is earlier
– writeA(number[A])  readB(number[A]) 
writeB(number[B])  readB(flag[A])
 So B is locked out while flag[A] is true
flag[i]=true;
while (∃ k!= i
critical section
flag[i] = false;

Starvation freedom
 The bakery algorithm satisfies deadlock
freedom and first-come-first-served and
those properties implies starvation freedom

Mutual Exclusion
 Suppose A and B in CS together
 Suppose A has an earlier number
 When B entered, it must have seen
– flag[A] is false, or
– number[A] > number[B]
flag[i]=true;
while (∃ k!= i
critical section
flag[i] = false;

Mutual Exclusion
 numbers are strictly increasing so
 B must have seen (flag[A] == false)
 numberingB  readB(flag[A])  writeA(flag[A]) 
numberingA
 Which contradicts the assumption that A has
an earlier number
flag[i]=true;
while (∃ k!= i
critical section
flag[i] = false;

Mutual exclusion

More Related Content

What's hot

Viewers also liked

Similar to Mutual exclusion

Recently uploaded

Mutual exclusion