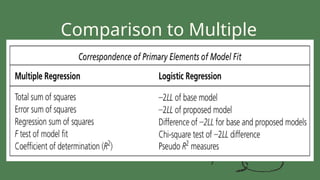
The document outlines advanced statistical methods, focusing on multiple discriminant analysis and logistic regression. It describes their applications for predicting categorical and binary dependent variables, emphasizing design rules and understanding covariance matrices. Key comparisons between the two methods are presented, highlighting the strengths and weaknesses in handling variable types and assumptions.