Mountain Range Options

Copyright © Arkus Financial Services - 2014
Mountain Range options
Page 1
MOUNTAIN RANGE OPTIONS Paolo Pirruccio

Page 2
►Originally marketed by Société Générale in 1998.
►Traded over-the-counter (OTC), typically by private banks and institutional investors such as hedge funds.
►These options have combined characteristics of Range (multi – year time ranges) and Basket options (more than one underlying).
Introduction

Page 3
Being struck on two or more underlying assets, mountain range options are particularly relevant for hedgers who want to cover several positions with one derivative. Instead of monitoring multiple options written on individual assets, a basket option can be structured to achieve the same coverage. The advantage of this feature is that the combined volatility will be lower than the volatility of the individual assets. A lower volatility will result in a cheaper option price, which can significantly decrease the costs implied by hedging. All these features made Mountain Range Options an appealing product which usually offer a minimum capital guarantee, plus the variable part of returns determined by the stock performances. It can be useful for investors who want a capital protection.
Usage

Page 4
Himalayan - based on the performance of the best asset in the portfolio.
Altiplano - in which a vanilla option is combined with a compensatory coupon payment if the underlying security never reaches its strike price during a given period.
Annapurna - in which the option holder is rewarded if all securities in the basket never fall below a certain price during the relevant time period.
Atlas - in which the best and worst- performing securities are removed from the basket prior to execution of the option.
Everest - a long-term option in which the option holder gets a payoff based on the worst-performing securities in the basket.
3.300 m -
4.167 m -
8.000 m -
8.091 m -
8.848 m -
Definition and types

Risk-based Governance Solutions
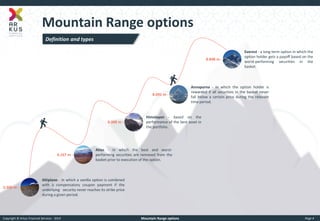
Altiplano Options
Al·ti·pla·no [al-tuh-plah-noh; for 1 also Spanish ahl-tee-plah-naw]
1.A plateau region in South America, situated in the Andes of Argentina, Bolivia and Peru.
2.Financial instrument in which a vanilla option is combined with a compensatory coupon payment if the underlying security never reaches its strike price during a given period.

Page 6
“Altiplano con Memoria” Options
푷풂풚풐풇풇풊=휼 푵 ∗푪 ∗풊 풊풇 풊=ퟏ 푷풂풚풐풇풇(풊)=휼 (푵 ∗푪 ∗풊 − 푪풏) 풊−ퟏ 풏=ퟏ 풊풇 풊=ퟐ,ퟑ,..,풏
휼= ퟏ 풊풇 푴풊풏 ퟏ≤풋≤풏,풕ퟏ≤풕≤풕ퟐ 푺풋 풕 푺풋 ퟎ≥푳 ퟎ 풆풍풔풆
►The Payoff is thus different from zero only if none of the stocks is below the barrier during the specified time period
►C is a fixed coupon payment
►i is the Barrier Observation Date
►Sj represents the value of the j-th stock
►휼 is a binary variable equal to the condition set for the barrier value
►L is the predetermined limit
Payoff structure

Page 7
1.Generate normally distributed random variates through the Inverse Transform Method
2.Simulate the correlated multi asset path through the Cholesky Decomposition
3.Check, for each barrier observation date, if each single underlying is above the barrier limit
If one of the underlying assets is below the barrier limit  Payoff(i) = 0
If none of the underlying assets is below the barrier limit: 푷풂풚풐풇풇풊=휼 푵 ∗푪 ∗풊 풊풇 풊=ퟏ 푷풂풚풐풇풇(풊)=휼 (푵 ∗푪 ∗풊 − 푪풏) 풊−ퟏ 풏=ퟏ 풊풇 풊=ퟐ,ퟑ,..,풏
4.Store the payoff values into an array and discount each of them back at the appropriate discount rate
5.Sum all the discounted payoffs to get the present value of the option
6.Repeat the first 5 steps 20.000 times, to build a distribution of possible option values
7.Take the average of all simulation outcomes to find the final price
8.Greeks Estimation - Delta
Pricing – The algorithm

Page 8
Consider an integral on the unit interval [0,1]:
푰= 품풙풅풙 ퟏ ퟎ
We may think of this integral as the expected value E[g(U)], where U is a uniform random variable on the interval (0,1) and estimate the expected value - a number – by a sample mean (which is a random variable).
The only thing we have to do is generating a sequence Ui of independent random samples from the uniform distribution and then evaluate the sample mean: 푰풎= ퟏ 풎 품(푼풊) 풎 풊=ퟏ
The strong law of large numbers implies that, with probability 1, 풍풊풎 풎 → + ∞ 푰풎=푰
Pricing: the idea behind Monte Carlo Integration

Page 9
Suppose we are given the CDF F(x) = P(X ≤ x), and that we want to generate random variates according to F. If we are able to generate random variates according to F, then we could:
1.Draw a random number U ~ U(0,1)
2.Return X = F-1 (U)
It can be shown that the random variate X generated by this method is characterized by the distribution function F.
For example u = 0.975 would return 1.959, because 97.5% of the probability of a normal pdf occurs in the region where X < 1.959
Pricing – Generating normal random variates through the Inverse Transform Method

Page 10
Consider a multivariate normal distribution with expected value μ and covariance matrix Σ (symmetric positive definite).
The Cholesky Matrix M is a lower triangular matrix such that:
횺= 푴푻퐌 Once retrieved this matrix, we may apply the following algorithm to generate correlated random numbers X:
Generate n independent standard normal variates Z1, Z2 ,..., Zn
Return 푿= 흁+ 푴푻퐙 ,where 풁=Z1, Z2 ,..., ZnT is a vector of uncorrelated variables
Suppose we must generate sample paths for two correlated Wiener processes, having covariance matrix 횺= ퟏ흆 흆ퟏ
It can be verified that the Cholesky Matrix is 퐌= ퟏퟎ 흆(ퟏ−흆ퟐ) .
Hence, to simulate bidimensional correlated Wiener Process, we will create two independent standard normal variates Z1 and Z2 and use:
풙ퟏ= 풁ퟏ and 풙ퟐ= 흆풁ퟏ+ (ퟏ−흆ퟐ)풁ퟐ
Pricing – Correlated Random Numbers: Cholesky Factorization

Page 11
The pricing structure is primarily dependent on the correlation between the constituent stocks.
In this example of a 7 asset basket, a small estimation error of 0.5% for 1 set of correlation, would lead to an estimation error of 10.5%, which in turn would make any final option value meaningless.
This is why, together with analytical difficulties in deriving it for higher - dimensions problems, any closed form would be obsolete when dealing with these options.
Stock
A
B
C
D
E
F
G
A
1
Corr(B,A)
Corr(C,A)
Corr(D,A)
Corr(E,A)
Corr(F,A)
Corr(G,A)
B
Corr(B,A)
1
Corr(C,B)
Corr(D,B)
Corr(E,B)
Corr(F,B)
Corr(G,B)
C
Corr(C,A)
Corr(C,B)
1
Corr(D,C)
Corr(E,C)
Corr(F,C)
Corr(G,C)
D
Corr(D,A)
Corr(D,B)
Corr(D,C)
1
Corr(E,D)
Corr(F,D)
Corr(G,D)
E
Corr(E,A)
Corr(E,B)
Corr(E,C)
Corr(E,D)
1
Corr(F,E)
Corr(G,E)
F
Corr(F,A)
Corr(F,B)
Corr(F,C)
Corr(F,D)
Corr(F,E)
1
Corr(G,F)
G
Corr(G,A)
Corr(G,B)
Corr(G,C)
Corr(G,D)
Corr(G,E)
Corr(G,F)
1
Pricing – the correlation estimation problem and the impossibility to use a closed form

Page 12
For path-dependent options (like Mountain Range Options), we need the whole path or, at least, a sequence of values of the underlying at given time events.
The first step in simulating a price path is to choose a stochastic process to model changes in financial asset prices.
Stock prices are often modelled by the GBM:
풅푺풕=흁푺풕퐝퐭+ 흈푺풕풅푾풕
Using Ito’s Lemma, we may transform the above equation into the following form:
풅풍풐품푺풕=(흁− ퟏ ퟐ 흈ퟐ)풅풕+흈풅푾풕
The last equation is particularly useful, as it can be integrated exactly and discretized, yielding to:
푺풕=푺ퟎ풆(흂휹풕+흈휹풕휺)
Pricing – Path Generation & the Geometric Brownian Motion

Page 13
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
500
525
550
575
600
625
650
675
700
725
750
775
800
825
850
T1
T2
T3
T4
T5
T6
Level of the Underlying
Barrier Observation Dates
Case A: All coupons paid
S1
S2
S3
S4
B1
B2
B3
B4

Page 14
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
500
525
550
575
600
625
650
675
T1
T2
T3
T4
T5
T6
Level of the Underlying
Barrier Observation Dates
Case B – Some coupons paid (C1,C2 & C3) and some not (C4,C5 & C6)
S1
S2
S4
B1
B2
B3
B4
S3

Page 15
Greeks – Estimation - Delta
The Greeks are the quantities representing the sensitivity of the price of derivatives to a change in underlying parameters on which the value of an instrument is dependent.
The Delta, in particular, measures the rate of change of option value with respect to changes in the underlying asset price.
In a Monte Carlo framework, Greeks estimation requires a Finite Difference Approximation approach.
This method is based on the re-calculation of the option value with a slight change of one of the input parameters, so that the sensitivity of the option value to that parameter can be estimated. The parameter in question is the value of the underlying.
휟= 흏풇(푺ퟎ) 흏푺ퟎ =퐥퐢퐦 휹푺ퟎ→ퟎ 풇푺ퟎ+휹푺ퟎ−풇푺ퟎ 휹푺ퟎ
This idea is however to naive and it can be shown that taking a central difference may be preferable in order to reduce the variance of the estimator:
휟= 풇푺ퟎ+휹푺ퟎ,흎−풇푺ퟎ−휹푺ퟎ,흎 ퟐ휹푺ퟎ

Page 16
Should you have any questions…
Paolo Pirruccio
Risk Analyst
paolo.pirruccio@arkus-fs.com

Page 17

Mountain Range Options

More Related Content

What's hot

Viewers also liked

Similar to Mountain Range Options

More from Arkus Financial Services

Recently uploaded

Mountain Range Options