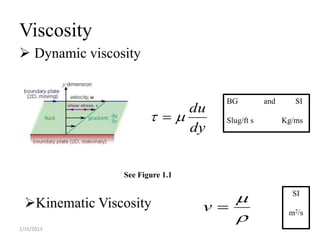
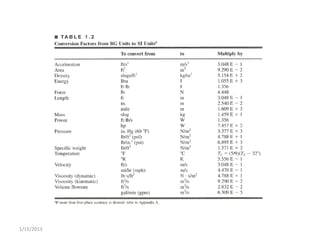
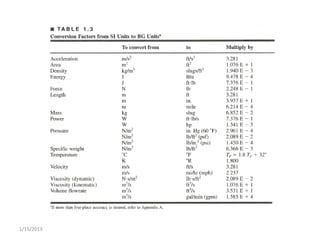
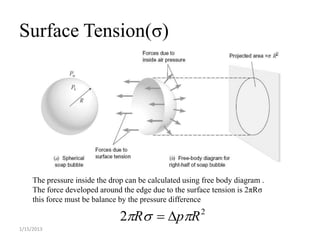
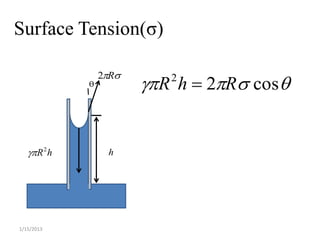
This lecture discusses key concepts in fluid mechanics including density, specific weight, specific gravity, the ideal gas law, viscosity, and surface tension. It defines important terms like density, specific weight, dynamic and kinematic viscosity. Examples are provided to demonstrate calculations for determining density from specific gravity, solving the ideal gas law, and finding surface tension based on tube diameter. Viscosity is explained using equations for both dynamic and kinematic viscosity.

1. MET 212
Fluid Mechanics
Lecture # 2
1/15/2013

2. Objective
 Measures of Fluid Mass and Weight
Density
Specific Wight
Specific Gravity
 Ideal Gas Law
 Viscosity
Dynamic Viscosity
Kinematic Viscosity
 Surface Tension
1/15/2013

3. Measures of Fluid Mass and Weight
 Density
 The density of the fluid designated by Greek symbol (ρ)
 Defined as a mass per unit volume
 Used to characterize the mass of fluid
 BG= slugs/ ft3 and SI= kg/m3
 Specific Weight
 The specific weight of the fluid designated by Greek symbol (γ)
 Defined as weight per unit volume
 Used to characterize the weight of the system
 BG= lb/ ft3 and SI= N/m3
 Specific Gravity
 The specific gravity of the fluid designated by SG
 Defined as a ratio of the density of the fluid to the density of the water
 The density of the water @ 4oC is BG=1.94 slugs/ft3 and SI=1000 kg/m3
1/15/2013

4. Measures of Fluid Mass and Weight
Specific Gravity (Example)
Calculate the density of the mercury in two system
BG and SI by knowing the SGmercury @ 20oC is 13.55
1/15/2013

5. Ideal Gas Law
 Gas are highly compressible in comparison to
liquid, So from the Ideal gas law change in the
temperature or the pressure of the gases can
directly change the density.
p   RT
Where p is the absolute pressure, ρ is the density, T
is the absolute temperature and R is gas constant
 R=R/m
 R is universal gas constant 8314.3J/kg mole K
 m is the molar mass
1/15/2013

6. Ideal Gas Law
Example
The absolute pressure and temperature of a gas in large
chamber are found to be 500 kPa and 60oC respectively. Find
the density if the air has m =28.97
1/15/2013s

7. Viscosity
 Dynamic viscosity
BG and SI
du
  Slug/ft s Kg/ms
dy
See Figure 1.1
Kinematic Viscosity  SI
v
 m2/s
1/15/2013

8. Viscosity
 Example
Determine the value of the Reynolds number using SI system
for fluid with viscosity of 0.38 N.s/m2 and specific gravity of
0.91 flow into pipe with diameter of 25 mm with velocity of
2.6 m/s.
1/15/2013

9. 1/15/2013

10. 1/15/2013

11. Surface Tension
 At interface between a liquid and the gas forces
develop in the liquid surface which case the surface to
behave as “skin” or “membrane”
1/15/2013

12. Surface Tension(σ)
The pressure inside the drop can be calculated using free body diagram .
The force developed around the edge due to the surface tension is 2πRσ
this force must be balance by the pressure difference
2R  pR 2
1/15/2013

13. Surface Tension(σ)
2R
ϴ R h  2R cos
2
R 2 h h
1/15/2013

14. Surface Tension(σ)
Example
What diameter of clean glass tubing is required to
rise water at 20oC in tube to 1mm. Where σ of
water is 0.0728 N/m and the θ =0.
1/15/2013