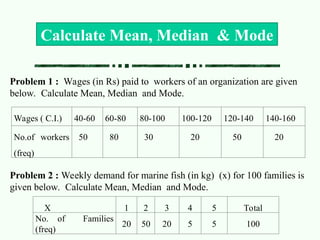
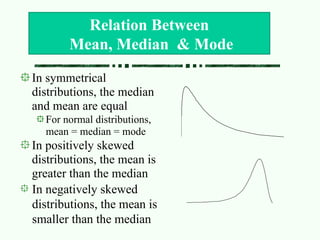
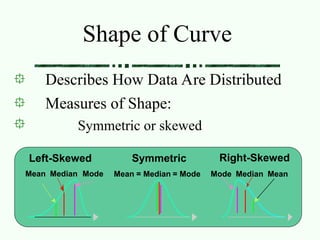
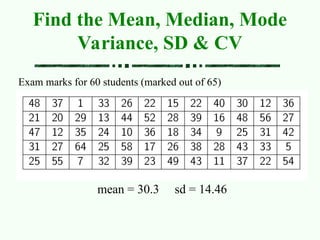
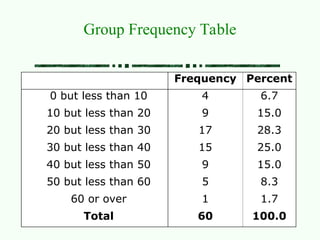
The document covers measures of central tendency including mean, median, and mode, explaining their calculation methods and when to use each measure. It also discusses measures of variation such as variance, standard deviation, and coefficient of variation, highlighting their importance in describing data distributions. Additionally, the relationships between mean, median, and mode in different distributions are illustrated with examples.

2. Summary of Measures
Central Tendency
Mean
Median
Mode
Quartile
Summary Measures
Variation
Variance
Standard Deviation
Coefficient of
Variation
Range

3. Measures of Central Tendency
A measure of central tendency is a
descriptive statistic that describes the
average, or typical value of a set of scores.
There are three common measures of central
tendency:
the mean
the median
the mode

4. The mean is:
the arithmetic average of all the scores
(X)/N
the number, m, that makes (X - m) equal to 0
the number, m, that makes (X - m)2
a
minimum
The mean of a population is represented by
the Greek letter ; the mean of a sample is
represented by X
The Mean

5. Calculating the Mean for
Grouped Data
N
X
f
X


where: f X = a score multiplied by its frequency
0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 12 14
Mean = 5 Mean = 6
Mean affected by extreme values

6. You should use the mean when
the data are interval or ratio scaled
Many people will use the mean with ordinally
scaled data too
and the data are not skewed
The mean is preferred because it is sensitive
to every score
If you change one score in the data set, the
mean will change
When To Use the Mean

7. Calculating the Mean
Calculate the mean of the following data:
1 5 4 3 2
Sum the scores (X):
1 + 5 + 4 + 3 + 2 = 15
Divide the sum (X = 15) by the number of
scores (N = 5):
15 / 5 = 3
Mean = X = 3

8. Find the mean of the following data:
Mean =
[3(10)+10(9)+9(8)+8(7)+10(6)+
2(5)]/42 = 7.57
Score Number of
students
10 3
9 10
8 9
7 8
6 10
5 2
Calculating the Mean for
Grouped Data

9. The Median
The median is simply another name for the
50th
percentile
It is the score in the middle; half of the scores
are larger than the median and half of the scores
are smaller than the median
Not affected by extreme values
0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 12 14
Median = 5 Median = 5

10. How To Calculate the Median
Conceptually, it is easy to calculate the median
There are many minor problems that can occur; it
is best to let a computer do it
Sort the data from highest to lowest
Find the score in the middle
middle = (n + 1) / 2
If n, the number of scores, is even the median is
the average of the middle two scores

11. Calculating the Median for
Grouped Data
h
f
cf
N
l
Median 



2
/
• To use this formula first determine median class.
Median class is that class whose less than type cumulative
frequency is just more than N / 2 ;
• l = lower limit of median class ;
• cf = less than type cumulative frequency of premedian
class;
• f = frequency of median class
• h = class width.

12. When To Use the Median
The median is often used when the
distribution of scores is either positively or
negatively skewed
The few really large scores (positively skewed)
or really small scores (negatively skewed) will
not overly influence the median

13. Median Example
What is the median of the following scores:
10 8 14 15 7 3 3 8 12 10 9
Sort the scores:
15 14 12 10 10 9 8 8 7 3 3
Determine the middle score:
middle = (n + 1) / 2 = (11 + 1) / 2 = 6
Middle score = median = 9

14. Median Example
What is the median of the following scores:
24 18 19 42 16 12
Sort the scores:
42 24 19 18 16 12
Determine the middle score:
middle = (n + 1) / 2 = (6 + 1) / 2 = 3.5
Median = average of 3rd
and 4th
scores:
(19 + 18) / 2 = 18.5

15. The Mode
The mode is the score that occurs most frequently in
a set of data
Not Affected by Extreme Values
There May Not be a Mode
There May be Several Modes
Used for Either Numerical or Categorical Data
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Mode = 9
0 1 2 3 4 5 6
No Mode

16. Calculating the Mode for
Grouped Data
h
f
f
f
f
f
l
Mode
m
m











2
1
1
2
To use this formula first determine modal class.
Modal class is that class which has maximum
frequency ;
l = lower limit of modal class;
fm
= maximum frequency;
f1
= frequency of pre modal class ;
f2
= frequency of post modal class

17. When To Use the Mode
The mode is not a very useful measure of
central tendency
It is insensitive to large changes in the data set
That is, two data sets that are very different from
each other can have the same mode
The mode is primarily used with nominally
scaled data
It is the only measure of central tendency that is
appropriate for nominally scaled data

18. Wages ( C.I.) 40-60 60-80 80-100 100-120 120-140 140-160
No.of workers
(freq)
50 80 30 20 50 20
X 1 2 3 4 5 Total
No. of Families
(freq)
20 50 20 5 5 100
Problem 1 : Wages (in Rs) paid to workers of an organization are given
below. Calculate Mean, Median and Mode.
Problem 2 : Weekly demand for marine fish (in kg) (x) for 100 families is
given below. Calculate Mean, Median and Mode.
Calculate Mean, Median & Mode

19. In symmetrical
distributions, the median
and mean are equal
For normal distributions,
mean = median = mode
In positively skewed
distributions, the mean is
greater than the median
In negatively skewed
distributions, the mean is
smaller than the median
Relation Between
Mean, Median & Mode

20. •Important Measure of Variation
•Shows Variation About the Mean:
•For the Population:
•For the Sample:
Variance
 
N
Xi
 

2
2


 
1
2
2




n
x
x
s
i
For the Population: use N in the
denominator.
For the Sample : use n - 1 in
the denominator.

21. •Important Measure of Variation
•Shows Variation About the Mean:
•For the Population:
•For the Sample:
Standard Deviation
 
N
Xi
 

2


 
1
2




n
x
x
s
i

22. Coefficient of Variation
Measure of Relative Variation
Always a %
Shows Variation Relative to Mean
Used to Compare 2 or More Groups
Formula (for Sample):
100%








X
SD
CV

23. Stock A: Average Price last year = $50
Standard Deviation = $5
Stock B: Average Price last year = $100
Standard Deviation = $5
Coefficient of Variation:
Stock A: CV = 10%
Stock B: CV = 5%
Comparing Coefficient of Variation

24. Shape of Curve
Describes How Data Are Distributed
Measures of Shape:
Symmetric or skewed
Right-Skewed
Left-Skewed Symmetric
Mean = Median = Mode
Mean Median Mode Median Mean
Mode

25. 1. 5 test scores for Calculus I are 95, 83, 92, 81, 75.
2. Consider this dataset showing the retirement age of
11 people, in whole years:
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
3. Here are a bunch of 10 point quizzes from MAT117:
9, 6, 7, 10, 9, 4, 9, 2, 9, 10, 7, 7, 5, 6, 7
4. 11, 140, 98, 23, 45, 14, 56, 78, 93, 200, 123, 165
Find the Variance, SD & CV

26. Class Interval Frequency
2 -< 4 3
4 -< 6 18
6 -< 8 9
8 -< 10 7
Find the Variance, SD & CV
Example A: 3, 10, 8, 8, 7, 8, 10, 3, 3, 3
Example B: 2, 5, 1, 5, 1, 2
Example C: 5, 7, 9, 1, 7, 5, 0, 4

27. Exam marks for 60 students (marked out of 65)
mean = 30.3 sd = 14.46
Find the Mean, Median, Mode
Variance, SD & CV

28. Group Frequency Table
Frequency Percent
0 but less than 10 4 6.7
10 but less than 20 9 15.0
20 but less than 30 17 28.3
30 but less than 40 15 25.0
40 but less than 50 9 15.0
50 but less than 60 5 8.3
60 or over 1 1.7
Total 60 100.0