Download to read offline
Uploaded byTigabu Yaya
matrixfactorization.ppt
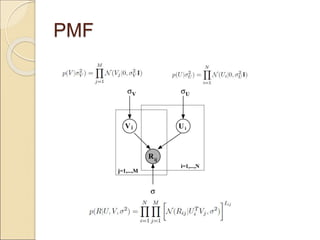
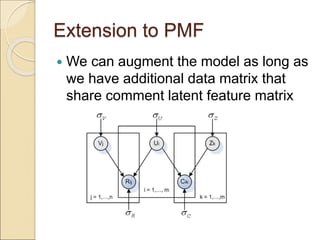
This document discusses different matrix factorization methods and their applications. It covers nonnegative matrix factorization (NMF) and probabilistic matrix factorization (PMF) in more detail. For NMF, it describes using the method to learn the parts of objects from a dataset of facial images. For PMF, it discusses how the technique can be used for recommendation systems by factorizing a user-item rating matrix to predict unknown ratings.
More Related Content
matrixfactorization.ppt
- 1. MAA704: Matrix Analysis NonnegativeMatrix Factorization Presented by: Filmon Tarik Tigabu
- 2. Matrix Factorization andits applications
- 3. Outline Expression powerof matrix Various matrix factorization methods Application of matrix factorization
- 4. Curse of Dimensinality In machine learning and others, Dimension is a curse i.e., as they are intensive computation, and if dimension is high, this will worsen the computation, that’s why we have
- 5. Different matrix factorization methods LU decomposition Singular Value Decomposition(SVD) Probabilistic Matrix Factorization(PMF) Non-negative Matrix Factorization(NMF)
- 6. Application of matrixfactorization LU decomposition ◦ Solving system of equations SVD decomposition ◦ Low rank matrix approximation ◦ Pseudo-inverse
- 7. Application of matrixfactorization PMF ◦ Recommendation system NMF ◦ Learning the parts of objects
- 8. PMF Consider atypical recommendation problem ◦ Given a n by m matrix R with some entries unknown n rows represent n users m columns represent m movies Entry represent the ith user’s rating on the jth movie ◦ We are interested in the unknown entries’ possible values i.e. Predict users’ ratings ij R
- 9. PMF We canmodel the problem as R=U’V ◦ U (k by n) is the latent feature matrix for users How much the user likes action movie? How much the user likes comedy movie? ◦ V (k by m) is the latent feature matrix for movies To what extent is the movie an action movie? To what extent is the movie a comedy movie?
- 10. PMF If wecan learn U and V from existing ratings, then we can compute unknown entries by multiplying these two matrices. Let’s consider a probabilistic approach.
- 11.
- 12. PMF We wantto maximize Equivalent to minimizing Can be solved using steepest descent method
- 13. Extension to PMF We can augment the model as long as we have additional data matrix that share comment latent feature matrix
- 14. NMF Consider thefollowing problem ◦ M = 2429 facial images ◦ Each image of size n = 19 by 19 = 361 ◦ Matrix V = n by m is the original dataset ◦ We want to approximate V by two lower rank matrix W (n by 49) and H (49 by m) V ~ WH Constraints All entries of W and H are non-negative
- 15. NMF How wellcan W and H approximate V How can we interpret the result
- 16. NMF Assumption ◦ ◦ ◦ Maximizelogarithm likelihood and we get the objective function
- 17. Criticize of NMF NMF doesn’t always give parts based result Sparseness constraints For more information, refer to “Non-negative matrix factorization with sparseness constrains”
- 18.