The document outlines an assignment for a Computer Applications for Engineers course at Sokoine University of Agriculture, which involves solving various problems using MATLAB. Each question requires writing specific MATLAB scripts to perform calculations related to fields such as physics, engineering, and mathematics, including topics like system equations, volume calculations, and temperature conversions. The assignment also specifies submission requirements for both hard and electronic copies of the solutions.

1. SOKOINE UNIVERSITY OF AGRICULTURE
FACULTY OF AGRICULTURE
DEPARTMENT OF AGRICULTURAL ENGINEERING AND LAND PLANNING
AE 116 COMPUTER APPLICATIONS FOR ENGINEERS
ASSIGNMENT – MATLAB AND MATLAB APPLICATIONS
SUBMISSION DATE: 30th
JUNE 2017
Name:DOTO,MUSA GESE
IWR/D/2016/0011
INSTRUCTIONS
Attempt the following problems and submit both hard and electronic copies of your solutions
(prepared as one Word document). M-files (and their outputs) should be published in Matlab
and inserted in the Word document to be submitted via email (basalim2000@yahoo.co.uk).
======================================================================
Q1. Write a MATLAB statement to calculate the following equation:
Q2. Using MATLAB, solve the system of the third-order linear algebraic equations given
by Ax = B, where
Q3. For a shell with an external diameter r1 = 10 and internal diameter r2 = 2, write
MATLAB statements to calculate the volume which is given by the following formula:
V = (4/3)π(r1
3
– r2
3
).
Q4. For a shell with an external diameter r1 = 3, 4, 5, 6, 7, 8, 9, and 10 and internal
diameter r2 = 2, write MATLAB statements to calculate and plot a nonlinear function
of the volume, V = f(r1), for the values of r1 given. The volume is given by the
following formula:
V = (4/3)π(r1
3
– r2
3
).
Q5. Write an m-file that will calculate the area of circles (A = πr2
) with radii ranging from 3
to 8 meters at an increment between values entered by the user in the Command
Window. Generate the results in a table using disp and fprintf, with radii in the first
column and areas in the second column. When fprintf is used, print the radii with two
digits after the decimal point and the areas with four digits after the decimal point.

2. Q6. Write an m-file which allows a user to enter a temperature in degrees Fahrenheit and
return the temperature in degrees Kelvin. Use the formulas C = 5(F - 32)/9 and K =
C + 273.15. The output should include both the Fahrenheit and Kelvin temperatures.
Make three variations of the output as:
i. Output temperatures as decimals with 5 digits following the decimal point.
ii. Output temperatures in exponential format with 7 significant digits.
iii. Output temperatures with 4 significant digits.
Q7. A spring’s potential energy is found as E = kx2
/2, where k is the spring constant; x is
the spring displacement. The spring force is F = kx. Using the data for five different
springs as given in Table Q7, write an m-file to find the displacement and potential
energy stored in each spring. Output the results in a table that displays the spring
number, displacement in meters, and potential energy in joules. The calculated
values should have three digits following the decimal point.
Table Q7: Spring data
Spring 1 2 3 4 5
Force (N) 23 123 5 79 8
Spring constant, k 145 33 12 17 34
Q8. The formula for the volume of a truncated cone is
where y is the height; R is the radius of the base; θ is the angle in radians formed by
the centerline and the side of the cone at the ape.
Write an m-file to calculate the volume for radii R = 1, 2, and 3 meters if y = 5 meters
and θ = 20. Calculate three volumes.
Q9. Write an m-file that computes the time t at which an object thrown vertically upward
with the initial velocity v will reach a height h. There are two solutions for t in the
height equation h(t) = vt – (1/2)gt2
because the equation is quadratic. Test the m-file
given the following values: h = 100 m, v = 50 m/sec, and g = 9.81 m/sec2
.
Q10. Electric circuits are described (modelled) using Kirchhoffs voltage and current laws.
Consider an electric circuit described by the following set of five algebraic equations:
R1i1 + R2i2 – v1 = 0
- R2i2+ R3i3+ R5i5 = 0
v2 + R4i4 - R3i3 = 0
- i1 + i2+ i3+ i4 = 0
- i4 - i3 + i5 = 0
i. Write an m-file to calculate the five unknown currents (i1, i2, i3, i4, and i5) given
the following values of resistances and voltages: R1 = 470 Ω, R2 = 300 Ω, R3
= 560 Ω, R4 = 100 Ω, R5 = 1000 Ω, v1 = 5V, and v2 = 10 V. Label the answers
with current number and units.
ii. Using the resistances given above and v1 = 5V, find the range of positive
voltages v2 for which none of the currents exceeds 50 mA. The currents may
be positive or negative. None of the currents may be less than - 50 mA or
greater than 50 mA.
2

3. Q11. The height, horizontal distance, and speed of a projectile launched with a speed v at
an angle A to the horizontal line are given by the following formulas:
The projectile will strike the ground when h(t) = 0, and the time of the hit is
Suppose that A = 30°, v = 40 m/s, and g = 9.81 m/s2
. Use logical operators to find the
times (with the accuracy to the nearest hundredth of a second) when
i. The height is no less than 15 meters.
ii. The height is no less than 15 meters and the speed is no greater than 36
m/sec.
Q12. The horizontal displacement x(t) and vertical displacement y(t) are given with respect
to time, t, as
x(t) = 2t
y(t) = sin(t)
For t = 0 to 10 ms, write a MATLAB script (m-file) to determine the values of x(t) and
y(t) . Use the values to plot x(t) versus y(t) .
Q13. A 3-bit A/D converter, with an analog input x and digital output y, is represented by
the equation:
Write a MATLAB program to convert analog signal x to digital signal y. Test the
program by using an analog signal with the following amplitudes: -1.25, 2.57 and 6.0.
Q14. Write a MATLAB program to determine the number of consecutive integer numbers
which when added together will give a value equal to or just less than 210.
3

4. Q15. For the circuit shown in Figure Q15, use MATLAB to find the nodal voltages V1, V2,
and V3 .
Figure Q15
Q16. For the circuit shown in Figure Q16, use MATLAB to find the current flowing through
the resistor RB and the power supplied by the 10-volt voltage source by using the
mesh analysis method.
Figure Q16
4

5. SOLUTIONs
QN.1
x=1+2-exp (-3) +sin (5);
y=cos (6)-7^-8;
z=x. /y
z =
2.0739
Published with MATLAB® 7.8
QN.2
%Program to solve linear system of equations
%A is 3*3 matrix
%B is the solution of linear equation
%C is the solution of linear equation
A=[1 2 3;4 5 0;6 7 8];
B=[10;20;30];
C=inv(A)*B
C =
-1.6667
5.3333
0.3333
Published with MATLAB® 7.8
QN.3
%program to find volume of cylinder
%r1 is an external diameter
%r2 is an internal diameter
%v is the volume
r1=input('enter internal diameter(r1):');
r2=input('enter external diameter(r2):');
v=(4/3)*pi*(r1.^3-r2.^3)
enter internal diameter(r1):10
enter external diameter(r2):2
v =
4.1553e+003
Published with MATLAB® 7.8
QN.4
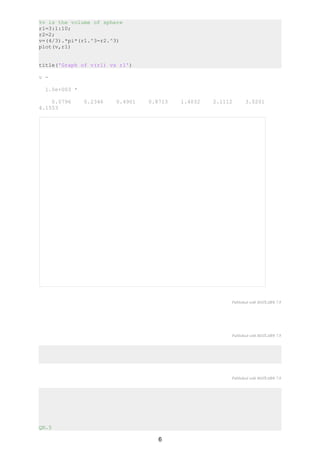
%program to calculate volume of sphere
%r1 is external diameter
%r2 is internal diameter
5

6. %v is the volume of sphere
r1=3:1:10;
r2=2;
v=(4/3).*pi*(r1.^3-r2.^3)
plot(v,r1)
title('Graph of v(r1) vs r1')
v =
1.0e+003 *
0.0796 0.2346 0.4901 0.8713 1.4032 2.1112 3.0201
4.1553
Published with MATLAB® 7.8
Published with MATLAB® 7.8
Published with MATLAB® 7.8
QN.5
6

7. %this program calculate area of circles with ranging from 3 to 8
%an increment is specified by the user
%one table is displayed using disp and other using fprintf
%user input is equal the variable of increment
increment=input('Enter the increment value for the radii:')
%increment radii
r=[3:increment:8];
%equation of the area
A=pi*r.^2;
table1=[r;A];
%transpose table1
table2=table1';
%Disp is used to generate the table
disp('Areas of circle with different radii')
disp('Radius Area')
disp('Meters square meters')
%Transposed table1 printed
disp(table2)
%fprintf is used to generate the table
fprintf('n')
fprintf('Areas of circles with different Radiin')
fprintf('Radius Arean')
fprintf('Meters square Metersn')
fprintf('%5.2f %10.4fn',table1)
%Table automatically transposed
Enter the increment value for the radii:1
increment =
1
Areas of circle with different radii
Radius Area
Meters square meters
3.0000 28.2743
4.0000 50.2655
5.0000 78.5398
6.0000 113.0973
7.0000 153.9380
8.0000 201.0619
Areas of circles with different Radii
Radius Area
Meters square Meters
3.00 28.2743
4.00 50.2655
5.00 78.5398
6.00 113.0973
7.00 153.9380
8.00 201.0619
Published with MATLAB® 7.8
QN.6
%this program allow the user to enter temperature in degree Fahrenheit and
%will return temperature in degree kelvin in three different formats
%user input is equal to the variable "Fahrenheit"
Fahrenheit=input('Enter temperature in degree Fahrenheit:')
%convert from Fahrenheit to Kelvin
Kelvin=5*(Fahrenheit-32)/9+273.15;
fprintf('Kelvin:n')
7

8. %part a: output temperature as decimals with five digits following the
%decimal point
fprintf('%0.5fn',Kelvin)
%part b: output temperature in exponential format with 7 significant digits
fprintf('%0.6en',Kelvin)
%part c: output temperature in general format with 4 significant digits
fprintf('%0.4gnn',Kelvin)
Enter temperature in degree Fahrenheit:100
Fahrenheit =
100
Kelvin:
310.92778
3.109278e+002
310.9
Published with MATLAB® 7.8
Published with MATLAB® 7.8
QN.7
%This program calculate the displacement and potential energy of springs.
%The force and spring constant will be entered by the user for each of five
%springs
%The program will print the output in three columns
%Input the vector value for force and constant"k"
force=[23 123 5 79 8];
k=[145 33 12 17 34];
%Increment spring number
spring_number=[1:1:5];
%calculate displacement
displacement=force./k;
potential=(k.*(displacement.^2))/2;
%calculate potential energy stored in spring
%Table of values
table=[spring_number;displacement;potential];
fprintf('spring Number Displacement Potential Energyn')
fprintf(' (meters) (Joules)n')
%print output
fprintf('%1.0f %7.3f %7.3fn',table)
8

9. spring Number Displacement Potential Energy
(meters) (Joules)
1 0.159 1.824
2 3.727 229.227
3 0.417 1.042
4 4.647 183.559
5 0.235 0.941
Published with MATLAB® 7.8
QN.8
%This program calculate volume of a truncated cone after the user inputs
%cone height
%radius of the base,and the angle in radians formed bu the centreline and
%the side of the cone at the apex
%prompt user to input data,input asigned to the specified variable names
y=input('Enter the height of the cone in meters:n')
R=input('enter the three radii in meters:n')
t=input('Enter the angle in degrees:n')
%Convert angles from degrees to radians
t=t*pi/180;
%calculate volume for the three radii
v=((pi*R.^3)/(3*tan(t)))-(pi/3)*((R-y*tan(t)).^2).*((R./(tan(t)))-y);
%Display calculated output for the three radii
disp('The three volumes are found to be')
disp(v)
Enter the height of the cone in meters:
5
y =
5
enter the three radii in meters:
[1 2 3]
R =
1 2 3
Enter the angle in degrees:
20
t =
20
The three volumes are found to be
4.4627 23.0004 72.9541
Published with MATLAB® 7.8
QN. 9
%program to calculate time at which the object thrown the vertically upward
%H is the height of the object vertically upward
%v is upward velocity of the object
%g is the acceralation due to gravity
%time calculated when the user input values of H,v and g
h=input('Enter height h:');
v=input('Enter veloccity v:');
g=input('Enter acceralation due to gravity g:');
if v.^2>2.*g.*h
9

10. t1=(v+sqrt(v.^2-2.*g.*h))/g;
t2=(v-sqrt(v.^2-2.*g.*h))/g;
fprintf('The value of t1 is %f secn',t1);
fprintf('The value of t2 is %f secn',t2);
else
fprintf('roots of equation are complexn');
end
Enter height h:100
Enter veloccity v:50
Enter acceralation due to gravity g:9.81
The value of t1 is 7.461246 sec
The value of t2 is 2.732434 sec
Published with MATLAB® 7.8
QN.10
%program to calculates the value of five currents using kirchhoff's
%voltage law
%part A.variable values
R1=470;R2=330;R3=560;R4=100;R5=1000;V1=5;V2=10;
%matrices used to solve the equation
A=[R1 R2 0 0 0;0 -R2 R3 0 R5;0 0 -R3 R4 0;-1 1 1 1 0; 0 0 -1 -1 1];
B=[V1;0;-V2;0;0];
%vector for the current number
I=[1:5];
%solve the linear algebraic equation
C=(AB)';
%create a table to output current number and current value
table=[I;C];
%print a table to output the currrent values
fprintf('Part A:n')
fprintf('current Number current valuen')
fprintf(' (amperes)n')
fprintf('------ -------n')
fprintf('%4.0f %8.6fn',table)
%part B
%form a loop to find the range of positive voltages V2(current cannot)
%exceed 0.05A value of subscript n
n=1;
%use a range of V2 between 0V and 30V,incrementing by 0.1
%the absolute value of current (vector C) is used to avoid 2 loops
%subscript n is incremented by 1
for V2=0:0.1:30
B=[V1;0;-V2;0;0];
C=AB;
if abs(C)<0.05
V(n)=V2;
n=n+1;
end
end
%find minimum and maximum of V2 and assign to two varibles
V_max=max(V);
V_min=min(V);
%print the output
fprintf('nnPart B:n')
fprintf('The range of voltage V2 for which no current are bellown')
fprintf('-50mA or above 50mA is %4.1f V to %4.1f V.nn',V_min,V_max)
Part A:
current Number current value
(amperes)
------ -------
1 0.004178
2 0.009201
3 0.014391
4 -0.019413
10

11. 5 -0.005022
Part B:nThe range of voltage V2 for which no current are bellow
-50mA or above 50mA is 0.0 V to 24.7 V.
Published with MATLAB® 7.8
QN.11
%This program find the times at which the conditions specified bellow are
%satisfied parameters
A=30;v0=40;g=9.81;
%Part i:Determine the times at which the height is no less than 15 meters.
%Increment time by 0.01
time=[0:0.01:5];
%Find height (h) for different values of time
h=v0.*sin(A*pi/180)-0.5*g*time.^2;
%Determine times when height is greater than 15 meters
times=find(h>=15);
%Find the maximmum and minimum value for times
max_time=max(times)/100;
min_time=min(times)/100;
%Print the results
fprintf('nThe height is atleaast 15m when the time is betweenn')
fprintf(' %.2fseconds and %.2fseconds.nn',min_time,max_time)
%Part ii:determine t at which h is now less than 15m and vis no more than
%36m/sec
%Increment time by 0.01
time=[1:0.01:5];
%Find height (h)and velocity (v) for different values of time
h=v0*time.*sin(A*pi/180)-0.5*g*time.^2;
v=sqrt((v0^2)-(2*v0*g.*sin(A*pi/180))+(g^2*time.^2));
%Determine time when height is greater than 15m and velocity is more than
%36m/sec
vector=find(h>15&v<=36);
%Find the maximum and minimum value for times
max_time=max(times);
min_time=min(times);
%Print the results
fprintf('nnThe height is atleast 15m and velocity is no less than
36m/sn')
fprintf('when time is between %f seconds and %f
seconds.nn',min_time,max_time)
The height is atleaast 15m when the time is between
0.01seconds and 1.01seconds.
The height is atleast 15m and velocity is no less than 36m/s
when time is between 1.000000 seconds and 101.000000 seconds.
Published with MATLAB®
QN.12
%x(t) is horizontal displacement
%y(t) is vertical displacement
%t is time in millisecond(ms)
fprintf('x(t) y(t)n')
for t=0:0.5:10;
11

12. x=2.*t;
y=sin(t);
fprintf('%8.0f %8.4n',x,y)
end
%plot graph of x(t) versus y(t)
t=0:0.5:10;
x=2.*t
y=sin(t);
plot(x,y);
title('Graph of x(t) VS y(t)')
x(t) y(t)
0 1 2 3 4 5 6 7
8 9 10 11 12 13 14 15 16
17 18 19 20
x =
Columns 1 through 16
0 1 2 3 4 5 6 7 8 9 10 11
12 13 14 15
Columns 17 through 21
16 17 18 19 20
Published with MATLAB® 7.
QN.13
%program of obtaining Y_dig given X_analog
%Y_dig is the digital number(in interger form)
%X_analog is the analog input(in decimal form)
X_analog=input('Enter analogue signal X:')
if X_analog<-2.5
fprintf('Y_digital=0;n');
elseif X_analog>=-2.5&X_analog<-1.5
12

13. fprintf('Y_digita=l;n');
elseif X_analog>=-1.5&X_analog<-0.5
fprintf('Y_digital=2;n');
elseif X_analog>=-0.5&X_analog<0.5
fprintf('Y_digital=3;n');
elseif X_analog>=0.5&X_analog<1.5
fprintf('Y_digital=4;n');
elseif X_analog>=1.5&X_analog<2.5
fprintf('Y_digital=5;n');
elseif X_analog>=2.5&X_analog<3.5
fprintf('Y_digital=6;n');
else
fprintf('Y_digital=7;n');
end
Enter analogue signal X:-1.25
X_analog =
-1.2500
Y_digital=2;
Enter analogue signal X:2.57
X_analog =
2.57
Y_digital=6;
Enter analogue signal X:6
X_analog =
Y_digital=7;
Published with MATLAB® 7.8
QN.14
%interger summation
%int is an interger
%max_val is maximum value of interger
%int_sum is interger sum
%num_int is last interger
%tt_int_ct is total interger count
int=1;int_sum=0;
max_val=210;
while int_sum<max_val
int_sum=int_sum+int;
int=int+1;
end
last_int=int
if int_sum==max_val
num_int=int-1
tt_int_ct=int sum
elseif int_sum>max_val
num_int=int-1
tt_int_ct=int_sum-last_int
end
last_int=21
num_int=20
tt_inc_ct=210
Published with MATLAB® 7.8
13

14. QN.15
A=[3 -2 -1; 200 -290 50;2 1 -3];
B=[100;0;-80];
fprintf('Nodal voltage V1,V2 and V3 aren')
V=inv(A)*B
fprintf('respectivelyn')
Nodal voltage V1,V2 and V3 are
V =
404.2857
350.0000
412.8571
respectively
Published with MATLAB® 7.8
QN16
%this program determines the current
%flowing in a resistor RB and power supplied bby source
%it computes the loop current given the impedance
%matrix Z and voltage vector V
%initialize the matrix Zand vector V
Z=[40 -10 -30;-10 30 -5;-30 -5 65];
V=[10 0 0]';
%solve the loop currents
I=inv(Z)*V
%current through RBis calculated
IRB=I(1)-I(2);
fprintf('the current through R is %8.3Ampsn',IRB)
%the power supplied by the source is calculated
PS=I(1)*10;
fprintf('the power supplied by 10V sourceis %8.4f wattsn',PS)
the current through R is 0.037
the power supplied by 10V source is 4.7531 watts
Published with MATLAB® 7.8
14