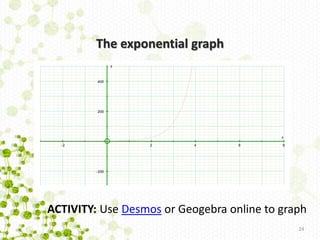
This document summarizes a study on designing and delivering a continuing professional development (CPD) course on mathematics for A-level Biology. It involved biology teachers in designing the course content on exponentials/logarithms and statistics. The day was delivered to 20-30 teachers. Data was collected on the impact on teachers' math confidence and teaching practice. Preliminary findings showed the design process improved math teaching confidence and the day further increased statistics confidence while providing pedagogical support ideas. Challenges included time away from school and differing research/practice cultures.

1. Maths for Biology
January 9th 2016 ASE
Carys Hughes
Christian Bokhove
Hilary Otter
Rebecca D’Silva
Nicky Miller

2. Introductions
• Carys Hughes
• Christian Bokhove
• Hilary Otter
• Rebecca D’Silva
• Nicky Miller

3. This study
• Design a CPD course on Maths for A level
Biology
• Involve teachers in its design
• Implement the day
• Evaluate impact of the two groups of teachers.

4. Why this day
• Changes in the A level Biology curriculum
• More maths
• Maths used interdisciplinary
• Principles
– Instruction but also hands-on tasks
– Collaborative, doing it together, ask questions
– Want to customise the course to where you need
support

5. Part I: designing the day (process)
• Communities of Interest and Boundary Objects
• Involve three Biology teachers, and two researchers, one
Maths, one Biology
• Two development sessions of 2 hours
• All the teachers’ contributions will be recorded through notes
and audio.
• After delivery of the day teachers interviewed in a group
interview/focus group.
Research questions:
• In what way can these teachers contribute to the design of the
delivered session?
• What impact does the involvement in the design process have
on their own professional development.

6. Part 2: delivery of the CPD day (product)
• 20-30 teachers
• Whole day, free
• Focus on exponentials/logarithms and statistics
(came from the design part with teachers)
• Data collection: maths confidence, evaluation,
impact
Research question:
• What impact does a CPD day on maths for the new
Biology A-level curriculum have on participant’s
maths confidence and teaching practice?

7. • Update and strengthen knowledge on some
topics for the new Biology A level curriculum;
– Exponential growth and decay, logarithms
– Statistical tests
• Hear and discuss ideas for teaching them;
• Want to hear your opinions for improvements;
• You leave with:
– Ideas, knowledge and some resources

8. Example of data collection
Focus group questions
• What, in your view, did you manage to contribute to the design of the CPD
session?
• What impact, in your opinion, did the involvement in the design process
have on their own professional development.
– Did have an impact on your confidence in teaching Biology?
– And the maths component in particular? (engagement, confidence,
liking, valuing)
• What impact, in your opinion, did the participation in the whole project
(including the actual CPD day) have on their own professional development.
– Did have an impact on your confidence in teaching Biology?
– And the maths component in particular? (engagement, confidence,
liking, valuing)
• Did you feel the whole process has had an impact on students?
– Engagement with maths? Confidence in maths? Liking maths?
– Valuing maths?

9. Example of data collection
modified Fennema-Sherman Attitude Scales

10. Tentative findings: process
• Usefulness of the Community of Interest
• Knowledge acquisition
• Improved confidence in teaching the maths in A
level biology
• Better understanding of the processes involved
in the calculations

11. Tentative findings: product/day
• Valued content exponentials/logarithms
• More confident statistics but worthwhile to
compare and discuss pedagogy
• On confidence:
– They think they can learn maths
– They think it's important and worthwhile
– They need maths for their work
– But it's hard!
– So need support.

12. Challenges
• Getting teachers away from school for CPD
– Design phase twilight
– Day was free
– After A-level exams
• Data collection
• Culture clash
– Research v Practice
– Maths v Science

13. Taster from
the CPD day

14. Powers and
exponential

15. Slide exam curriculum
From (i) A.0 - arithmetic and numerical
computation
A.0.5 Use calculators to find and use power, exponential
and logarithmic functions Candidates may be tested on their
ability to: estimate the number of bacteria grown over a
certain length of time
From (ii) A.2 – algebra
A.2.5 Use logarithms in relation to quantities that range
over several orders of magnitude Candidates may be tested
on their ability to: use a logarithmic scale in the context of
microbiology, e.g. growth rate of a microorganism such as
yeast

16. Powers of 10
Movie on youtube
ThereisanewerversioncalledCosmicVoyage,narratedby
MorganFreeman.It,however,doesnothavethestandard
notationincluded.

17. 17
ACTIVITY
Exponentials
Take an A4 sheet of paper.
How many times can you fold it in half?

18. MYTHBUSTERS
Movie on youtube

19. 19
How many layers do you produce? HANDOUT
Number
of folds
(x)
Number
of layers
(y)
Mult Power Heig
ht
(cm)
0 1 0.01
1 2 2
2 2*2
3 2*2*2
4 2*2*2*2 24
5
Table of results
H

20. 20
Plot your values on graph paper:
- 3 - 2 - 1 1 2 3 4 5 6 7 8
- 100
100
200
300
x
y
- 3 - 2 - 1 1 2 3 4 5 6 7 8
- 100
100
200
300
x
y

21. 21
Exponential growth
Imagine you contracted a virus (such as SARS)
where you infected the first five people that
you met, and they each infected the first five
people that they met and so on…. There are
186,701 people living in Southampton. How
many interactions would it take until everyone
was infected?

22. 22
How many infections?
Number of interactions
(x)
Number of infected
people (y)
0 1
1 5
2 25
3
4
5
Table of results

23. 23
General form:
y=bt
where b is the base and x is the power (or exponent)

24. 24
The exponential graph
- 2 2 4 6 8
- 200
200
400
x
y
ACTIVITY: Use Desmos or Geogebra online to graph

25. 25
How many layers do you produce?
Number
of folds
(x)
Number
of layers
(y)
Heig
ht
(cm)
0 1 0.01
1 2 2
2 2*2
3 2*2*2
4 2*2*2*2 24
5
Table of results
y=2x

26. 26
Common features of y=bx
all curves pass through (0,1)
exponential growth (and decay) takes
place very rapidly
b > 0
b 0
b 1
b > 1 has a positive gradient (PLOT THIS!)
0 < b < 1 has a negative gradient (PLOT THIS!)


https://www.desmos.com/calculator/auubsaje
fh

27. Number of
interactions (x)
Number of people with the
disease (y)
0 1
1 5
2 25
3 125
4 625
5 3,125
6 15,625
7 78,125
8 390,625

28. Statistics

29. Slide exam curriculum
From (i) A.1 - handling data
A.1.9 Select and use a statistical test Candidates may
be tested on their ability to select and use:
• the Chi squared test to test the significance of the
difference between observed and expected results
• the Students t-test
• the correlation coefficient
A.1.11 Identify uncertainties in measurements and use
simple techniques to determine uncertainty when data are
combined Candidates may be tested on their ability to:
• calculate percentage error where there are uncertainties
in measurement

30. Statistical tests
• Type of data collected
– Measurements
– Frequencies
• What are you looking for?
– Associations
– Differences
(Source: TES site)

31. (Source: TES site)

32. Conclusion
• CPD day designed by Community of Interest for
Biology teachers
• Improvement maths confidence
• Now writing up the study
• Questions?
• Thank you for your
attention.
http://is.gd/maths4bio