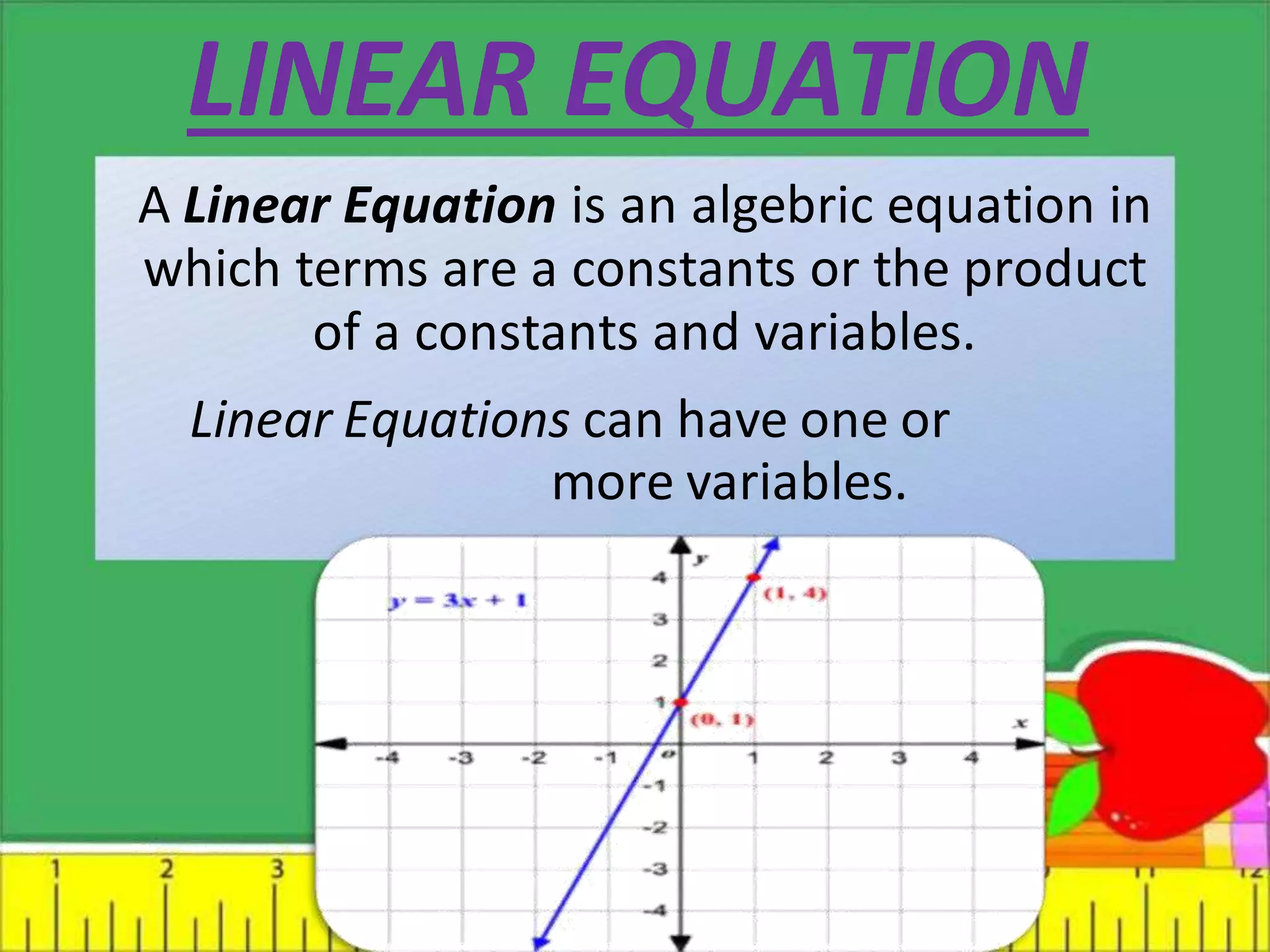
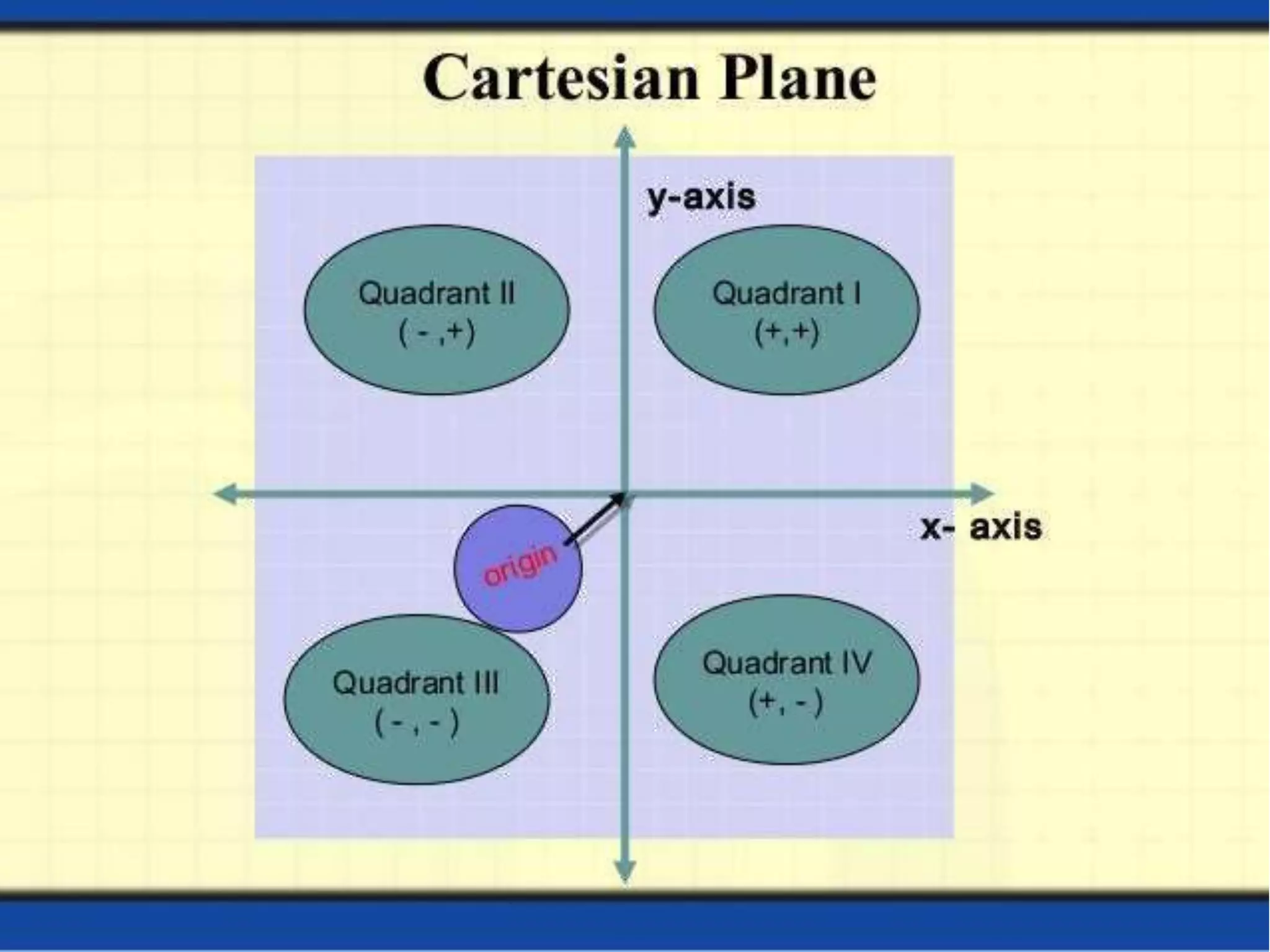
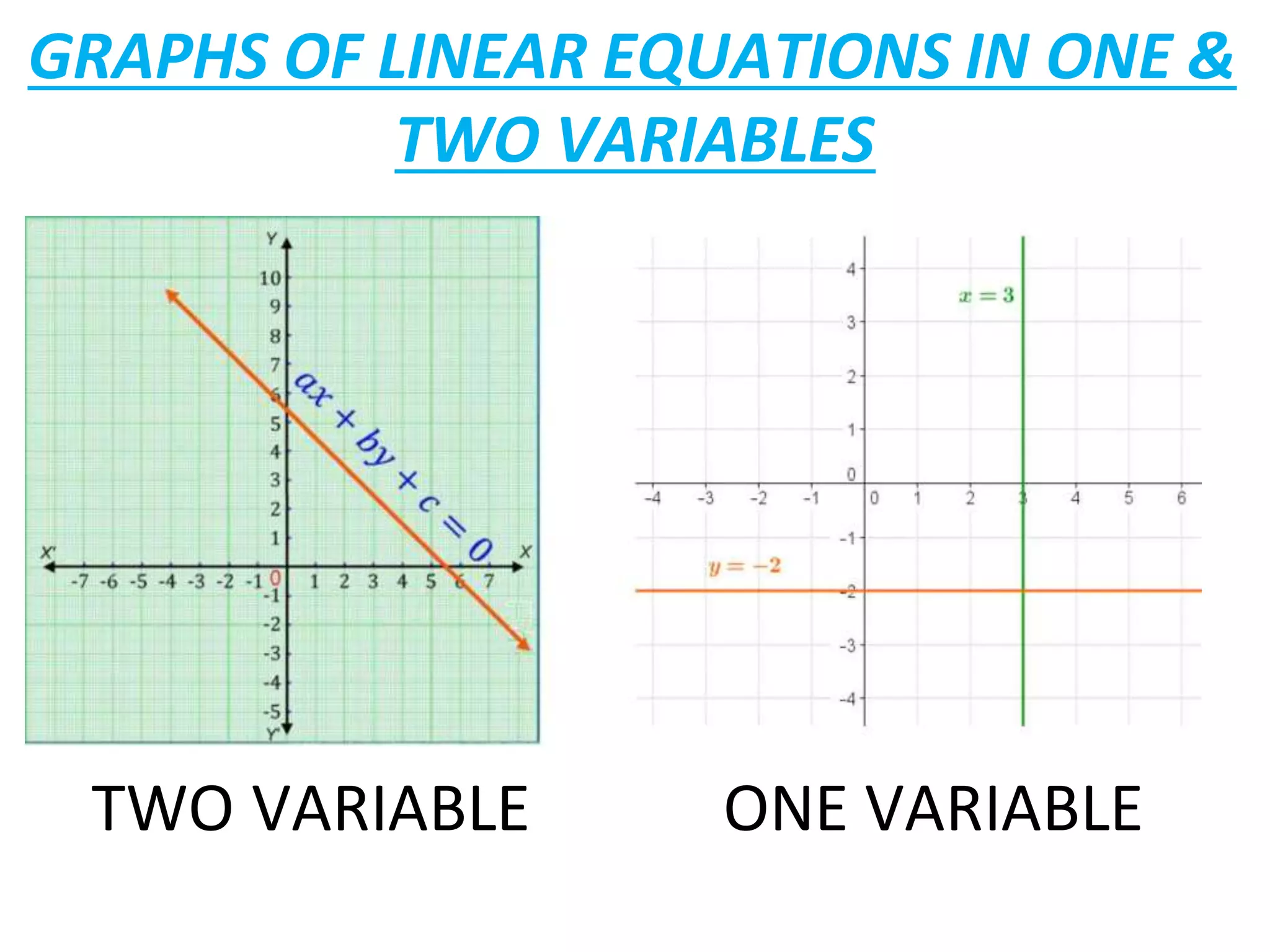
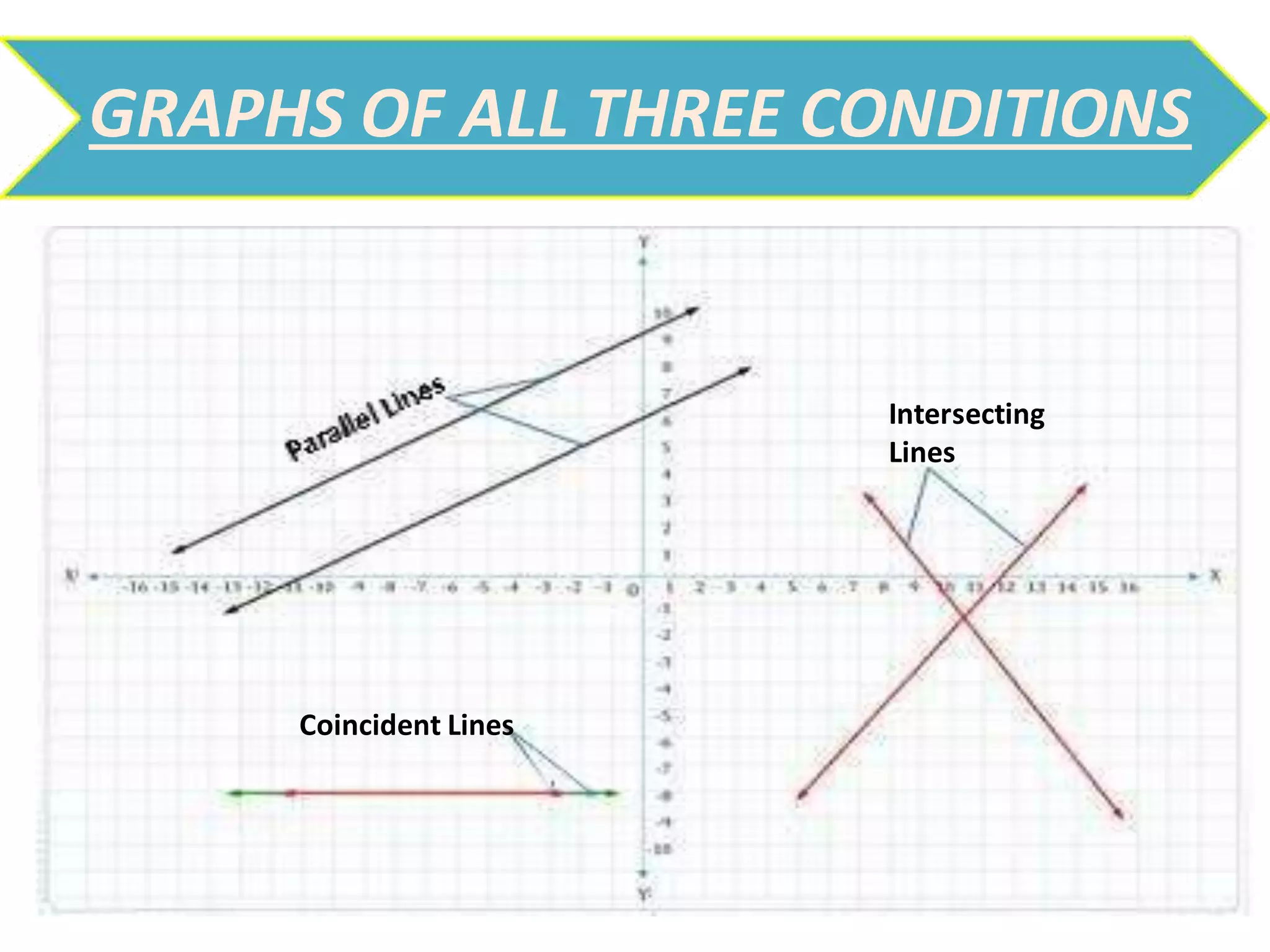
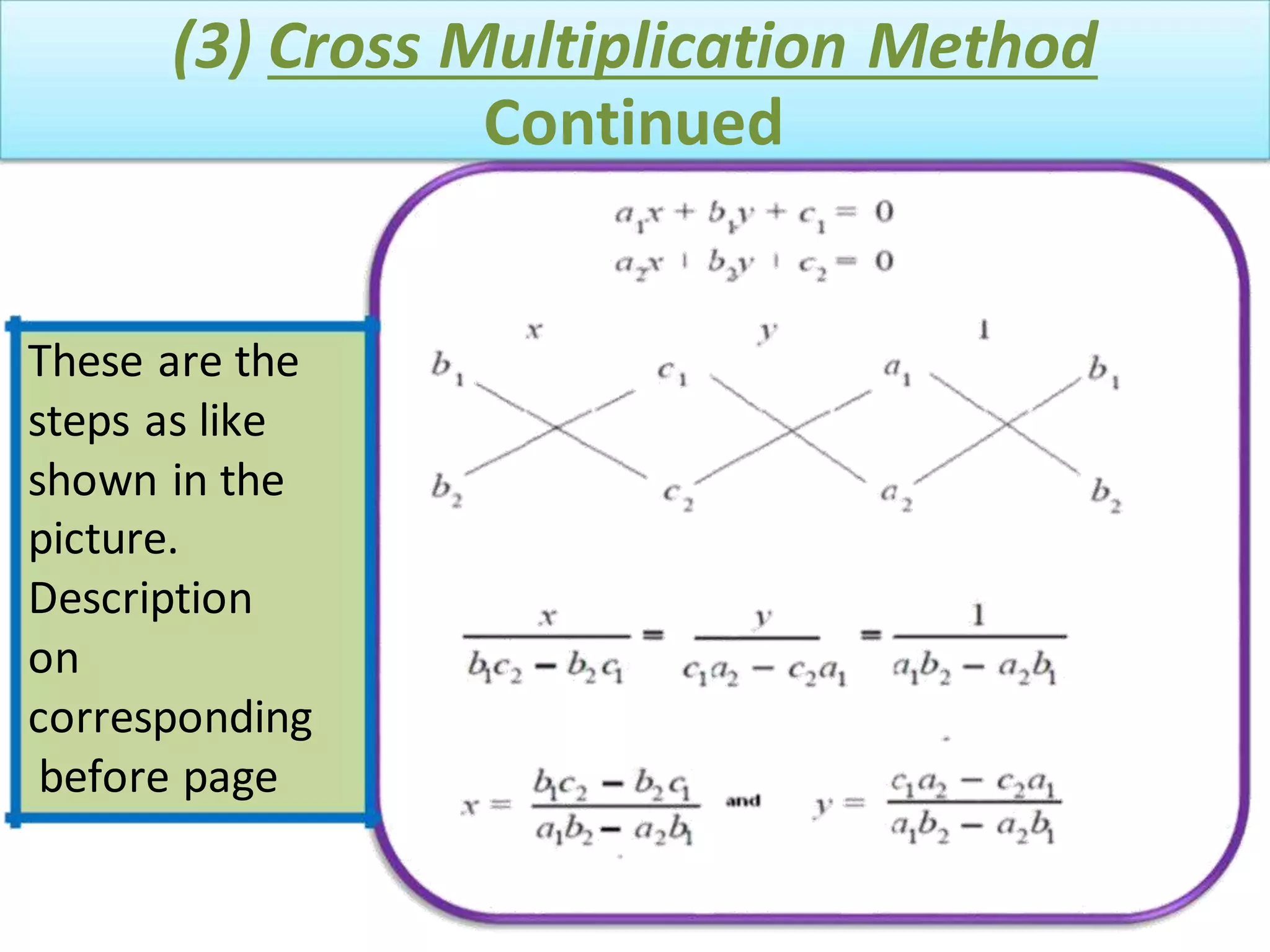
Linear equations are algebraic equations where terms are constants or products of constants and variables. There are two main types: equations with one variable and equations with two variables. There are three main methods to solve a pair of linear equations with two variables: 1) the graphical method involves plotting the lines defined by each equation and finding their point(s) of intersection, 2) the algebraic elimination method involves manipulating the equations to eliminate one variable, and 3) the cross-multiplication method sets up the equations in a fraction format and cross-multiplies the variables and coefficients. Examples are shown for each solving method.

2. LINEAR EQUATION
A Linear Equation is an algebric equation in
which terms are a constants or the product
of a constants and variables.
Linear Equations can have one or
more variables.

4. LINEAR EQUATIONS IN TWO
VARIABLES
The equations ax + by – c = 0 ,
which can be where a & b
written in the both can never
form-> be 0
These type Examples ->
equations are •47x + 7y = 9
called Linear •73a – 61b = – 13
Equations In •44u + 10v – 155 = 0
Two Variable . •30p + 100 q = 0

5. GRAPHS OF LINEAR EQUATIONS IN ONE &
TWO VARIABLES
TWO VARIABLE ONE VARIABLE

6. PAIR OF LINEAR EQUATIONS IN TWO
VARIABLES
Each linear equation in two variables defined a straight
line. To solve a system of two linear equations in two
variables, we graph both equations in the same
coordinate system. The coordinates of any points that
graphs have in common are solutions to the system,
since they satisfy both equations. The general form of a
pair of linear equations in two variables x and y as
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
where a1, a2, b1, b2, c1, c2 are all real numbers and
a1
2
+ b1
2
≠ 0 and a2
2
+ b2
2
≠ 0.

7. METHODS FOR SOLVING
PAIR OF LINEAR EQUATIONS
IN TWO VARIABLES
There are two methods for solving PAIR OF
LINEAR EQUATIONS IN TWO VARIABLES

(1) GRAPHICAL Method
(2) ALGEBRAIC Method

8. GRAPHICAL METHOD FOR SOLVING
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
When a pair of linear equations is plotted, two lines are defined. Now,
there are two lines in a plane can intersect each other, be parallel to each
other, or coincide with each other. The points where the two lines
intersect are called the solutions of the pair of linear equations.
Condition 1: Intersecting Lines
If a1/a2 ≠ b1/b2, then the pairof linearequationsa1x+ b1y + c1 = 0, a2x+ b2y + c2 = 0 has a
uniquesolution.
Condition 2: Coincident Lines
If a1/a2 = b1/b2 = c1/c2, then the pairof linearequationsa1x + b1y + c1 = 0, a2x + b2y + c2 = 0
has infinitesolutions.
Condition 3: Parallel Lines
If a1/a2 = b1/b2 ≠ c1/c2, then a pair of linear equations a1x + b1y + c1 = 0, a2x + b2y + c2 =
0 has no solution.
A pair of linear equations which has no solution is said to be an Inconsistent
pair of linear equations.A pair of linear equations, which has a unique or
infinite solutions are said to be a Consistentpair of linear equations.

9. GRAPHS OF ALL THREE CONDITIONS
Intersecting
Lines
Coincident Lines

10. ALGEBRAIC METHOD FOR SOLVING
PAIR OF LINEAR EQUATIONS IN
TWO VARIABLES
There are three Algebraic Methods for solving PAIR
OF LINEAR EQUATIONS IN TWO VARIABLES

1. Elimination by Substitution Method
2. Elimination by Equating Coefficient Method
3. Cross Multiplication Method

11. (1) Elimination by Substitution
Method
Steps

1. The first step for solving a pair of linear equations by the
substitution method is to solve one equation for either
of the variables.
2. Choosing any equation & any variable for the first step
does not affect the solution for the pair of equations .
3. In the next step, we’ll put the resultant value of the
chosen variable obtained in the chosen equation in
another equation and solve for the other variable.
4. In the last step, we can substitute the value obtained of
one variable in any one equation to find the value of the
other variable.

12. (2) Elimination by Equating Coefficient
Method
Steps

1. Equate the non-zero constants of any variable by
multiplying the constants of a same variable in both
equations with other equation, so that the
resultant constants of one variable in both
equations become equal.
2. Subtract one equation from another, to eliminate
a variable and find the value of that variable
3. Solve for the remaining variable by putting the
value of one solved variable .

13. (3) Cross Multiplication Method
1)) Let’s consider the general form of a pair of linear
equations a1x + b1y + c1 = 0 , and a2x + b2y + c2 = 0.
2)) To solve the pair of equations for x and y using cross-
multiplication, we’ll arrangethe variables x and y and their
coefficients a1, a2, b1 and b2, and the constants c1 and c2 as
shown below
x / (b1*c2-b2*c1) = y / (c1*a2- c2*a1) = 1 / (a1*b2-a2*b1)
3)) Now simplifying the above situation, and putting the values of
x with 1 & y with 1 to find the value of x & y

14. (3) Cross Multiplication Method
Continued
These are the
steps as like
shown in the
picture.
Description
on
corresponding
before page

15. EXAMPLES
Elimination by Substitution
Method

16. Elimination by Equating Coefficient
Method

17. CROSS MULTIPLICATION METHOD

18. Prepared By

MUKUL SAXENA
Roll No.

30
Class X ‘D’
Submitted To

Mr. S.K. JHA Sir