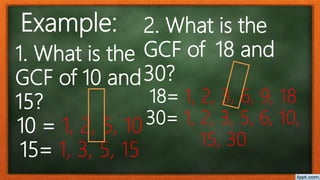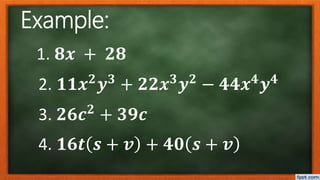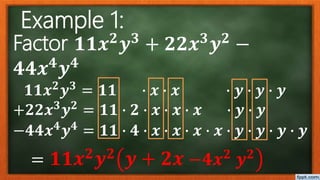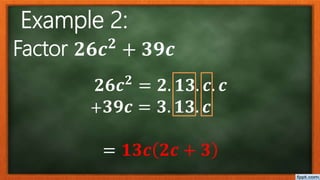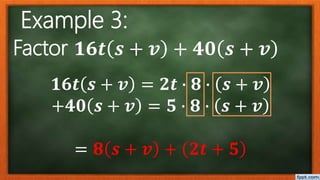This document discusses factoring polynomials with common factors. It defines a factor as a number that divides another number without a remainder. The greatest common factor (GCF) is the largest factor common to two or more numbers. The document provides examples of finding the GCF of various numbers and polynomial terms. It explains that a polynomial is an expression involving variables and coefficients using addition, subtraction, multiplication, and exponents. The document outlines the steps to factor polynomials by finding the GCF of coefficients, identifying common variables, dividing each term by the GCF, and writing the factored form. It provides examples of factoring different polynomials.

1. Polynomial
Dissection
CHAPTER 1

2. Factoring
Polynomials with a
Common Factor

3. What is a Factor?
A factor is one of two or
more numbers that
divides a given number
without a remainder.

4. Example:
What are the factors of 10?
1, 2, 5, 10
What are the factors of 20?
1, 2, 4, 5, 10, 20

5. What is a GCF?
A GCF (Greatest
Common Factor) is the
greatest factor that is
common to two or

6. 1. What is the
GCF of 10 and
15?
10 = 1, 2, 5, 10
15= 1, 3, 5, 15
2. What is the
GCF of 18 and
30?
18= 1, 2, 3, 6, 9, 18
30= 1, 2, 3, 5, 6, 10,
15, 30
Example:

7. 3. What is the GCF of
𝟏𝟒𝒃 𝟐
, 𝟐𝟖𝒃 and 𝟑𝟓𝒃 𝟑
?
𝟏𝟒𝒃 𝟐
= 𝟐 ∙ 𝟕 ∙ 𝒃 ∙ 𝒃
𝟐𝟖𝒃 = 𝟐 ∙ 𝟐 ∙ 𝟕 ∙ 𝒃
𝟑𝟓𝒃 𝟑
= 𝟓 ∙ 𝟕 ∙ 𝒃 ∙ 𝒃 ∙ 𝒃
𝑮𝑪𝑭 = 𝟕𝒃
Example:

8. A Polynomial is an expression
consisting of variables and
coefficients, that involves only the
operations of addition, subtraction,
multiplication, and non-negative
integer exponentiation of variables.
What is Polynomial?

9. 1. 𝟖𝒙 + 𝟐𝟖
Example:
2. 𝟏𝟏𝒙 𝟐
𝒚 𝟑
+ 𝟐𝟐𝒙 𝟑
𝒚 𝟐
− 𝟒𝟒𝒙 𝟒
𝒚 𝟒
3. 𝟐𝟔𝒄 𝟐
+ 𝟑𝟗𝒄
4. 𝟏𝟔𝒕 𝒔 + 𝒗 + 𝟒𝟎 𝒔 + 𝒗

10. 1. 𝑴𝒐𝒏𝒐𝒎𝒊𝒂𝒍
Types of Polynomials
2. 𝑩𝒊𝒏𝒐𝒎𝒊𝒂𝒍
3. 𝑻𝒓𝒊𝒏𝒐𝒎𝒊𝒂𝒍
4. 𝑴𝒖𝒍𝒕𝒊𝒏𝒐𝒎𝒊𝒂𝒍

11. How to factor polynomials with
a common factor?
Factoring is the reverse of
multiplication.The Distributive Property is used to
factor out the GCF of the terms in a
polynomial and to write the
polynomial in factored form.

12. The Distributive Property states
that
𝑎𝑏 + 𝑎𝑐 = 𝑎 𝑏 + 𝑐
Example:
8𝑥 + 28
4 ∙ 2𝑥 + 4 ∙ 7
𝟒 𝟐𝒙 + 𝟕
Find the GCF of 8 and 28.
The GCF of 8 and 28 is 4.


13. STEPS IN FACTORING
POLYNOMIALS1. Find the GCF of the numerical
coefficients.
2. Check the variable which appears in all
the terms. If a variable appears in all
the terms, choose the lowest degree
for each variable.
3. Divide each term by the GCF.
4. Write the factored form.

14. Factor 𝟏𝟏𝒙 𝟐
𝒚 𝟑
+ 𝟐𝟐𝒙 𝟑
𝒚 𝟐
−
𝟒𝟒𝒙 𝟒
𝒚 𝟒
𝟏𝟏𝒙 𝟐 𝒚 𝟑 = 𝟏𝟏 ∙ 𝒙 ∙ 𝒙 ∙ 𝒚 ∙ 𝒚 ∙ 𝒚
+𝟐𝟐𝒙 𝟑 𝒚 𝟐 = 𝟏𝟏 ∙ 𝟐 ∙ 𝒙 ∙ 𝒙 ∙ 𝒙 ∙ 𝒚 ∙ 𝒚
−𝟒𝟒𝒙 𝟒 𝒚 𝟒 = 𝟏𝟏 ∙ 𝟒 ∙ 𝒙 ∙ 𝒙 ∙ 𝒙 ∙ 𝒙 ∙ 𝒚 ∙ 𝒚 ∙ 𝒚 ∙ 𝒚
Example 1:
= 𝟏𝟏𝒙 𝟐 𝒚 𝟐 𝒚 + 𝟐𝒙 −𝟒𝒙 𝟐
𝒚 𝟐

15. Factor 𝟐𝟔𝒄 𝟐
+ 𝟑𝟗𝒄
𝟐𝟔𝒄 𝟐
= 𝟐. 𝟏𝟑. 𝒄. 𝒄
+ 𝟑𝟗𝒄 = 𝟑. 𝟏𝟑. 𝒄
= 𝟏𝟑𝒄 𝟐𝒄 + 𝟑
Example 2:

16. Factor 𝟏𝟔𝒕 𝒔 + 𝒗 + 𝟒𝟎 𝒔 + 𝒗
𝟏𝟔𝒕 𝒔 + 𝒗 = 𝟐𝒕 ∙ 𝟖 ∙ 𝒔 + 𝒗
+𝟒𝟎 𝒔 + 𝒗 = 𝟓 ∙ 𝟖 ∙ 𝒔 + 𝒗
= 𝟖 𝒔 + 𝒗 + 𝟐𝒕 + 𝟓
Example 3: