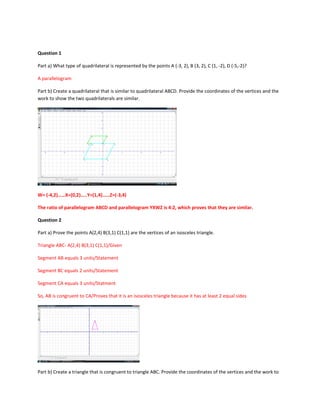
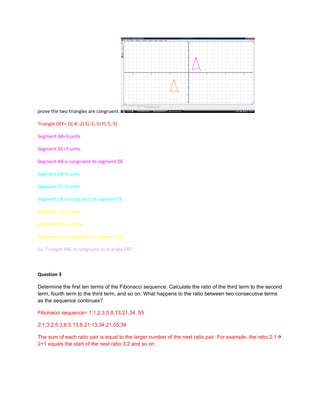
The document contains solutions to 3 math problems: 1) Identifying a quadrilateral with given vertices as a parallelogram and creating a similar quadrilateral. 2) Proving a triangle with given vertices is isosceles and creating a congruent triangle. 3) Calculating the first 10 terms of the Fibonacci sequence and noting the ratios between consecutive terms approach a constant.

1. Question 1
Part a) What type of quadrilateral is represented by the points A (-3, 2), B (3, 2), C (1, -2), D (-5,-2)?
A parallelogram
Part b) Create a quadrilateral that is similar to quadrilateral ABCD. Provide the coordinates of the vertices and the
work to show the two quadrilaterals are similar.
W= (-4,2)……X=(0,2)…..Y=(1,4)……Z=(-3,4)
The ratio of parallelogram ABCD and parallelogram YXWZ is 4:2, which proves that they are similar.
Question 2
Part a) Prove the points A(2,4) B(3,1) C(1,1) are the vertices of an isosceles triangle.
Triangle ABC- A(2,4) B(3,1) C(1,1)/Given
Segment AB equals 3 units/Statement
Segment BC equals 2 units/Statement
Segment CA equals 3 units/Statment
So, AB is congruent to CA/Proves that it is an isosceles triangle because it has at least 2 equal sides
Part b) Create a triangle that is congruent to triangle ABC. Provide the coordinates of the vertices and the work to

2. prove the two triangles are congruent.
Triangle DEF= D(-4,-2) E(-3,-5) F(-5,-5)
Segment AB=3 units
Segment DE=3 units
Segment AB is congruent to segment DE
Segment CB=2 units
Segment FE=2 units
Segment CB is congruent to segment FE
Segment CA=3 units
Segment FD= 3 units
Segment CA is congruent to segment FD
So, Triangle ABC is congruent to triangle DEF
Question 3
Determine the first ten terms of the Fibonacci sequence. Calculate the ratio of the third term to the second
term, fourth term to the third term, and so on. What happens to the ratio between two consecutive terms
as the sequence continues?
Fibonacci sequence= 1,1,2,3,5,8,13,21,34, 55
2:1,3:2,5:3,8:5,13:8,21:13,34:21,55:34
The sum of each ratio pair is equal to the larger number of the next ratio pair. For example, the ratio 2:1à
2+1 equals the start of the next ratio 3:2 and so on…