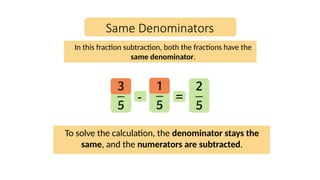
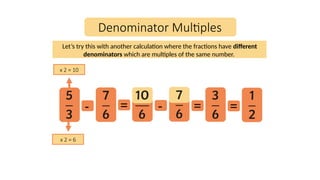
The document explains how to convert mixed numbers to improper fractions by multiplying the whole number by the denominator and adding the numerator. It also covers the process of subtracting fractions, both with the same denominator and with different denominators that are multiples of a common number. Additionally, several worked examples illustrate these concepts.

2. 13
5
2
3
5
Mixed Numbers
3
2
1
1
2
= =
= =

3. The Rule
To change a mixed number to an
improper fraction:
Step one
Multiply the whole number
by the denominator.
Step two
Add this to the numerator.
Step three
Write this answer as the new
numerator. The denominator stays the
same.

4. Worked Example
4
7
=
25
7
3 × 7 = 21
3
21 + 4 = 25

5. Mixed Numbers
Shade the fraction diagrams to represent the mixed numbers and write them as improper
fractions.
1) 5
2) 2
3) 3
4) 2
5) a) 1 b) 4 c) 7 d) 3
1
2
1
7
2
5
3
4
1
6
2
3
3
8
9
10
= 11
2
= 15
7
= 17
5
= 11
4
= 7
6
= 14
3
= 59
8
= 39
10

6. In this fraction subtraction, both the fractions have the
same denominator.
- =
To solve the calculation, the denominator stays the
same, and the numerators are subtracted.
Same Denominators

7. Denominator Multiples
-
x 2 = 10
x 2 = 6
= - = =
Let’s try this with another calculation where the fractions have different
denominators which are multiples of the same number.

8. Denominator Multiples
Let’s try this with another calculation where the fractions have different
denominators which are multiples of the same number.
-
x 5 = 25
x 5 = 10
= - = = 2

9. Subtracting Mixed Numeral Fractions
-
5 3
First, we need to get the common denominators
5 = 5
3 = 3

10. Subtracting Mixed Numeral Fractions
Now we can subtract the fractions
= 2
-
5 3 Simplify
The answer is 2

11. Subtracting Mixed Numeral Fractions
-
8 2
First, we need to get the common denominators
8 = 8
2 = 3

12. Subtracting Mixed Numeral Fractions
-
8 3
8 = 7 +
8 = 7 + + = 7
= 4
-
7 3

13. Subtracting Mixed Numeral Fractions
-
4 1 =
-
5 3 =
-
7 4 =

14. Subtracting Mixed Numeral Fractions
4 1
- = 3
-
4 1 =

15. Subtracting Mixed Numeral Fractions
5 3
- =
5 = 4 + + = 4
-
5 3 =
4 3
- = 1

16. Subtracting Mixed Numeral Fractions
-
7 4 =
7 4
- =
7 = 6 + + = 6
6 4
- = 2 = 2