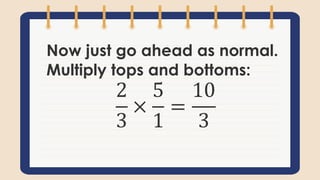
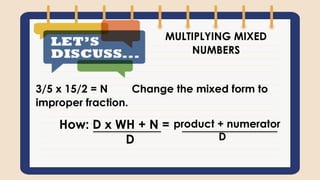
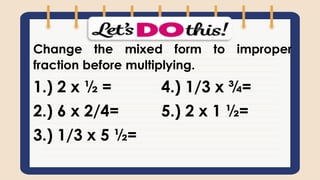This document contains a lesson on multiplying simple fractions. It begins with an opening song about mathematics. It then states that the objective is to multiply simple fractions. It provides the steps to multiply fractions by multiplying the numerators and denominators. It provides examples like 1/2 x 2/5. It discusses how to multiply a fraction by a whole number by writing the whole number as a fraction over 1. Word problems are provided for students to solve. Assessment questions are included at the end to check student understanding of multiplying fractions.

2. OPENING SONG: Mathematics
(To the tune of “Are You Seeping”)
Mathematics (2x)
How it thrills (2x)
It is so exciting
And so
interesting
I love Math (2x)
Mathematics (2x)
Challenging (2x)
Numbers are ideas
Numerals are
symbols
That is Math (2x)

3. Solving Routine Problems
Involving Addition and/or
Subtraction of Fractions Using
Appropriate Problem-solving
Strategies and Tools.
1

4. Solves routine problems involving
addition and/or subtraction of
fractions using appropriate problem-
solving strategies and tools
1

5. How do you change
dissimilar fractions to
similar fractions?
KING BACK
L

6. How do you spend
your Saturday and
Sunday?

7. Let’s talk about Lito and find out
what he does. Listen carefully
and find the good trait of Lito. Do
you possess the same trait? Give
some activities that you do at
home.

8. Lito spends 1 ¼ hours
gardening and 1 ¼ hours
cleaning the yard on Saturday
and Sunday. How many hours
of the day does he spend
profitably?

9. 1.) What are the things you must look for in
a problem before solving it?
2.) What is asked in the problem?
3.) What facts are given?
4.) What operation are we going to use to
solve the problem?
5.) Solve the problem. Show your solution.

10. SOLVING ROUTINE
PROBLEMS INVOLVING
ADDITION and/or
SUBTRACTION OF
FRACTIONS
STEPS:
1. Understand the problem
a. Know what is being asked
b. Know the given facts

11. STEPS:
2. Plan
a. determine the operation/s
needed
3. Solve (Show the solution to the
problem)

12. STEPS:
4. Check and look back
a. check if the answer is
reasonable
b. state the complete
answer

13. Solve for the following:
James spent
𝟑
𝟏𝟎
of his baon for
snacks and 5/10 in buying for
lunch. What part of his baon was
left?

14. Solve for the following:
1.) Cristy finished her assignment in
Mathematics 1 2/8 hours and her
assignment in English for 5/8 hours.
How long did it take her to finish the
two assignments?

15. Solve for the following:
2.) During a contest, Arman
drank 1 9/5 liters of lemonade
and Frank drank 1 ½ liters. Who
drank more lemonade and by
how many liters?

16. Solve for the following:
1.) Aling Minerva, a fish vendor, had
24 ½ kg of fish when she started
peddling. After an hour, she sold 8 ¼
kgs. Three hours later, she sold another
14 ¼ kgs. How many kilograms of fish
were unsold?

17. Solve for the following:
2.) Julie has 1 2/5 meters of
ribbon. She used ½ meter for
the project. How many meters
of ribbon were left?

18. Solve for the following:
3.) Glen has a roll of rope
measuring 36 5/6 meters. If he
gave 10 ½ to Alvin and 18 ¾
meters to Ramon, how many
meters of rope remained to Glen?

19. Solve for the following:
1. Dolor had 4 ½ boxes of
books. She unpacked 2 ½ of
the boxes. How many more
does she need to unpack?

20. Solve for the following:
2. Luis ate 2 ½ guavas and
Eduardo ate 1 ¼ guavas. How
many guavas in all were eaten?
Who ate more? By how much?

21. What have you learned?
How do you solve
routine problems
involving addition
and/or subtraction
of fractions?

22. What have you learned?
Solve the following using the problem-
solving strategies understand, plan, solve
and check.
ASSESSMENT
1. Romel bought 7 ½ kg of butter. He
used 2 3/8 kg of it for baking cakes
and 2 ¼ kg for baking cookies. How
much butter were left?

23. 1. Romel bought 7 ½ kg of butter. He
used 2 3/8 kg of it for baking cakes
and 2 ¼ kg for baking cookies. How
much butter were left?
a. Understand
1. Question asked
2. Information given
b. Plan
1. Fundamental operation/s needed
2. Strategy to use- Block Model
c. Solution

24. Solve the following using the problem-
solving strategies understand, plan, solve
and check.
Margie is baking some doughnuts. She
needs 5 ¼ cups of flour. She has 1 ½ cups
in her jar. How much flour does she need
to buy?
ASSIGNMENT

26. OPENING SONG: Mathematics
(To the tune of “Are You Seeping”)
Mathematics (2x)
How it thrills (2x)
It is so exciting
And so
interesting
I love Math (2x)
Mathematics (2x)
Challenging (2x)
Numbers are ideas
Numerals are
symbols
That is Math (2x)

27. Solving Non-Routine Problems
Involving Addition and/or
Subtraction of Fractions Using
Appropriate Problem-solving
Strategies and Tools.
2

28. Solves non-routine problems
involving addition and/or subtraction
of fractions using appropriate
problem-solving strategies and tools
2

29. What are the steps in solving
routine problems involving
addition/subtraction of
fractions?
KING BACK
L

30. What do you usually do
during your free time? (Wait
for some responses). I have
here some story problems
about how some children
spend their free time.

31. Norma spends her free time playing the
piano. Each day she spends ¾ hour.
When a visitor came in, she has already
played for ¼ hour. To complete her
schedule, how much longer does she
need to play?

32. 1.) How does Norma spend her
free time? Why do you have to
use your free time wisely?
2.) What information are
needed to solve the problem?

33. 3.) What are you asked to
find?
4.) What operation is
needed?

34. 5.) Write the mathematical
sentence.
6.) The final answer is _____.

35. STEPS:
1. Understand the problem
a. Know what is being asked
b. Know the given facts
SOLVING NON-ROUTINE
PROBLEMS INVOLVING
ADDITION and/or
SUBTRACTION OF
FRACTIONS

36. STEPS:
2. Plan
a. determine the operation/s
needed
3. Solve (Show the solution to the
problem)

37. STEPS:
4. Check and look back
a. check if the answer is
reasonable
b. state the complete
answer

38. Solve for the following:
Antonio spent 3/10 hour
changing the tires of his
bicycle. Then he spent 1/5-
hour pumping air into the tires.
How many hours did he spend
fixing his bicycle?

39. Solve for the following:
1.) Luis rides his bicycle ½ km to
school, ¾ km to a ball
field, and 7/10 km home. How far
did he ride in all?

40. Solve for the following:
2.) Steve ran for 7/8 hour and
walked for ½ hour to practice
for a race. How much longer
did he run than walk?

41. Solve for the following:
1.) Nadia prepared 4 1/3 liters of buko
juice and 4 4/5 liters of calamansi
juice to sell one Saturday. How many
liters of juice did she prepare? How
much more calamansi juice did she
prepare than buko juice?

42. Solve for the following:
2.) Mr. Solis needs 12 5/6 meters of wire to
make a pen for his ducks and 10 ¼
meters of wire for his roosters. How many
meters of wire does he need in all? Which
need more wire, the pen for the duck or
for the roosters? By how many meters?

43. Solve for the following:
1. Chamie wants to cover the shelves of her CD
and cassette holder. She measured the
length as follows: CD holder-3/4 meter and
cassette holder is 3/5 meter.
a. What is the total length?
b. What is their difference in length?

44. What have you learned?
How do you solve
non-routine problems
involving addition
and/or subtraction of
fractions?

45. What have you learned?
Solve the following using the problem-
solving strategies understand, plan, solve
and check.
ASSESSMENT
1. A group of girl scouts joined a hiking trip. They
hiked for 2 ½ hours, then rode a banca for ¾
hour, hiked again for 1 1/5 hours, and finally
reached their destination.

46. a.) To find the total time spent for
hiking, what will you do?
b. Solve it. Label your answer.
c. In which activity did they spend
more time? By how many hours?

47. Solve the following using the problem-
solving strategies understand, plan, solve
and check.
In baking, Margie also needs 3 ¼ cups of
milk and 1 ½ cups of honey. What is the
total amount of liquid she needs? Which
is more? By how much?
ASSIGNMENT

49. OPENING SONG: Mathematics
(To the tune of “Are You Seeping”)
Mathematics (2x)
How it thrills (2x)
It is so exciting
And so
interesting
I love Math (2x)
Mathematics (2x)
Challenging (2x)
Numbers are ideas
Numerals are
symbols
That is Math (2x)

50. The Rhyme
"Multiplying fractions: no big problem,
Top times top over bottom times
bottom.
"And don't forget to simplify,
Before it's time to say goodbye"

51. Multiplying
Simple Fractions
3

52. Multiplies simple fractions.
3

53. Change the following mixed numbers to
improper fractions.
1) 9 4/5
2.) 12 3/7
3.) 18 ½
4.) 21 ¾
5.) 25 5/6
KING BACK
L

55. Mang Emong
harvests crates of
mangoes each day.
The table shows the
record of his
harvest.

56. How many crates of
mangoes can Mang
Emong harvest in half
an hour? In 4 hours? In
4 12 hours?
What operation can
we use in solving the
problem?

57. STEPS:
1. Multiply the top numbers
(the numerators).
2. Multiply the bottom numbers
(the denominators).
3. Simplify the fraction if needed.
MULTIPLYING SIMPLE
FRACTIONS

58. Example:
1/2 × 2/5
Step 1. Multiply the top numbers:
1/2 × 2/5 = 1 × 2 = 2
MULTIPLYING SIMPLE
FRACTIONS

59. Example:
1/2 × 2/5
Step 2. Multiply the bottom numbers:
1/2 × 2/5 = 1 × 2/2 × 5 = 2/10
MULTIPLYING SIMPLE
FRACTIONS

60. Fractions and Whole Numbers
Make the whole number a
fraction, by putting it over 1
Example:
Make 5 into
5
1
:=
𝟐
𝟑
× 𝟓
𝟐
𝟑
×
𝟓
𝟏

61. Now just go ahead as normal.
Multiply tops and bottoms:
2
3
×
5
1
=
10
3

62. Solve the following. Write the answer
in simplest form, whenever possible.
1) Multiply 1/3 by 3/5 .
2) What is 4/5 of 1/8 ?
3) Find the product of 1/3 x 1/2 x 3/5 .

63. Solve for the following. Write the
answer in simplest form, whenever
possible.
1) 5/14 x 2/7
2) 2/9 x 7/8
3) What is 12 of 9/13 ?

64. Solve for the following. Write the
answer in simplest form, whenever
possible.
4) What is the product of 4 and
3/25?
5) What is 3/4 x 1/2?

65. Read, analyze, and solve the
problem below.
Mang Jess used 1/4 liters of paint to
cover 1/2 square meters of wall.
How many liters of paint is needed
to cover 2 square meters of wall?

66. What have you learned?
How do we
multiply simple
fractions?

67. What have you learned?
Write the answer in simplest form,
whenever possible.
1) If you multiply 5/6 and 4/5, what
will you get?
2) Find the value of N in the
statement:
4/7 x 3/5 = N
ASSESSMENT

68. What have you learned?
3) If 2/9 x 5/8 are multiplied, the
product is _____.
4.)What is 4/5 of 10/12?
5.) What is ¼ of ¾?
ASSESSMENT

69. Solve the following:
1. 1/2 x 2/5 4. ¾ x 5/6
2. 1/3 x 9/16 5. 5/12 x 4/9
3. 5/8 x 4/5
ASSIGNMENT

71. OPENING SONG: Mathematics
(To the tune of “Are You Seeping”)
Mathematics (2x)
How it thrills (2x)
It is so exciting
And so
interesting
I love Math (2x)
Mathematics (2x)
Challenging (2x)
Numbers are ideas
Numerals are
symbols
That is Math (2x)

72. The Rhyme
"Multiplying fractions: no big problem,
Top times top over bottom times
bottom.
"And don't forget to simplify,
Before it's time to say goodbye"

73. Multiplying
Mixed Fractions
4

74. Multiplies mixed fractions.
4

75. What are the steps in multiplying
simple fractions?
How do you change a whole
number to fraction?
KING BACK
L

76. Anselmo harvested 7 ½
kilograms of pechay from
his vegetable garden. He
sold 3/5 of it in the market
and the rest in the
neighborhood. How many
kilograms were sold in the
market?

77. How many kilograms
were sold in the
market?
MATHEMATICAL SENTENCE:
3/5 of 7 ½ =3/5 x 7 ½ =N

78. MULTIPLYING MIXED
NUMBERS
3/5 x 15/2 = N Change the mixed form to
improper fraction.
How: D x WH + N =
D
product + numerator
D

79. MULTIPLYING MIXED
NUMBERS
𝟑
𝟓
×
𝟏𝟓
𝟐
= 𝑵
𝟑 × 𝟑
𝟏 × 𝟐
=
𝟗
𝟐
1
3
Get the GCF of any of
the numerator and
denominator. Simplify
by cancellation.

80. Multiply the numerator by the numerator,
the denominator by the denominator.
𝟗
𝟐
= 𝟒
𝟏
𝟐
Express the product in simplest
forms.
N=4 ½ kg of pechay were sold in the
market
Label your final answer.

81. Change the mixed form to improper
fraction before multiplying.
1.) 2 x ½ = 4.) 1/3 x ¾=
2.) 6 x 2/4= 5.) 2 x 1 ½=
3.) 1/3 x 5 ½=

82. Express the whole number and mixed
number to improper fraction before
multiplying. Reduce the product in simplest
form.
1.) 15 x 3 3/5 4.) 5 ½ x 2/6 x 8
2.) 4 2/4 x 2/9 5.) 3 1/8 x 2 4/5
3.) 3 1/5 x 3 ¾

83. Solve the problem. Label your
final answers.
1.) Find the area of a room 5 1/3
meters long and 3 ¾ meters
wide.

84. 2.) Mother had 1 ½ dozen
eggs in the refrigerator. She
used 1/3 of the eggs. What
part of the eggs was used?

85. What have you learned?
How do we multiply
mixed
numbers/fractions?
Whole numbers by
mixed numbers?

86. What have you learned?
Find the product. Write the answer in
simplest form.
1. What is 2/3 of 36? 4. 1/3 x 2 ¼
2. What is 5/8 of 48? 5. 2 3/16 x 4/7
3. What is ¾ of 30?
ASSESSMENT

87. Answer Part B=Give the
value of N on page 10 of
your Module.
ASSIGNMENT