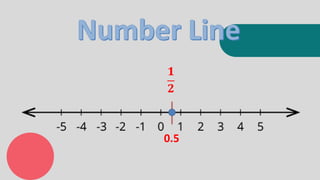
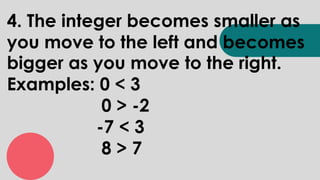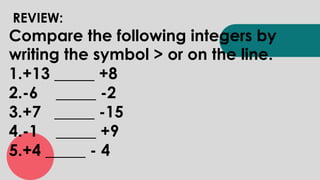The document discusses objectives related to integers, including describing the set of integers and identifying real-life situations involving integers. It then provides information about why we cook food, including making it look appetizing, softening tough foods, and killing microbes. Finally, it discusses integers through examples like representing situations with integers, comparing integers, and adding integers.

3. Objectives:
* Describe the set of Integers
(M6NS-IIg-151)
*Identify real-life situations that
make use of integers
(MGNS-IIg-150)

4. WHY WE COOK THE FOOD WE EAT
We cook our food for three reasons-to make food look more appetizing,
to soften hard and tough foods and to kill any microbe that may happen to
be in the food.
There are many ways of preparing food. Food can be fried, boiled,
broiled, roasted, baked, steamed, stewed or sauteed. They can be well-
cooked or half-cooked.
It is easier to digest food that is well-cooked. But there are foods that are
easier to digest when half-cooked than when well-cooked. Meat and liver
for example, are easier to digest when half-cooked. But certainly, they taste
better when well-cooked.
Many vegetables are also easier to digest when well-cooked, but some
are eaten raw. Lettuce is an example of a vegetable which is eaten raw.

5. REVIEW:
Compare the following quantities by writing
<or >.
1.P2500.00 pesos savings ___ P1240.00 pesos
savings.
2.½ meter of cloth_____ 2 meters of clothes.
Arrange the numbers according to values.
Start from the one that is closest to zero.
1. 2, ¾, 1, 0.5, 7
2. ½, 3, 6, 2/5, 0.75

6. A. Teacher does the following actions
and volunteers do the opposite
actions.
a) walk forward
b) sit down
c) laugh
d) look to the ceiling
e) frown

7. B. Teacher gives the following words,
and the class gives the antonyms.
a) love
b) good
c) clean
d) high
e) happiness

8. If words and actions have opposites,
numbers also have opposites.

9. The set of integers are the set of numbers
consisting of zero (0), the numbers to the right of
zero (positive integers), and the numbers to the
right of zero (negative integers). A positive
integer may be written with or without the plus
sign and a negative integer with minus sign. This
is why integers are also called signed numbers.
Zero (0) is not written with any sign because it is
neutral, meaning, it is neither positive nor
negative.

10. Name an integer for each.
1. 5 units right of 6
2. 8 units left of -1
3. 6 units right of -2
4. 10 units left of 4
5. 20 ft. below sea level
Let's Try

11. PAIR-SHARE
Represent the following with integers.
1. A 30 degrees drop in temperature.
2. A P500 deposit into a bank
account.
3. A weight loss of 5 kilograms.
4. 5 points given to positive behavior
5. 4 calories burned after an exercise.

12. SEAT WORK
Write the integers for each.
1. withdrew P2500
2. 12 steps forward
3. gained 7 kilos
4. 6 floors up
5. 𝟏𝟐𝟎
C below 𝟎𝟎
C

13. Nuggets of Thought
How can we describe
the set of integers
using a number line?

14. ASSESSMENT
A.Describe the following set of integers.
Write positive or negative integers.
1.Moving 5 steps forward
2.Going 3 km upstream
3.Going down 3 km downstream
4.Losing weight of 3 kg.
5.Depositing 1000 pesos

15. ASSIGNMENT
Give the opposite of the following:
1. 5
2. -75
3. -10
4. 90
5. 60

17. Objectives:
*Comparing Integers with Other
Numbers Such as Whole Numbers,
Fractions and Decimals
*Comparing and Arranging Integers
from Least to Greatest and Vice Versa

18. WHY WE COOK THE FOOD WE EAT
We cook our food for three reasons-to make food look more appetizing,
to soften hard and tough foods and to kill any microbe that may happen to
be in the food.
There are many ways of preparing food. Food can be fried, boiled,
broiled, roasted, baked, steamed, stewed or sauteed. They can be well-
cooked or half-cooked.
It is easier to digest food that is well-cooked. But there are foods that are
easier to digest when half-cooked than when well-cooked. Meat and liver
for example, are easier to digest when half-cooked. But certainly, they taste
better when well-cooked.
Many vegetables are also easier to digest when well-cooked, but some
are eaten raw. Lettuce is an example of a vegetable which is eaten raw.

19. REVIEW:
Illustrate the following on a number line.
1. The set of integers less than or equal to -3 but
greater than -20.
2. The set of integers less than -1 but greater than -
8.
3. The set of integers greater than -6 but less than 0.
4. The set of integers less than 8 but greater than 2.
5. The set of integers greater than -7 but less than 7.

20. USING THE NUMBER LINE
Answer the following questions:
1. What are the numbers to the right of
zero? Are they greater than zero?
2. What are the numbers to the left of zero?
Are they less than zero?
3. Can we say that 10 is greater than -10?

21. In comparing integers, we use the
following symbols:
>, <, =

22. *Zero is greater than all negative integers
but smaller than all positive integers.
*All positive integers are
greater than all negative integers; all
negative integers are less than all positive
integers.
*When comparing 2 integers with the
same signs, that one that is farther to the
right on the number line is the greater
integer.

23. On a number line, the number located to
the right is greater than the number to its
left.
Consider the following examples:
1. Zero is located to the left of positive
integers. Therefore, zero is smaller than all
positive integers.
Examples:
0 < 1 0 < 3 0 < 5

24. 2. Zero is located to the right of negative
numbers. Therefore, zero is greater than all
negative integers.
Examples:
0 > -1 0 > -3 0 > -5
3. All positive integers are located to the right of
negative numbers. Therefore, all positive
numbers are greater than all negative integers.
Examples:
1 > -1 1> -3 1 > -5

25. 4. The integer becomes smaller as
you move to the left and becomes
bigger as you move to the right.
Examples: 0 < 3
0 > -2
-7 < 3
8 > 7

26. 𝟏
𝟐
0.5

27. Write true if the statement is correct
and false if not.
____1.
1
2
> 2
____2. 8 < -12
____3. -3 > -5
____4. 0.5 > 0
____5. -14 > -9
Let's Try

28. PAIR-SHARE
Arrange the following integers from the
least to the greatest and greatest to the
least.
1.) 2, -6, - 8, 5, -1, 7, -5
2.) 25, -20, 18, 15, -15
3.) 40, 41, -20, 25, 30
4.) 40, 50, -40, -50, 10
5.) 0, -4, 4, -2, 7, 10

29. Nuggets of Thought
How will you compare integers?
How will you arrange integers from
the least to the greatest or
greatest to the least?

30. ASSESSMENT
Arrange the following integers from the
least to the greatest.
1.-3, -8, 0, -5, 9, 6
2.-2, 5. 7, -8, -1, -5
3.-11, -5, 8, -1, -5
4.15, -9, 12, -17, -8, 3
5.13, 0, -13, 17, -8, 3

31. ASSIGNMENT
Write > or < to make ach statement
true.
1. -5 ____ 0
2. 9____ -8
3. -7 ____ 7
4. 55 ____ -75
5. -32 ____ -24

33. Objectives:
*Performing Addition of Integers
*Solving Routine and Non-routine
Problems Involving Addition of
Integers

34. WHY WE COOK THE FOOD WE EAT
We cook our food for three reasons-to make food look more appetizing,
to soften hard and tough foods and to kill any microbe that may happen to
be in the food.
There are many ways of preparing food. Food can be fried, boiled,
broiled, roasted, baked, steamed, stewed or sauteed. They can be well-
cooked or half-cooked.
It is easier to digest food that is well-cooked. But there are foods that are
easier to digest when half-cooked than when well-cooked. Meat and liver
for example, are easier to digest when half-cooked. But certainly, they taste
better when well-cooked.
Many vegetables are also easier to digest when well-cooked, but some
are eaten raw. Lettuce is an example of a vegetable which is eaten raw.

35. REVIEW:
Compare the following integers by
writing the symbol > or on the line.
1.+13 _____ +8
2.-6 _____ -2
3.+7 _____ -15
4.-1 _____ +9
5.+4 _____ - 4

36. PROBLEM OPENER
Mrs. Reyes bought fruits that cost P 700.00 from
a wholesaler and sold them in her fruits stand.
On Monday, her sales are P800.00 and on
Tuesday, P500.00. But on Wednesday, she loses
P400.00 because some of the fruits are already
rotten. Considering the sales of fruits for the
three days, did Mrs. Reyes gain or lose profit?

37. Considering the sales of Mrs. Reyes on three
days, represent the gain and loss using
integers. To determine the total sales means to
combine the gains and loss.
How are we going to combine the gain and
loss?
What is the total sale of fruits of Mrs. Reyes?
How can we determine if Mrs. Reyes gained or
lost money from selling her fruits?

38. Determine how to combine integers
by studying the given examples
below:
1.( +4 ) + ( +3)= ( +7)
2.(-4) + ( -3)= ( -7)

39. To add integers having the same sign, add the integers then affix
the common sign.
To add integers having different sign, subtract their distances from
zero then affix the sign of the addend with the longer distance
away from zero.
Examples:
1. 5 + 8 = 13
2. (-12) + (-15) = (-27)
3. 56 + (-12) = 44
4. (-63) + 49 = (-14)
5. (-47) + (-35) = (-82)

40. PAIR-SHARE
Answer the following:
1.1. ( -21) + (+5)
2.(+47) + (+16)
3.(-72) + (- 38)
4.(-10) + (+87)
5. (+15) + (-56) + (-9)

41. SEAT WORK
Use the 4-Step Plan in solving the
problem.
Mt. Everest, the highest elevation in
Asia, is 29 029 feet above sea level.
The dead sea, the lowest elevation, is
1 412 feet below sea level. What is the
sum of these two elevations?

42. Nuggets of Thought
How do we add integers with the
same signs?
How do we add integers with
different signs?

43. ASSESSMENT
Add the following integers.
1.(-25) + (+17)
2.(+73) + (-29)
3.(-89) + ( -103)
4.(+ 194) + (+57)
5. (-217) + ( +104)

44. ASSIGNMENT
Solve the problem.
1.Kris gets on the elevator on the
eleventh floor. The elevator goes
down two floors and stops. It then
continues to go down four more floors
where Kris got off. In what floor did she
get off the elevator?