Dokumen ini membahas penggunaan konsep limit fungsi dalam pemecahan masalah matematika, dengan fokus pada mahasiswa kelas XI. Standar kompetensi mencakup pemahaman limit di titik terhingga dan tak terhingga serta penghitungan bentuk tak tentu. Selain itu, dokumen menjelaskan penerapan limit dalam konteks kehidupan melalui contoh dan grafik untuk mendekati solusi.

2. Matematika
SMA
( Semester Genap )
Sasaran : Kelas XI
Durasi Sajian: 3 x 45 Menit
Topik Bahasan
Penggunaan Konsep Limit
Fungsi dalam Pemecahan
Masalah

3.  Menggunakan konsep limit fungsi dan turunan fungsi
dalam pemecahan masalah.
Standar Kompetensi
 Menjelaskan secara intuitif arti limit fungsi di suatu titik
terhingga dan tak terhingga;
 Menggunakan sifat limit fungsi untuk menghitung
bentuk tak tentu fungsi aljabar dan trigonometri.
Kompetensi Dasar

4.  Dapat menjelaskan arti limit fungsi di suatu titik
terhingga dan tak terhingga;
 Dapat menghitung limit fungsi aljabar dan trigonometri;
 Dapat menggunakan sifat limit fungsi untuk menghitung
bentuk tak tentu limit fungsi aljabar dan trigonometri.
Tujuan Pembelajaran

5.  Penting untuk bernalar matematis;
 Sangat membantu dalam memahami bidang
kajian lain seperti fisika, kimia, biologi, teknik,
ekonomi, dan lain-lain.
Mengapa
Belajar Limit
?

7. Amati arah terbang dua ekor burung
menuju sangkar dari arah yang
berbeda.
Jika kita aplikasikan dalam bentuk
matematis (kalkulus) maka:
Tiang sangkar sebagai garis x = c;
Jejak terbang burung identik dengan
grafik fungsi y = f(x);
Jarak kedua ekor burung semakin
dekat ke sangkar atau mendekati c;
Ketinggian burung pada saat tiba
dalam sangkar misalkan L;
X
L
y =
f(x)
x=
c
L
)
x
(
f
lim
c
x
=

Ditulis
:

8. L
)
x
(
f
lim
c
x
=

L
)
x
(
f
lim
dan
L
)
x
(
f
lim
L
)
x
(
f
lim
c
x
c
x
c
x
=
=

= +
-



Definisi tersebut mempunyai arti,
bilamana x dekat tetapi berlainan
dengan c maka f(x) dekat ke L.
Seberapa dekat?
Untuk memperjelas permasalahan ini
perhatikan grafik fungsi f(x) di kolom
sebelah kiri.
0
X
Y
c
L
f(x
)
Jika x mendekati c baik dari kiri
maupun dari kanan maka f(x) akan
semakin mendekati L. Jadi, kita
peroleh:

9. 0
X
Y
3
6
x mendekati 3 dari kiri  x mendekati 3 dari kanan
x 2,5 2,99 2,999 ... 3 ... 3,001 3,01 3,5
f(x) 5,5 5,99 5,999 ... 6 ... 6,001 6,01 6,5
f(x) mendekati 6  f(x) mendekati 6
Penyelesaian:
Fungsi tidak
terdefinisi pada
x = 3, karena diperoleh bentuk (tak
tentu).
Ambil beberapa nilai x yang
mendekati 3 dari kiri maupun dari
kanan.
0
0
3
x
9
x
)
x
(
f
2
-
-
=
Grafik
fungsi 3
x
9
x
)
x
(
f
2
-
-
=
Contoh 1:
Tentukan nilai dari
3
x
9
x
lim
2
3
x -
-

Dengan cara
aljabar:
3
x
)
3
x
)(
3
x
(
lim
3
x
9
x
lim
3
x
2
3
x -
-
+
=
-
-


6
)
3
x
(
lim
3
x
=
+
=


10. 0
X
Y
2
0
4
0
-20
-40
4
2 x mendekati 3 dari kiri  x mendekati 3 dari kanan
x 2 2,99 2,999 ... 3 ... 3,001 3,01 4
f(x) -13 -1794,01 -17994 ... ? ... 18006 1806,01 25
f(x) mendekati bilangan
negatif yang sangat kecil

f(x) mendekati bilangan
positif yang sangat besar
x=3
Asimtot
Tegak
Contoh 2:
Tentukan nilai dari
3
x
9
x
lim
2
3
x -
+

Penyelesaian:
Fungsi tidak
terdefinisi pada
x = 3, karena diperoleh bentuk (tak
tentu).
Lakukan pendekatan seperti pada
contoh 1.
0
0
3
x
9
x
)
x
(
f
2
-
+
=
Grafik
fungsi 3
x
9
x
)
x
(
f
2
-
+
=

11. Dari gambar grafik nampak bahwa
jika x mendekati 3 dari kiri maka f(x)
akan mendekati bilangan negatif tak
hingga.
Sebaliknya jika x mendekati 3 dari
kanan maka f(x) akan mendekati
bilangan positif tak hingga.
Karena
maka nilai dari:
0
X
Y
2
0
4
0
-20
-40
4
2
x=3
Asimtot
Tegak
Grafik
fungsi 3
x
9
x
)
x
(
f
2
-
+
=
-
=
-
+
-
 3
x
9
x
lim
2
3
x
+
=
-
+
+
 3
x
9
x
lim
2
3
x
3
x
9
x
lim
3
x
9
x
lim
2
3
x
2
3
x -
+

-
+
+
-


ada
tidak
3
x
9
x
lim
2
3
x -
+


12. 0
X
Y
+∞
-∞
x mendekati bilangan negatif yang sangat besar x mendekati bilangan positif yang sangat besar
x - ∞ ... -1.000.000 -100.000 -10.000 -1.000 -100 100 1.000 10.000 100.000 1.000.000 ... + ∞
f(x) 0 ... -0,000001 -0,00001 -0,0001 -0,001 -0,01 0,01 0,001 0,0001 0,00001 0,000001 ... 0
f(x) semakin mendekati nol (0) f(x) semakin mendekati nol (0)
Penyelesaian:
Dengan pendekatan nilai x positif
tanpa batas (+∞) dan negatif tanpa
batas (-∞). Lihat tabel dan grafik.
0
x
1
lim
x
=


Kita peroleh nilai:
Contoh 3:
Bagaimana dengan ?
x
1
lim
x 


13. Start
Rasiona
l?
Bagi dengan
pangkat tertinggi
Rasionalkan/
kalikan akar
sekawan
kemudian bagi
pangkat tertinggi
Hasil
Stop
Tida
k
Ya
Flowchart untuk
menghitung nilai:
)
x
(
f
lim
x 

Start
Substitusi x = c
Bentuk
tak
tentu?
Lakukan
pemfaktoran atau
rasionalkan
bentuk akar
Lanjutkan Hitung
Hasil
Stop
Tida
k
Ya
Flowchart untuk
menghitung nilai:
)
x
(
f
lim
c
x

14. Kalikan
akar
sekawan
x
4
2
x
4
2
x
4
2
x
lim
x
4
2
x
lim
0
x
0
x -
+
-
+

-
-
=
-
- 

)
1
x
(
)
1
x
x
)(
1
x
(
lim
1
x
1
x
lim
2
1
x
3
1
x -
+
+
-
=
-
-


Contoh 4:
Tentukan nilai dari:
a)
b)
c)
d)
Penyelesaian:
Untuk soal (a) dan (b) jika dilakukan
substitusi akan diperoleh bentuk tak
tentu
Sehingg
a,
a) Lakukan
pemfaktoran
b) Rasionalkan bentuk
akar
1
x
x
lim 2
1
x
+
+
=

3
1
1
12
=
+
+
=
0
0
3
1
x
1
x
lim
3
1
x
=
-
-

1
x
1
x
lim
3
1
x -
-

x
4
2
x
lim
0
x -
-

3
x
x
2
1
x
4
x
3
lim 2
2
x +
-
-
+


)
x
4
(
x
4
2
x
4
2
4
)
x
4
2
(
x
lim
0
x -
-
-
-
-
+
-
+
=

x
)
x
4
2
(
x
lim
x
4
4
)
x
4
2
(
x
lim
0
x
0
x
-
+
=
+
-
-
+
=


4
0
4
2
x
4
2
lim
0
x
=
-
+
=
-
+
=

4
x
4
2
x
lim
0
x
=
-
-

)
x
4
x
x
(
lim 2
x
+
-



15. Kalikan akar
sekawan
2
2
2
2
2
2
2
2
x
3
x
x
x
x
2
x
1
x
x
4
x
x
3
x
2
2
x
lim
3
x
x
2
1
x
4
x
3
lim
+
-
-
+
=
+
-
-
+




Karena fungsi rasional maka
langsung bagi pangkat tertinggi
)
x
( 2
c) adalah fungsi
rasional.
Mengapa
?
2
2
x
3
x
1
x
1
x
4
x 2
3
lim
+
-
-
+
=


2
3
0
0
2
0
0
3
=
+
-
-
+
=
3
x
x
2
1
x
4
x
3
lim 2
2
x +
-
-
+


2
3
3
x
x
2
1
x
4
x
3
lim 2
2
x
=
+
-
-
+


Rasionalkan dengan cara kalikan akar
sekawan, selanjutnya bagi pangkat
tertinggi.
d) bukan fungsi
rasional.
Mengapa
?
)
x
4
x
x
(
lim 2
x
+
-


L
=
+
-


)
x
4
x
x
(
lim 2
x
x
4
x
x
x
4
x
x
)
x
4
x
x
(
lim 2
2
2
x +
+
+
+

+
-
=


x
4
x
x
)
x
4
x
(
x
lim 2
2
2
x +
+
+
-
=

 x
4
x
x
x
4
lim 2
x +
+
-
=


2
0
1
1
4
-
=
+
+
-
=
2
)
x
4
x
x
(
lim 2
x
-
=
+
-


x
4
x
x
x
4
x
x
x
x
x
x
4
x 1
1
4
lim
lim
2
2
2
+
+
-
=
+
+
-
=





16. 
Andaikan n bilangan bulat positif, k
konstanta, f dan g adalah fungsi yang
mempunyai limit di c, maka:






diman
a:
; utk n
genap

k
k
lim
c
x
=

)
c
(
f
)
x
(
f
lim
c
x
=

  )
x
(
g
lim
)
x
(
f
lim
)
x
(
g
)
x
(
f
lim
c
x
c
x
c
x 



=

  )
x
(
g
lim
)
x
(
f
lim
)
x
(
g
)
x
(
f
lim
c
x
c
x
c
x 



=

)
x
(
f
lim
k
)
x
(
kf
lim
c
x
c
x 

=
0
)
x
(
g
lim
;
)
x
(
g
lim
)
x
(
f
lim
)
x
(
g
)
x
(
f
lim
c
x
c
x
c
x
c
x

=










n
c
x
n
c
x
))
x
(
f
lim
(
))
x
(
f
(
lim


=
n
c
x
n
c
x
)
x
(
f
lim
)
x
(
f
lim


=
Kita lihat contoh penerapannya!
0
)
x
(
f
lim
c
x



17. 4
lim
x
lim
7
1
x
1
x 

-
=
4
lim
x
7
lim
1
x
1
x 

-
=
Contoh 5:
Tentukan nilai dari:
a)
b)
Penyelesaian:
a) )
4
x
7
(
lim
1
x
-

4
)
1
(
7 -
=
3
=








+
-
+
 1
x
2
2
x
3
x
lim 2
2
2
x
  )
x
(
g
lim
)
x
(
f
lim
)
x
(
g
)
x
(
f
lim
c
x
c
x
c
x 



=

)
x
(
f
lim
k
)
x
(
kf
lim
c
x
c
x 

=
)
4
x
7
(
lim
1
x
-


18. 1
x
2
lim
)
2
x
3
x
(
lim
2
2
x
2
2
x
+
-
+
=


)
1
x
2
(
lim
2
lim
x
3
lim
x
lim
2
2
x
2
x
2
x
2
2
x
+
-
+
=




b) 







+
-
+
 1
x
2
2
x
3
x
lim 2
2
2
x
1
lim
x
2
lim
2
lim
x
3
lim
x
lim
2
x
2
2
x
2
x
2
x
2
2
x





+
-
+
=
1
)
2
(
2
2
)
2
(
3
2
2
2
+
-
+
=
1
8
2
6
4
+
-
+
=
3
8
=
  )
x
(
g
lim
)
x
(
f
lim
)
x
(
g
)
x
(
f
lim
c
x
c
x
c
x 



=

Teorema

Teorema

Teorema

0
)
x
(
g
lim
;
)
x
(
g
lim
)
x
(
f
lim
)
x
(
g
)
x
(
f
lim
c
x
c
x
c
x
c
x

=










n
c
x
n
c
x
)
x
(
f
lim
)
x
(
f
lim


=

19. Beberapa sifat yang sering dipakai:






Bukti untuk sifat

x
O
1
A
B
C
D
X
Y
∆OAB dan ∆OCB adalah segitiga
siku-siku.
OB
AB
x
sin
AB
1
AB
=

=
x
sin =
x
BD
busur
Panjang =
OB
BC
x
tan
BC
1
BC
=

=
x
tan =
1
x
x
sin
lim
0
x
=

1
x
x
cos
lim
0
x
=

1
x
x
tan
lim
0
x
=

1
x
sin
x
lim
0
x
=

0
x
cos
x
lim
0
x
=

1
x
tan
x
lim
0
x
=

(I) Misalkan:
jari-jari lingkaran ( r ) = 1 satuan
panjang, BOA = x
2
x
0 p
<
<

20. Bukti untuk sifat

x
O
1
A
B
C
D
X
Y AB < BD < BC  sin x < x
< tan x
(dibagi sin
x)
1
x
x
sin
x
cos
x
cos
1
x
sin
x
1 <
<

<
<
karen
a:
(II) Untuk maka
0
x
2
<
<
p
-
2
x
0
p
<
-
<
1
x
x
sin
x
cos <
< 1
x
x
sin
x
cos <
-
-
<
-




-
=
-
=
-
x
sin
x
sin
x
cos
x
cos
1
x
x
sin
x
cos <
-
-
<
 1
x
x
sin
x
cos <
<

∆OAB dan ∆OCB adalah segitiga
siku-siku.
OB
AB
x
sin
AB
1
AB
=

=
x
sin =
x
BD
busur
Panjang =
OB
BC
x
tan
BC
1
BC
=

=
x
tan =
(I) Misalkan:
jari-jari lingkaran ( r ) = 1 satuan
panjang, BOA = x
2
x
0 p
<
<
Dari bentuk (I) dan (II)
maka:
1
lim
x
x
sin
lim
x
cos
lim
0
x
0
x
0
x 


<
<
;
2
x
2
p
<
<
p
-
1
x
x
sin
x
cos <
<
1
x
x
sin
lim
0
x
=

1
0
cos
x
cos
lim
0
x
=
=

1
1
lim
0
x
=


21. 2
3
x
3
x
3
sin
lim
x
2
x
3
sin
lim
0
x
0
x

=


2
2
0
x
2
0
x x
)
x
sin
2
1
(
1
lim
x
x
2
cos
1
lim
-
-
=
-


Contoh 6:
Tentukan nilai dari:
a)
b)
Penyelesaian:
a)
x
2
x
3
sin
lim
0
x
2
0
x x
x
2
cos
1
lim
-

b)
x
3
x
3
sin
lim
2
3
0
x
=
1
2
3

=
2
3
=
2
2
0
x x
x
sin
2
lim

=
2
2
0
x x
x
sin
lim
2

=
2
0
x x
x
sin
lim
2 





=

2
1
2
=
2
=
2
x
x
2
cos
1
lim 2
0
x
=
-

2
3
x
2
x
3
sin
lim
0
x
=


22. “Klik pada tombol untuk memilih soal”

23. 1. ....
1
x
1
x
lim
2
1
x
=
+
-
-

1
x
)
1
x
)(
1
x
(
lim
1
x
1
x
lim
1
x
2
1
x +
-
+
=
+
-
-

-

)
1
x
(
lim
1
x
-
=
-

1
1-
-
=
2
-
=
2
1
x
1
x
lim
2
1
x
-
=
+
-
-

2

0
2
-
1
-
Klikpada pilihan (a - e) untukmemilihjawaban

24. 2.
3
4
....
2
x
6
x
x
lim
2
2
x
=
-
-
+

2
x
)
3
x
)(
2
x
(
lim
2
x
6
x
x
lim
2
x
2
2
x -
+
-
=
-
-
+


)
3
x
(
lim
2
x
+
=

3
2+
=
5
=
5
2
x
6
x
x
lim
2
2
x
=
-
-
+

2
5
6
Klikpada pilihan(a - e) untukmemilihjawaban

25. Rasionalk
an bentuk
akar
4
x
4
x
4
x
16
x
lim
4
x
16
x
lim
2
4
x
2
4
x -
-

-
-
=
-
-


3.
3
4
-
0
3
-
....
4
x
16
x
lim
2
4
x
=
-
-

4
x
4
x
)
16
x
(
lim
2
4
x -
-
-
=

4
x
4
x
)
4
x
)(
4
x
(
lim
4
x -
-
-
+
=

4
x
)
4
x
(
lim
4
x
-
+
=

4
4
)
4
4
( -
+
=
0
8
=
0
=
0
4
x
16
x
lim
2
4
x
=
-
-

4
Klikpada pilihan (a - e) untukmemilihjawaban

26. Kalikan akar
sekawan
x
1
x
1
x
1
x
1
x
x
1
x
1
lim
0
x -
+
+
-
+
+

-
-
+
=

)
x
1
x
1
(
x
x
2
lim
0
x -
+
+
=

4.
2
-
1
1
-
....
x
x
1
x
1
lim
0
x
=
-
-
+

....
x
x
1
x
1
lim
0
x
=
-
-
+

)
x
1
x
1
(
x
)
x
1
(
)
x
1
(
lim
0
x -
+
+
-
-
+
=

x
1
x
1
2
lim
0
x -
+
+
=

1
2
2
0
1
0
1
2
=
=
-
+
+
=
1
x
x
1
x
1
lim
0
x
=
-
-
+

3
-
0
Klikpada pilihan (a - e) untukmemilihjawaban

27. Kalikan akar
sekawan
x
h
x
x
h
x
h
x
h
x
lim
0
h +
+
+
+

-
+
=

5. ....
h
x
h
x
lim
0
h
=
-
+

....
h
x
h
x
lim
0
h
=
-
+

)
x
h
x
(
h
x
)
h
x
(
lim
0
h +
+
-
+
=

)
x
h
x
(
h
h
lim
0
h +
+
=

x
h
x
1
lim
0
h +
+
=

x
2
1
x
x
1
x
0
x
1
=
+
=
+
+
=
x
2
1
h
x
h
x
lim
0
h
=
-
+

x
3
1
x
3
2
x
2
x
2
x
2
1
Klikpada pilihan(a - e) untukmemilihjawaban

28. )
x
sin
x
)(cos
x
sin
x
(cos
x
sin
x
cos
lim
4
x -
+
-
= p

6. ....
x
2
cos
x
sin
x
cos
lim
4
x
=
-
p

x
sin
x
cos
x
sin
x
cos
lim
x
2
cos
x
sin
x
cos
lim 2
2
x
x 4
4 -
-
=
-
p
p 

x
sin
x
cos
1
lim
4
x +
= p

4
4 sin
cos
1
p
p +
=
2
2
1
2
1
2
1 +
=
2
1
=
2
1
x
2
cos
x
sin
x
cos
lim
4
x
=
-
p

3
2
1
2
1
3
2
1
2
3
Klikpada pilihan (a - e) untukmemilihjawaban

29. 7.
5
5
-
3
-





 

=

 3
5
x
3
sin
x
3
x
5
x
5
tan
lim
x
3
sin
x
5
tan
lim
0
x
0
x





 
=
 x
3
sin
x
3
x
5
x
5
tan
lim
3
5
0
x
1
1
3
5


=
3
5
=
3
5
x
3
sin
x
5
tan
lim
0
x
=

....
x
3
sin
x
5
tan
lim
0
x
=

3
5
-
3
5
Klikpada pilihan(a - e) untukmemilihjawaban

30. 8.
12
....
x
tan
x
2
sin
lim
2
1
3
3
0
x
=
 3
2
1
0
x
2
1
3
3
0
x x
tan
x
2
sin
lim
x
tan
x
2
sin
lim 







=


3
2
1
2
1
0
x
4
x
tan
x
x
2
x
2
sin
lim 









=

3
2
1
2
1
0
x
3
x
tan
x
x
2
x
2
sin
lim
4 








=

3
)
1
1
(
64 
=
64
=
64
x
tan
x
2
sin
lim
2
1
3
3
0
x
=

64
32
10
37
Klikpada pilihan(a - e) untukmemilihjawaban

31. 9.
0
....
x
sin
x
x
cos
1
lim
0
x
=
-

2
1
x
sin
x
x
cos
1
lim
0
x
=
-

2
1
1
1
1
1
12
=
+


=
x
cos
1
1
x
sin
x
x
x
sin
lim
2
0
x +








=









+
=
 )
x
cos
1
(
x
sin
x
x
sin
lim
2
0
x








+
-
=
 )
x
cos
1
(
x
sin
x
x
cos
1
lim
2
0
x






+
+

-
=
-

 x
cos
1
x
cos
1
x
sin
x
x
cos
1
lim
x
sin
x
x
cos
1
lim
0
x
0
x
1
2
4
1
2
1








+


=
 x
cos
1
1
x
sin
x
x
x
sin
lim 2
2
0
x
Klikpada pilihan(a - e) untukmemilihjawaban

32. 10
.
3
-
1
-
....
x
2
x
3
x
x
6
sin
)
1
x
(
lim 2
3
2
0
x
=
+
+
-

)
x
2
x
)(
1
x
(
x
6
sin
)
1
x
)(
1
x
(
lim
x
2
x
3
x
x
6
sin
)
1
x
(
lim 2
0
x
2
3
2
0
x +
+
-
+
=
+
+
-


x
2
x
x
6
sin
)
1
x
(
lim 2
0
x +
-
=

1
2
0
)
1
0
(
6

+
-
=
1
2
6

-
=
3
-
=
3
x
2
x
3
x
x
6
sin
)
1
x
(
lim 2
3
2
0
x
-
=
+
+
-

8
-
5
-
6
-
x
6
x
6
sin
2
x
)
1
x
(
6
lim
0
x

+
-
=

Klikpada pilihan(a - e) untukmemilihjawaban

33. Bagi pangkat
tertinggi
x
x
x
x
3
x
x
x
x
3
x
2
2
2
lim
+
+
=


Kalikan akar
sekawan
x
x
3
x
x
x
3
x
)
x
x
3
x
(
lim 2
2
2
x +
+
+
+

-
+
=


1. ....
)
x
x
3
x
(
lim 2
x
=
-
+


....
)
x
x
3
x
(
lim 2
x
=
-
+


x
x
3
x
x
x
3
x
lim 2
2
2
x +
+
-
+
=


x
x
3
x
x
3
lim 2
x +
+
=


1
1
3
lim
x
3
x +
+
=


2
3
1
0
1
3
=
+
+
=
2
3
)
x
x
3
x
(
lim 2
x
=
-
+


4
7
3
7
3
4
2
3
3
2
Klikpada pilihan(a - e) untukmemilihjawaban

34. Kalikan akar
sekawan
x
2
x
x
4
x
x
2
x
x
4
x
)
x
2
x
x
4
x
(
lim 2
2
2
2
2
2
x +
+
-
+
+
-

+
-
-
=


Bagi pangkat
tertinggi
2.
2
-
1
-
....
)
x
2
x
x
4
x
(
lim 2
2
x
=
+
-
-

 ....
)
x
2
x
x
4
x
(
lim 2
2
x
=
+
-
-


x
2
x
x
4
x
)
x
2
x
(
)
x
4
x
(
lim 2
2
2
2
x +
+
-
+
-
-
=


x
2
x
x
4
x
x
6
lim 2
2
x +
+
-
-
=


2
2
2
2
2
2
x
x
2
x
x
x
x
4
x
x
x
x
6
x
lim
+
+
-
=
-


x
2
x
4
x 1
1
6
lim
+
+
-
-
=


3
2
6
0
1
0
1
6
-
=
-
=
+
+
-
-
=
3
)
x
2
x
x
4
x
(
lim 2
2
x
-
=
+
-
-


6
-
4
-
3
-
Klikpada pilihan (a - e) untukmemilihjawaban

35. Bagi pangkat
tertinggi
Kalikan akar
sekawan
3. ....
)
x
1
x
(
x
lim 2
x
=
-
+

 ....
)
x
1
x
(
x
lim 2
x
=
-
+


x
1
x
x
1
x
)
x
1
x
(
x
lim 2
2
2
x +
+
+
+

-
+
=


x
1
x
)
x
1
x
(
x
lim 2
2
2
x +
+
-
+
=


x
1
x
x
lim 2
x +
+
=


x
x
x
1
x
x
x
x
x
2
2
2
lim
+
+
=


1
1
1
lim
2
x
1
x +
+
=


2
1
1
0
1
1
=
+
+
=
2
1
)
x
1
x
(
x
lim 2
x
=
-
+


0
2
4
1
2
1
3
1
Klikpada pilihan (a - e) untukmemilihjawaban

36. Bagi pangkat
tertinggi
4.
2

3
....
1
x
x
2
1
x
x
3
lim
x
=






+
-
-


....
1
x
x
2
1
x
x
3
lim
x
=






+
-
-


)
1
x
)(
1
x
(
)
1
x
(
x
2
)
1
x
(
x
3
lim
x +
-
-
-
+
=


1
x
x
2
x
2
x
3
x
3
lim 2
2
2
x -
+
-
+
=


1
x
x
5
x
lim 2
2
x -
+
=


2
2
2
2
2
2
x
1
x
x
x
x
5
x
x
x
lim
-
+
=


1
0
1
0
1
1
1
lim
2
x
1
x
5
x
=
-
+
=
-
+
=


1
1
x
x
2
1
x
x
3
lim
x
=






+
-
-


1
9
Klikpada pilihan(a - e) untukmemilihjawaban

37. Bagi pangkat
tertinggi
....
2
x
x
x
6
x
2
x
3
lim 2
3
3
4
x
=
+
-
+
+
-


4
4
4
2
4
3
4
4
3
4
4
x
2
x
x
x
x
x
x
x
6
x
x
2
x
x
3
x
lim
+
-
+
+
-
=


4
3
2
4
x
2
x
1
x
1
x
1
x
6
x
2
x
3
lim
+
-
+
+
-
=


0
0
0
0
0
0
3
+
-
+
+
-
=

=
=
0
3
ada)
(tidak
2
x
x
x
6
x
2
x
3
lim 2
3
3
4
x +
-
+
+
-


5.
0
2
-
1
-
3
-

....
2
x
x
x
6
x
2
x
3
lim 2
3
3
4
x
=
+
-
+
+
-


Klikpada pilihan(a - e) untukmemilihjawaban

38. 1.
Jik
a
buktikan bahwa nilai
dari
x
1
x
x
1
lim
y
2
0
x
-
+
+
=

x
1
x
x
1
lim
y
2
0
x
-
+
+
=

1
x
x
1
1
x
x
1
x
1
x
x
1
lim 2
2
2
0
x +
+
+
+
+
+

-
+
+
=

)
1
x
x
1
(
x
1
x
x
1
lim 2
2
0
x +
+
+
-
+
+
=

)
1
x
x
1
(
x
)
x
1
(
x
lim 2
0
x +
+
+
+
=

1
x
x
1
x
1
lim 2
0
x +
+
+
+
=

2
1
1
0
0
1
0
1
2
=
+
+
+
+
=
2
1
y=
1
x
tan
x
2
sin
x
cos
x
2
sin
lim
x
cos
x
sin
3
)
y
(
x 2
2
1
=
+
+
-


39. 1.
Jik
a
buktikan bahwa nilai
dari
x
1
x
x
1
lim
y
2
0
x
-
+
+
=

x
cos
x
sin
3
)
y
(
x 2
2
1
x
tan
x
2
sin
x
cos
x
2
sin
lim
+
+
-

1
x
tan
x
2
sin
x
cos
x
2
sin
lim
x
cos
x
sin
3
)
y
(
x 2
2
1
=
+
+
-

x
cos
x
sin
3
0
x 2
x
tan
x
2
sin
x
cos
x
2
sin
lim
+
+
=

)
1
(
x
tan
)
x
cos
1
(
x
2
sin
lim
x
cos
3
0
x +
+
=

x
cos
3
0
x
0
x
0
x 1
x
cos
1
lim
x
tan
x
lim
x
2
x
2
sin
lim
2
+
+



=



1
4
2
2
1
0
cos
1
1
1
2
0
cos
3
=

=
+
+



=

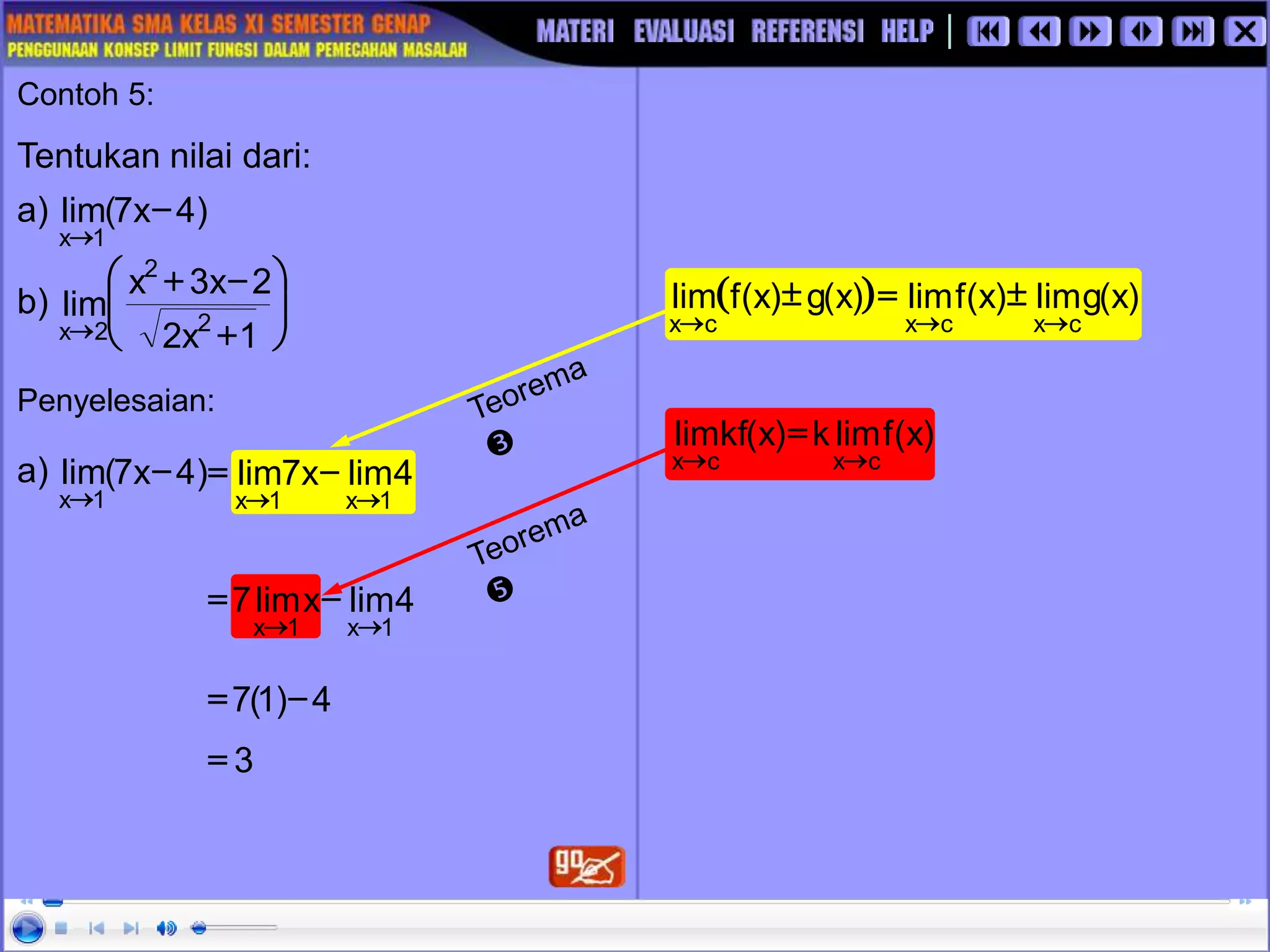
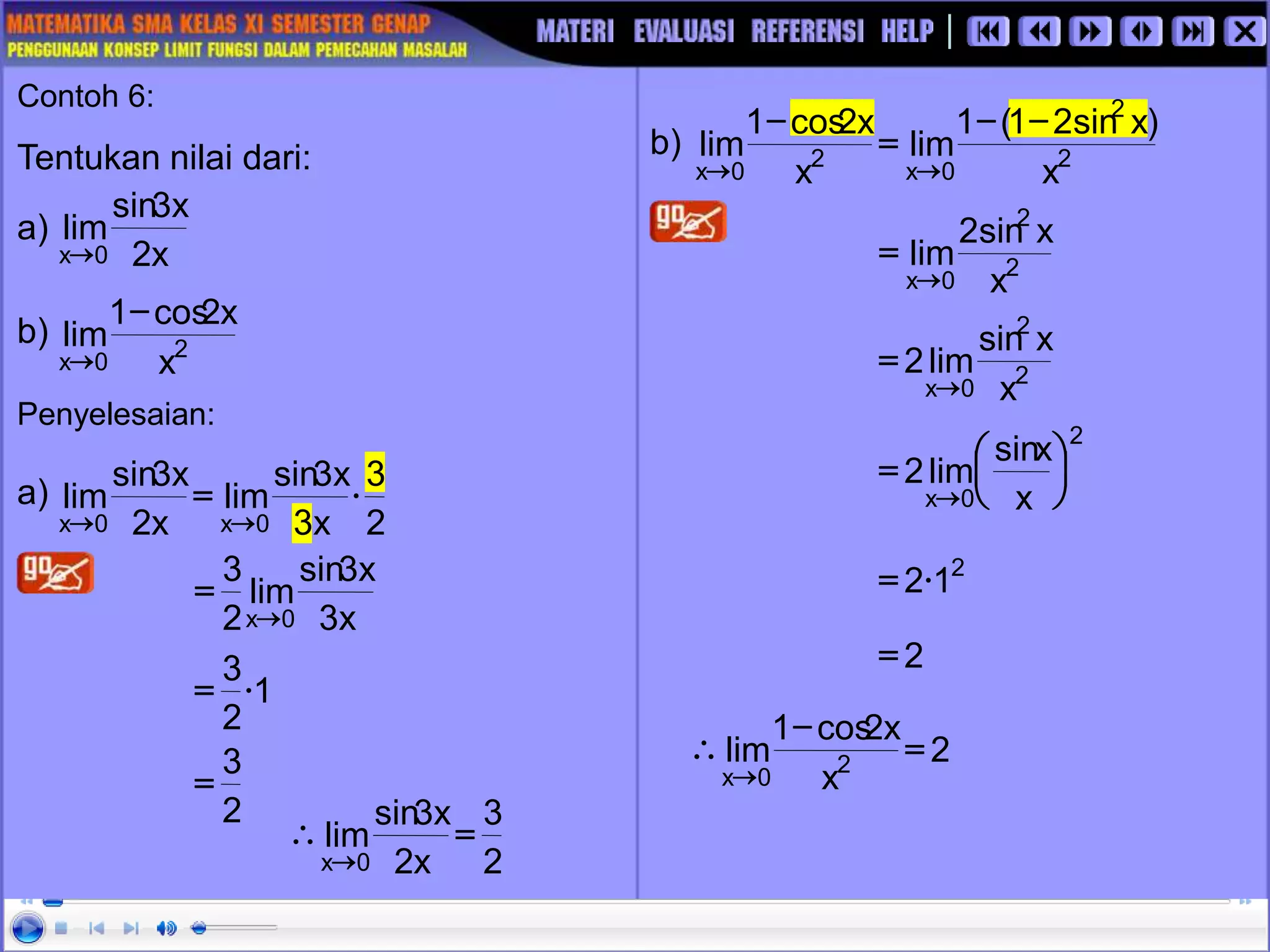
40. 1. Dengan menggunakan teorema
limit hitunglah nilai dari:
a.
....
x
3
x
2
1
x
3
2
lim
2
x
=





 +
-
+






 +
-






+
=

 x
3
x
2
lim
1
x
3
2
lim
2
x
2
x
x
lim
3
x
2
lim
1
x
3
lim
2
lim
2
x
2
x
2
x
2
x




+
-
+
=
2
3
)
2
(
2
1
)
2
(
3
2 +
-
+
=
14
45
2
7
7
2
-
=
-
=
14
45
x
3
x
2
1
x
3
2
lim
2
x
-
=





 +
-
+

1a
.





 +
-
+
 x
3
x
2
1
x
3
2
lim
2
x
b.
2. Jika dan
buktikan dengan teorema limit
bahwa:
1
)
x
(
g
lim
c
x
-
=

3
)
x
(
f
lim
c
x
=

a.
b.
c.
)
5
x
2
)(
4
x
(
lim
5
x
-
+

10
)
x
(
g
)
x
(
f
lim 2
2
c
x
=
+

[ ] 3
)
x
(
g
)
c
x
(
)
x
(
f
lim
c
x
=
-
+

[ ] 6
3
)
x
(
f
)
x
(
g
lim3
c
x
-
=
+


41. ....
)
5
x
2
)(
4
x
(
lim
5
x
=
-
+

)
5
x
2
(
lim
)
4
x
(
lim
5
x
5
x
-

+
=


)
5
lim
x
2
lim
(
)
4
lim
x
lim
(
5
x
5
x
5
x
5
x 



-

+
=
)
5
5
2
(
)
4
5
( -


+
=
5
9
=
45
=
45
)
5
x
2
)(
4
x
(
lim
5
x
=
-
+

1b
.
1. Dengan menggunakan teorema
limit hitunglah nilai dari:
a. 




 +
-
+
 x
3
x
2
1
x
3
2
lim
2
x
b.
2. Jika dan
buktikan dengan teorema limit
bahwa:
1
)
x
(
g
lim
c
x
-
=

3
)
x
(
f
lim
c
x
=

a.
b.
c.
)
5
x
2
)(
4
x
(
lim
5
x
-
+

10
)
x
(
g
)
x
(
f
lim 2
2
c
x
=
+

[ ] 3
)
x
(
g
)
c
x
(
)
x
(
f
lim
c
x
=
-
+

[ ] 6
3
)
x
(
f
)
x
(
g
lim3
c
x
-
=
+


42. Bukti
:
2a
.
(terbukt
i)
....
)
x
(
g
)
x
(
f
lim 2
2
c
x
=
+

)
x
(
g
lim
)
x
(
f
lim 2
c
x
2
c
x 

+
=
2
c
x
2
c
x
)]
x
(
g
lim
[
)]
x
(
f
lim
[


+
=
2
2
]
1
[
3 -
+
=
1
9+
=
10
=
10
)
x
(
g
)
x
(
f
lim 2
2
c
x
=
+

1. Dengan menggunakan teorema
limit hitunglah nilai dari:
a. 




 +
-
+
 x
3
x
2
1
x
3
2
lim
2
x
b.
2. Jika dan
buktikan dengan teorema limit
bahwa:
1
)
x
(
g
lim
c
x
-
=

3
)
x
(
f
lim
c
x
=

a.
b.
c.
)
5
x
2
)(
4
x
(
lim
5
x
-
+

10
)
x
(
g
)
x
(
f
lim 2
2
c
x
=
+

[ ] 3
)
x
(
g
)
c
x
(
)
x
(
f
lim
c
x
=
-
+

[ ] 6
3
)
x
(
f
)
x
(
g
lim3
c
x
-
=
+


43. Bukti
:
2b
.
(terbukt
i)
[ ] ....
)
x
(
g
)
c
x
(
)
x
(
f
lim
c
x
=
-
+

)
x
(
g
lim
)
c
x
(
lim
)
x
(
f
lim
c
x
c
x
c
x 



-
+
=
)
1
(
)
c
c
(
3 -

-
+
=
)
1
(
0
3 -

+
=
3
=
[ ] 3
)
x
(
g
)
c
x
(
)
x
(
f
lim
c
x
=
-
+

1. Dengan menggunakan teorema
limit hitunglah nilai dari:
a. 




 +
-
+
 x
3
x
2
1
x
3
2
lim
2
x
b.
2. Jika dan
buktikan dengan teorema limit
bahwa:
1
)
x
(
g
lim
c
x
-
=

3
)
x
(
f
lim
c
x
=

a.
b.
c.
)
5
x
2
)(
4
x
(
lim
5
x
-
+

10
)
x
(
g
)
x
(
f
lim 2
2
c
x
=
+

[ ] 3
)
x
(
g
)
c
x
(
)
x
(
f
lim
c
x
=
-
+

[ ] 6
3
)
x
(
f
)
x
(
g
lim3
c
x
-
=
+


44. Bukti
:
2c
.
(terbukt
i)
[ ] ....
3
)
x
(
f
)
x
(
g
lim3
c
x
=
+

[ ]
3
)
x
(
f
lim
)
x
(
g
lim
c
x
3
c
x
+

=







 +

=



3
lim
)
x
(
f
lim
)
x
(
g
lim
c
x
c
x
3
c
x
[ ]
3
3
1
3 +

-
=
[ ]
6
1
-
=
6
-
=
[ ] 6
3
)
x
(
f
)
x
(
g
lim3
c
x
-
=
+

1. Dengan menggunakan teorema
limit hitunglah nilai dari:
a. 




 +
-
+
 x
3
x
2
1
x
3
2
lim
2
x
b.
2. Jika dan
buktikan dengan teorema limit
bahwa:
1
)
x
(
g
lim
c
x
-
=

3
)
x
(
f
lim
c
x
=

a.
b.
c.
)
5
x
2
)(
4
x
(
lim
5
x
-
+

10
)
x
(
g
)
x
(
f
lim 2
2
c
x
=
+

[ ] 3
)
x
(
g
)
c
x
(
)
x
(
f
lim
c
x
=
-
+

[ ] 6
3
)
x
(
f
)
x
(
g
lim3
c
x
-
=
+


45. 3. Berat dalam gram dari suatu tumor
yang membahayakan pada saat t
adalah w(t)=0,1t2—0,05t; t diukur
dalam minggu. Berapa laju
pertumbuhan tumor jika t = 10
minggu?
2. Sebuah perusahaan dalam waktu t
tahun memperoleh keuntungan
total sebesar L(t)=1500t2 dollar.
Berapa laju keuntungan sesaat
(keuntungan marjinal) saat t = 5?
1. Sebuah benda bergerak selama t
detik menempuh jarak s meter,
ditentukan dengan rumus s(t)=t2+2.
Tentukan kecepatan sesaat pada t
= 4.
1. Jarak: s(t)= t2+2. Maka kecepatan
sesaat pada t = 4 adalah:
Jadi, kecepatan sesaat benda
adalah: 8 m/detik
Gunakan
rumus:
untuk menyelesaikan permasalahan
berikut.
h
)
t
(
f
)
h
t
(
f
lim
0
h
-
+

h
]
2
4
[
]
2
)
h
4
[(
lim
2
2
0
h
+
-
+
+
=

h
]
2
16
[
]
2
h
h
8
16
[
lim
2
0
h
+
-
+
+
+
=

h
18
18
h
8
h
lim
2
0
h
-
+
+
=

h
)
8
h
(
h
lim
h
h
8
h
lim
0
h
2
0
h
+
=
+
=


8
)
8
h
(
lim
0
h
=
+
=


46. 2. Total untung: L(t)=1500t2. Maka
keuntungan marjinal untuk t = 5
adalah:
Jadi, keuntungan marjinal
perusahaan: 15000 dollar/tahun.
h
]
)
5
(
1500
[
]
)
h
5
(
1500
[
lim
2
2
0
h
-
+
=

h
)]
25
(
1500
[
)]
h
h
10
25
(
1500
[
lim
2
0
h
-
+
+
=

h
]
37500
[
]
h
1500
h
15000
37500
[
lim
2
0
h
-
+
+
=

h
h
15000
h
1500
lim
2
0
h
+
=

h
)
15000
h
1500
(
h
lim
0
h
+
=

15000
)
15000
h
1500
(
lim
0
h
=
+
=

3. Berat dalam gram dari suatu tumor
yang membahayakan pada saat t
adalah w(t)=0,1t2—0,05t; t diukur
dalam minggu. Berapa laju
pertumbuhan tumor jika t = 10
minggu?
2. Sebuah perusahaan dalam waktu t
tahun memperoleh keuntungan
total sebesar L(t)=1500t2 dollar.
Berapa laju keuntungan sesaat
(keuntungan marjinal) saat t = 5?
1. Sebuah benda bergerak selama t
detik menempuh jarak s meter,
ditentukan dengan rumus s(t)=t2+2.
Tentukan kecepatan sesaat pada t
= 4.
Gunakan
rumus:
untuk menyelesaikan permasalahan
berikut.
h
)
t
(
f
)
h
t
(
f
lim
0
h
-
+


47. 3. Berat tumor: w(t)=0,1t2—0,05t.
Maka laju pertumbuhan tumor
untuk t = 10 adalah:
Jadi, laju pertumbuhan tumor
adalah:
1,95 gram/minggu.
h
)]
10
(
05
,
0
)
10
(
1
,
0
[
)]
h
10
(
05
,
0
)
h
10
(
1
,
0
[
lim
2
2
0
h
-
-
+
-
+
=

h
]
5
,
0
)
100
(
1
,
0
[
]
h
05
,
0
5
,
0
)
h
h
20
100
(
1
,
0
[
lim
2
0
h
-
-
-
-
+
+
=

h
5
,
0
10
h
05
,
0
5
,
0
h
1
,
0
h
2
10
lim
2
0
h
+
-
-
-
+
+
=

h
)
95
,
1
h
1
,
0
(
h
lim
h
h
95
,
1
h
1
,
0
lim
0
h
2
0
h
+
=
+
=


95
,
1
95
,
1
)
0
(
1
,
0
)
95
,
1
h
1
,
0
(
lim
0
h
=
+
=
+
=

3. Berat dalam gram dari suatu tumor
yang membahayakan pada saat t
adalah w(t)=0,1t2—0,05t; t diukur
dalam minggu. Berapa laju
pertumbuhan tumor jika t = 10
minggu?
2. Sebuah perusahaan dalam waktu t
tahun memperoleh keuntungan
total sebesar L(t)=1500t2 dollar.
Berapa laju keuntungan sesaat
(keuntungan marjinal) saat t = 5?
1. Sebuah benda bergerak selama t
detik menempuh jarak s meter,
ditentukan dengan rumus s(t)=t2+2.
Tentukan kecepatan sesaat pada t
= 4.
Gunakan
rumus:
untuk menyelesaikan permasalahan
berikut.
h
)
t
(
f
)
h
t
(
f
lim
0
h
-
+


48.  Andi Hakim Nasution dkk, Matematika 2, Departemen
Pendidikan dan Kebudayaan, Jakarta, 1994.
 Bernard V. Zandy dan Jonathan J. White,
CliffsQuickReviewTM Calculus, Pakar Raya, Bandung,
2004.
 B.K. Noormandiri, Buku Pelajaran Matematika SMA,
Jilid 2A, Erlangga, Jakarta, 2004.
 Edwin J. Purcell dan Dale Varberg, Kalkulus dan
Geometri Analitis, Jilid 1, Erlangga, Jakarta, 1990.
 http://www.answer.com/topik/limit-of-a-function.
 http://www.garizhdizain.com.

49. terima kasih, kami
sampaikan kepada mereka
yang telah berkontribusi
dalam pembuatan
multimedia pembelajaran
ini