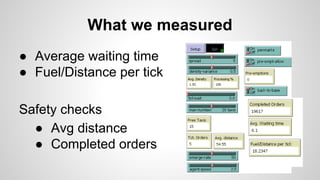
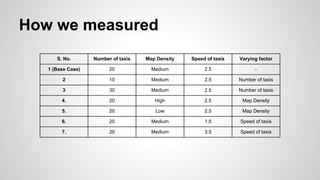
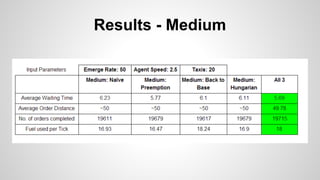
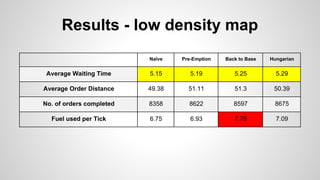
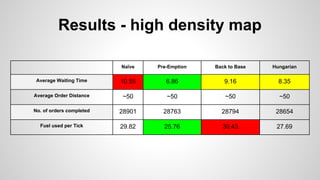
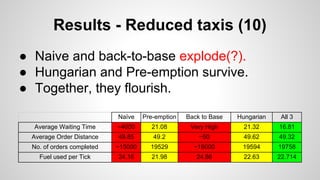
The document discusses a simulation for optimizing taxi service operations to minimize average waiting time in urban environments with varying densities. It presents multiple strategies, including greedy algorithms and predictive methods, and evaluates their performance through simulations using NetLogo. Results indicate that preemptive strategies consistently outperform others, especially under conditions of reduced resources and high demand.

1. Taxi service simulation to
minimize waiting time
Aditya Gupta (2011009)
Sushant Mehta (2010088)
Mayank Verma (2010048)
Group 7

2. Introduction
● Problem
● Solutions
● Simulation
● Result

3. Problem
We run a taxi service in cities of varying
density.
Pickup requests emerge dynamically (in time).
We must deploy limited taxis in realtime to
minimize average pickup time.

4. Sound familiar?
● Dynamic Task Allocation Problem
○ N cabs from {10, 20, 30}
■ Varying speed
○ Dynamic Pickup+Drop Requests
■ Emerge anywhere
■ Emerge anytime
■ Can have any distance
○ Stochastic environment
■ Eased density maps

5. Solutions
● Assign the every new request the nearest
free taxi?
● Assign every free taxi the nearest possible
request?

6. Solutions
● Assign the every new request the nearest
free taxi? Greedy.
● Assign every free taxi the nearest possible
request? Also Greedy. Pre-Emptive. Stable
Matching. Futuristic (Queueing with cost).
Costly? Try to achieve perfect queues?

7. More cool solutions
● What if I predict where the requests will
come from?
● The optimal static (one-time) allocation.

8. More cool solutions
● What if I predict where the requests will
come from? Simple centralized supervised
learning.
Back-to-base(s) (100). Tradeoff - (hot/far).
● The optimal static (one-time) allocation.
The Hungarian method.

9. Simulation
● NetLogo 5.0
○ ~ 300 lines
● Map generation
● 4 solutions
○ Naive
○ Pre-emptive
○ Back-to-base
○ Hungarian
■ Java Extension

10. Some snaps and Demo

11. Hungarian Method
● Combinatorial
optimization
algorithm
● Running time O(n3
)
● Extendable to
skewed matrices as
well.

12. What we measured
● Average waiting time
● Fuel/Distance per tick
Safety checks
● Avg distance
● Completed orders

13. How we measured
S. No. Number of taxis Map Density Speed of taxis Varying factor
1 (Base Case) 20 Medium 2.5 -
2 10 Medium 2.5 Number of taxis
3 30 Medium 2.5 Number of taxis
4. 20 High 2.5 Map Density
5. 20 Low 2.5 Map Density
6. 20 Medium 1.5 Speed of taxis
7. 20 Medium 3.5 Speed of taxis

14. Results - Medium

15. Results - low density map
Naïve Pre-Emption Back to Base Hungarian
Average Waiting Time 5.15 5.19 5.25 5.29
Average Order Distance 49.38 51.11 51.3 50.39
No. of orders completed 8358 8622 8597 8675
Fuel used per Tick 6.75 6.93 7.78 7.09

16. Results - high density map
Naïve Pre-Emption Back to Base Hungarian
Average Waiting Time 10.55 6.86 9.16 8.35
Average Order Distance ~50 ~50 ~50 ~50
No. of orders completed 28901 28763 28794 28654
Fuel used per Tick 29.82 25.76 30.43 27.69

17. Results - Reduced taxis (10)
● Naive and back-to-base explode(?).
● Hungarian and Pre-emption survive.
● Together, they flourish.
Naïve Pre-emption Back to Base Hungarian All 3
Average Waiting Time ~4000 21.08 Very High 21.32 16.81
Average Order Distance 49.85 49.2 ~50 49.62 49.32
No. of orders completed ~15000 19529 ~16000 19594 19758
Fuel used per Tick 24.16 21.98 24.86 22.63 22.714

18. Results - Reduced speed
● Just like reduced taxi’s case.
● And we tried many permutations and combinations of these parameters
and strategies.
Naïve Pre-Emption Back to Base Hungarian All 3
264.21 13.19 151.97 18.76 12.81
~50 ~50 ~50 ~50 58.49
19459 19608 19406 19639 19420
29.3 18.51 28.79 21.35 19.6

19. What did we learn?
● Work best together.
○ 16.81 vs 21.08 points in reduced taxis case.
○ 9 ~ 25% better times than Naive.
● Individually, pre-emption!
○ Consistent performer across scenarios.

20. More results
● Efficiency gain apparent in critical application
○ Reduced taxis/resources
○ Reduced speed/efficiency
○ High density maps
● Fuel and pickup time correlated (efficiency)
○ Pre-emption not bad at all
● Back-to-base is a fuel efficiency disaster.

21. Conclusion
● Taxi allocation to minimize avg. pickup time
○ Task allocation problem
● Multiple Strategies
○ Predictive, futuristic, optimal, stable, greedy
● NetLogo simulation
○ Java Extension
● Results and Findings

22. Possible extensions
● Discarding a few orders to further improve
average waiting time
● Adding realistic constraints: roads, traffic etc.
○ Assignment Problem
○ Routing Problem

23. Thanks